22 câu trắc nghiệm Nguyên hàm có đáp án (phần 1) | Toán lớp 12 – Tuyển tập 1000 Bài tập trắc nghiệm Toán 12 Giải tích có đáp án chi tiết đầy đủ các mức độ giúp bạn ôn trắc nghiệm Toán 12 thi Tốt nghiệp THPT.-22 câu trắc nghiệm Nguyên hàm có đáp án (phần 1)
22 câu trắc nghiệm Nguyên hàm có đáp án (phần 1)
Với 22 bài tập & câu hỏi trắc nghiệm Nguyên hàm Toán lớp 12 Giải tích có đáp án và lời giải chi tiết đầy đủ các mức độ nhận biết, thông hiểu, vận dụng sẽ giúp học sinh ôn trắc nghiệm Toán 12.
22 câu trắc nghiệm Nguyên hàm có đáp án (phần 1)
Câu 1: Trong các mệnh đề sau mệnh đề nào nhận giá trị đúng?
A. Hàm số y = 1/x có nguyên hàm trên (-∞; +∞).
B. 3x2 là một số nguyên hàm của x3 trên (-∞; +∞).
C. Hàm số y = |x| có nguyên hàm trên (-∞;+∞).
D. 1/x + C là họ nguyên hàm của lnx trên (0;+∞).
Dựa vào định lí: Mọi hàm số liên tục trên K đều có nguyên
hàm trên K. Vì y = |x| liên tục trên R nên có nguyên hàm trên R .
Phương án A sai vì y=1/x không xác định tại x=0 ∈ (-∞;+∞).
Phương án B sai vì 3x2 là đạo hàm của x3.
Phương án D sai vì 1/x là đạo hàm của lnx trên (0; +∞).
Vậy chọn đáp án C.
Câu 2: Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x-sin2x ?
x2 + (1/2).cos2x B. x2 + cos2 x C. x2 – sin2x D. x2 + cos2x .
Ta có
∫(2x-sin2x)dx=2∫xdx-∫sin2xdx
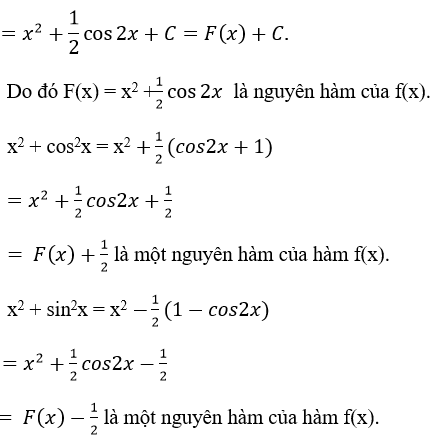
D không phải là nguyên hàm của f(x). Vậy chọn đáp án D.
Câu 3: Tìm nguyên hàm của
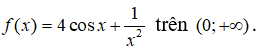
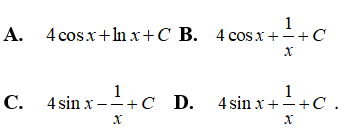
Với x ∈ (0; +∞) ta có
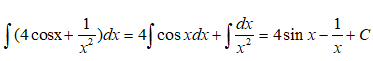
Vậy chọn đáp án C.
Câu 4:
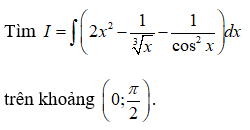
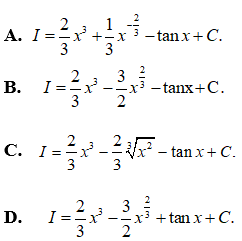
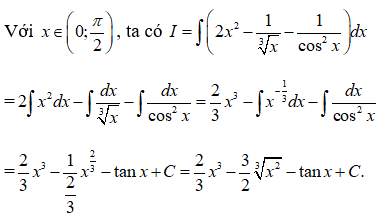
Vậy chọn đáp án B.
Ghi chú. Yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.
Câu 5:
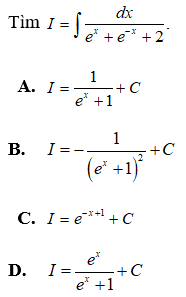
Đặt u = ex + 1 ⇒ u’ = ex. Ta có
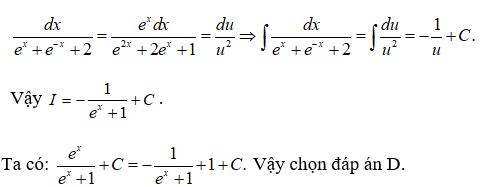
Câu 6: Trong các hàm số sau hàm số nào không phải là một nguyên hàm của f(x) = cosxsinx ?
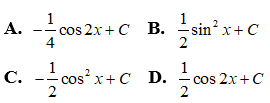
Cách 1.
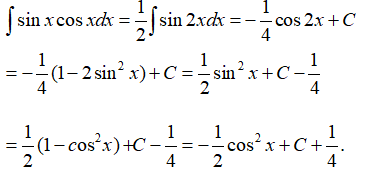
Cách 2. Sử dụng phương pháp biến đổi số ta có:
Đặt u = cosx thì u’ = -sinx và ∫sinxcosxdx = -∫u.u’dx = -∫udu
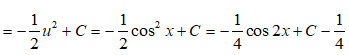
Vậy chọn đáp án D.
Câu 7: Tìm I=∫(3x2 – x + 1)exdx
A. I = (3x2 – 7x +8)ex + C B. I = (3x2 – 7x)ex + C
C. I = (3x2 – 7x +8) + ex + C D. I = (3x2 – 7x + 3)ex + C
Sử dụng phương pháp tính nguyên hàm từng phần ta có:
Đặt u = 3x2 – x + 1 và dv = exdx ta có du = (6x – 1)dx và v = ex . Do đó:
∫(3x2 – x + 1)exdx = (3x2 – x + 1)ex – ∫(6x – 1)exdx
Đặt u1 = 6x – 1; dv1 = exdx Ta có: du1 = 6dx và v1 = ex .
Do đó ∫(6x – 1)exdx = (6x – 1)ex – 6∫exdx = (6x – 1)ex – 6ex + C
Từ đó suy ra
∫(3x2 – x + 1)exdx = (3x2 – x + 1)ex – (6x – 7)ex + C = (3x2 – 7x + 8)ex + C
Vậy chọn đáp án A.
Câu 8:
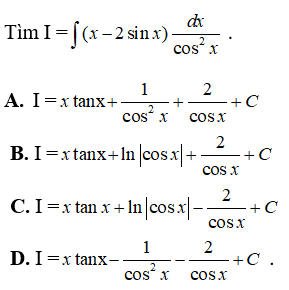
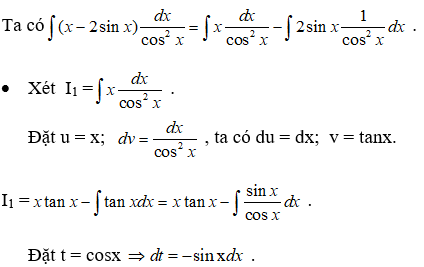
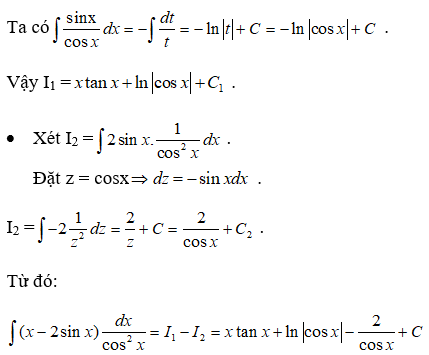
Vậy chọn đáp án C.
Câu 9: Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc
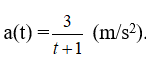
Vận tốc ban đầu của vật là 6m/s. Vận tốc của vật sau 10 giây xấp xỉ bằng
A. 10m/s B. 11m/s C. 12m/s D. 13m/s.
Vận tốc của vật bằng
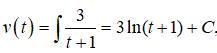
với t = 0 ta có v(0)= C = 6 nên phương trình vận tốc của chuyển động là :
v(t) = 3ln(t + 1) + 6 (m/s)
khi đó v(10) = 3ln11 + 6 ≈ 13 (m/s) .
Vậy chọn đáp án D.
Câu 10: Tìm I = ∫cos(4x + 3)dx .
A. I = sin(4x + 2) + C B. I = – sin(4x + 3) + C
C. I = (1/4).sin(4x + 3) + C D. I = 4sin(4x + 3) + C
Đặt u = 4x + 3
⇒ du = 4dx ⇒ dx = 1/4 du và cos(4x+3)dx được viết thành
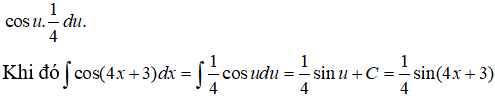
Câu 11: Tìm I = ∫x.e3xdx
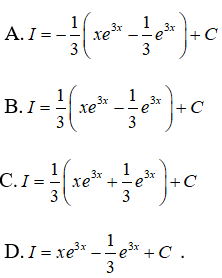
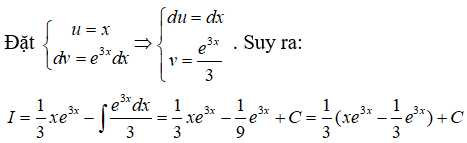
Xem thêm Bài tập trắc nghiệm Toán 12 phần Giải tích ôn thi Tốt nghiệp THPT có đáp án hay khác:


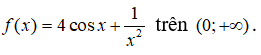
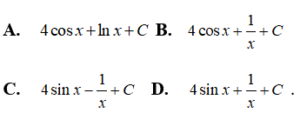

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn