Chứng minh bất đẳng thức bằng Cô-si, Bunhiacopxki

Với Chứng minh bất đẳng thức bằng Cô-si, Bunhiacopxki môn Toán lớp 8 phần Đại số sẽ giúp học sinh ôn tập, củng cố kiến thức từ đó biết cách làm các dạng bài tập Toán lớp 8 Chương 4: Bất phương trình bậc nhất một ẩn để đạt điểm cao trong các bài thi môn Toán 8.

Chứng minh bất đẳng thức bằng Cô-si, Bunhiacopxki

Dạng bài: Sử dụng bất đẳng thức Cô – si, bất đẳng thức Bunhiacopxki

A. Phương pháp giải

a) Bất đẳng thức Cô – si

Cho hai số không âm a, b, ta luôn có:

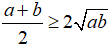
, dấu đẳng thức xảy ra khi và chỉ khi a=b.

Mở rộng:

a. Với các số a, b, c không âm, ta luôn có:

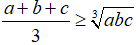
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c.

b. Với n số 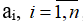 không âm, ta luôn có:

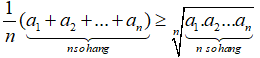
Dấu đẳng thức xảy ra khi và chỉ khi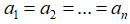

b) Bất đẳng thức Bunhiacopxki

Cho a₁, a₂, b₁, b₂ là những số thực, ta có:

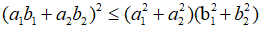
Dấu đẳng thức xảy ra khi 

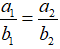
Mở rộng: Với các số thực a₁, a₂, b₁, b₂, a₃, b₃, ta luôn có:

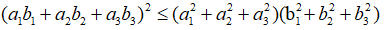
Dấu đẳng thức xảy ra khi 

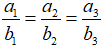
B. Ví dụ minh họa

Câu 1: Cho a,b>0. Chứng minh rằng:

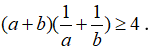
Lời giải:

Sử dụng bất đẳng thức Cô-si:

• Cho cặp số a, b, ta được:

 

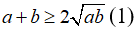
• Cho cặp số 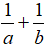, ta được:

     

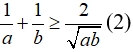
Nhân hai vế tương ứng của (1), (2), ta được:

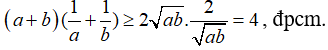
Dấu bằng xảy ra khi: 

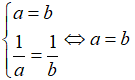
Câu 2: Cho ba số dương a, b, c. Chứng minh rằng:

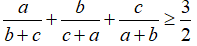
Giải.

Ta có:

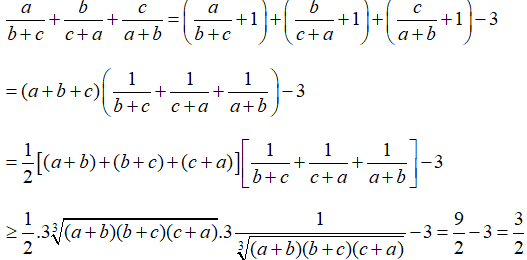
Dấu đẳng thức xảy ra khi:

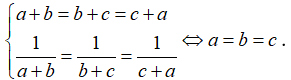
Câu 3: Chứng minh rằng với a, b, c tùy ý ta luôn có:

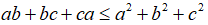
Lời giải:

Ta có:

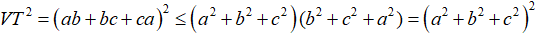
Lấy căn bậc hai của hai vế, ta đi đến:

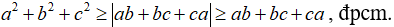
C. Bài tập tự luyện

Câu 1: Cho 3 số dương x, y, z tùy ý. Chứng minh rằng:

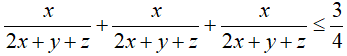
Câu 2: Cho 3 số dương x, y, z thỏa mãn: xyz=1. Chứng minh rằng:

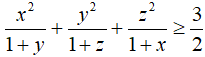
Câu 3: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:

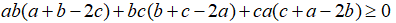
Câu 4: Cho 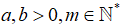. Chứng minh rằng:

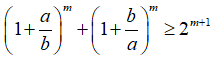
Câu 5: Chứng minh rằng với mọi số thực x, y luôn có:

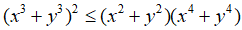
Câu 6: Hai số x, y thỏa mãn 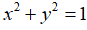. Chứng minh rằng

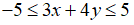
Câu 7: Cho các số không âm a, y thỏa mãn 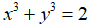. Chứng minh rằng:

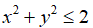
D. Bài tập bổ sung

Bài 1. Cho các số thực dương x, y, z thỏa mãn: x + y + z = 3. Chứng minh rẳng:

xx+2yz+yy+2xz+zz+2xy≥1

Bài 2. Cho các số thực dương x, y, z. Chứng minh rẳng:

x3x+2y+y3y+2z+z3z+2x≥x2+y2+z23

Bài 3. Cho các số thực dương x, y, z. Chứng minh:

x3(2×2+y2)(2×2+z2)+y3(2y2+z2)(2y2+x2)+z3(2z2+x2)(2z2+y2)≤1x+y+z

Bài 4. Cho các số thực dương x, y, z thỏa mãn: xy + yz + zx = 1. Chứng minh rằng:

2xyz(x+y+z)≤59+x4y2+y4z2+z4x2

Bài 5. Cho các số thực dương x, y, z. Chứng minh:

1×2+xy+yz+1y2+yz+zx+1z2+zx+xy≤(x+y+zxy+yz+zx)2

Xem thêm các dạng bài tập Toán lớp 8 chọn lọc hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

---