Công thức, cách tính thể tích Hình lập phương hay, chi tiết – Tổng hợp trên 200 Công thức, Định nghĩa, Định lí môn Toán giúp học sinh nắm vững kiến thức lý thuyết quan trọng, thường gặp để học tốt môn Toán hơn.-Công thức, cách tính thể tích Hình lập phương hay, chi tiết
Công thức, cách tính thể tích Hình lập phương hay, chi tiết
Công thức, cách tính thể tích Hình lập phương hay, chi tiết
1. Thể tích hình lập phương
Quy tắc: Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
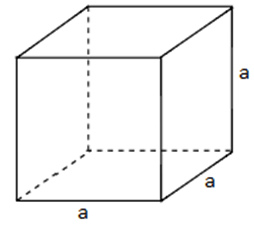
V = a × a × a
2. Một số dạng bài tập
Dạng 1: Tính thể tích hình lập phương khi biết độ dài cạnh
Phương pháp: Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
Ví dụ. Tính thể tích hình lập phương có cạnh 10cm.
Bài giải
Thể tích của hình lập phương là:
10 × 10 × 10 = 1000 (cm3)
Đáp số: 1000cm3
Dạng 2: Tính thể tích hình lập phương khi diện tích xung quanh hoặc diện tích toàn phần
Phương pháp: Tính diện tích một mặt sau đó tìm lập luận để tìm độ dài cạnh.
Ví dụ. Một hộp phấn hình lập phương có diện tích toàn phần là 96cm2. Tính thể tích của hộp phấn đó.
Bài giải
Diện tích một mặt của hình lập phương là:
96 : 6 = 16 (cm2)
Vì 36 = 4 × 4 nên cạnh của hình lập phương là 4cm.
Thể tích của hộp phấn đó là:
4 × 4 × 4 = 64 (cm3)
Đáp số: 64cm3
Dạng 3: Tính độ dài cạnh khi biết thể tích
Phương pháp: nếu tìm một số a mà a x a x a = V thì độ dài cạnh hình lập phương là a.
Ví dụ. Tính độ dài cạnh của hình lập phương biết rằng thể tích của hình lập phương đó là 512cm3.
Bài giải
Vì 512 = 8 × 8 × 8 nên cạnh của hình lập phương đó là 8cm.
Đáp số: 8cm
Dạng 4: So sánh thể tích của một hình lập phương với thể tích một một hình hộp chữ nhật hoặc với một hình lập phương khác
Phương pháp: Áp dụng công thức để tính thể tích từng hình rồi so sánh.
Ví dụ. Hình hộp chữ nhật có độ dài ba cạnh lần lượt là 6, 7, 8 cm. Một hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật trên. Hỏi hình nào có thể tích lớn hơn và lớn hơn bao nhiêu xăng – ti – mét khối?
Bài giải
Cạnh của hình lập phương là:
(6 + 7 + 8) : 3 = 7 (cm)
Thể tích của hình lập phương là:
7 × 7 × 7 = 343 (cm3)
Thể tích của hình hộp chữ nhật là:
6 × 7 × 8 = 336 (cm3)
Vì 343cm3 > 336cm3 nên hình lập phương có thể tích lớn hơn và lớn hơn số xăng-ti-mét khối là:
343 – 336 = 7 (cm3)
Đáp số: 7cm3
Dạng 5: Toán có lời văn
Phương pháp: Đọc kĩ đề bài, xác định dạng toán và yêu cầu của đề bài rồi giải bài toán đó.
Ví dụ. Một khối kim loại hình lập phương có cạnh là 0,75m. Mỗi đề-xi-mét khối kim loại đó nặng 15kg. Hỏi khối kim loại đó cân nặng bao nhiêu ki-lô-gam?
Bài giải
Đổi: 0,75m = 7,5dm
Thể tích của khối kim loại đó là:
7,5 × 7,5 × 7,5 = 421,875 (dm3)
Khối kim nặng có cân nặng là:
421,875 × 15 = 6328,125 (kg)
Đáp số: 6328,125kg
3. Bài tập vận dụng
Bài 1. Tính thể tích hình lập phương cạnh a:
a) a = 6cm
b) a = 7,5dm
c) a = 4/5m.
Bài 2. Hình lập phương A có cạnh 4cm. Hình lập phương B có cạnh gấp 2 lần cạnh hình lập phương A. Hỏi thể tích hình lập phương B gấp bao nhiêu lần thể tích hình lập phương A?
Bài 3. Một khối kim loại hình lập phương có cnahj 1/5m. Mỗi xăng-ti-mét khối kim loại nặng 6,2g. Hỏi khối kim loại đó cân nặng bao nhiêu ki-lô-gam?
Bài 4. Thể tích của khối lập phương tăng bao nhiêu lần nếu cạnh của khối lập phương đó tăng lên 3 lần?
Bài 5. Một khối gỗ dạng hình lập phương có cạnh 20 cm. Người ta cắt đi một phần gỗ có dạng hình lập phương có cạnh bằng nửa cạnh khối gỗ đó. Tính thể tích phần gỗ còn lại.
Bài 6. Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 96dm2. Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 3,2m2 tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Xem thêm các bài viết về công thức, định nghĩa, tính chất môn Toán hay, chi tiết khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn