Nội dung bài viết
Tổng hợp Công thức Toán lớp 6 (sách mới) | Công thức Toán lớp 6 Số học, Hình học – Tổng hợp Công thức Toán lớp 6 chương trình mới giúp bạn nắm vững kiến thức trọng tâm môn Toán.-Tổng hợp Công thức Toán lớp 6 (sách mới) | Công thức Toán lớp 6 Số học, Hình học
Tổng hợp Công thức Toán lớp 6 (sách mới) | Công thức Toán lớp 6 Số học, Hình học
Việc nhớ chính xác một công thức Toán lớp 6 trong hàng trăm công thức không phải là việc dễ dàng. Bài viết tổng hợp
Công thức Toán lớp 6 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ Học kì 1, Học kì 2 như là cuốn sổ tay công thức giúp bạn học tốt môn Toán 6.
Tổng hợp công thức Toán lớp 6 (sách mới)
Các bài viết Công thức Toán lớp 6 được biên soạn bám sát sách Kết nối tri thức, nếu học sinh lớp 6 học theo sách Chân trời sáng tạo hoặc Cánh diều thì căn cứ và so sánh nội dung để theo dõi bài viết:
Công thức về tính chất của phép cộng số tự nhiên
1. Công thức
a) Cộng hai số tự nhiên
Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.
a + b = c trong đó a, b là 2 số hạng, c là tổng.
b) Tính chất của phép cộng
Phép cộng số tự nhiên có các tính chất:
Với a, b, c là số tự nhiên
– Giao hoán: a + b = b + a
– Kết hợp: (a + b) + c = a + (b + c)
– Cộng với 0: a + 0 = 0 + a = a
2. Ví dụ minh họa:
Ví dụ 1. Tính một cách hợp lí: 117 + 68 + 23.
Hướng dẫn giải:
117 + 68 + 23
= 117 + 23 + 68 (Tính chất giao hoán)
= (117 + 23) + 68 (Tính chất kết hợp)
= 140 + 68 = 208.
Ví dụ 2. Tính một cách hợp lí:
a) 285 + 470 + 115 + 230
b) 571 + 216 + 129 + 124
Hướng dẫn giải:
a) 285 + 470 + 115 + 230
= (285 + 115) + (470 + 230)
= 400 + 700
= 1 100
b) 571 + 216 + 129 + 124
= (571 + 129) + (216 + 124)
= 700 + 340
= 1 040.
Ví dụ 3. Mẹ An mua cho An một bộ đồng phục học sinh gồm: Áo sơ mi giá 125 000 đồng, áo khoác giá 140 000 đồng, quần âu giá 160 000 đồng. Tính số tiền mẹ An đã mua đồng phục cho An.
Hướng dẫn giải:
Số tiền mẹ An đã mua đồng phục cho An là:
125 000 + 140 000 + 160 000 = 425 000 (đồng)
Vậy số tiền mẹ An đã mua đồng phục là 425 000 đồng
3. Bài tập tự luyện
Bài 1. Thay “?” bằng số thích hợp:
? + 2 895 = 2 895 + 6 789
Bài 2. Tính
a ) 5264 + 3978 + 4736.
b ) 42716 + 37284 + 6767.
Bài 3. Tính bằng cách thuận tiện nhất :
a ) 81 + 35 + 19.
b ) 78 + 65 + 135 + 22.
Bài 4. Một xã tổ chức tiêm phòng bệnh cho trẻ em. Lần đầu có 1465 em tiêm phòng bệnh, lần sau có nhiều hơn lần đầu 335 em tiêm phòng bệnh. Hỏi cả hai lần có bao nhiêu em đã tiêm phòng bệnh?
Bài 5. Tính nhanh:
a) 145 + 86 + 14 + 55.
b) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.
c) 34000 + 57859 + 66000.
d) 8973 + 45783 + 46027 + 54217.
…………………………..
…………………………..
…………………………..
Công thức về tính chất của phép nhân số tự nhiên
1. Công thức
a) Nhân hai số tự nhiên
Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên gọi là tích của chúng, kí hiệu là a × b hoặc a . b:
a . b = a + a + … + a (b số hạng).
a . b = c trong đó a, b là 2 thừa số, c là tích.
Nếu các thừa số đều bằng chữ hoặc chỉ có một thừa số là số thì ta có thể không viết dấu nhân giữa các thừa số, chẳng hạn a . b = ab; 2 . m = 2m.
b) Tính chất của phép nhân
Phép nhân số tự nhiên có các tính chất:
Với a, b, c là số tự nhiên
– Giao hoán: ab = ba
– Kết hợp: (ab)c = a(bc)
– Phân phối của phép nhân đối với phép cộng: a(b + c) = ab + ac.
– Nhân với số 1: a . 1 = 1 . a = a.
– Nhân với số 0: a . 0 = 0.
2. Ví dụ minh họa:
Ví dụ 1. Tìm số tự nhiên c sao cho (3 . 2) . 5 = 3 . (2 . c).
Hướng dẫn giải:
Ta có:
(3 . 2) . 5
= 3 . (2 . 5) (Tính chất kết hợp)
= 3 . (2 . c)
Do đó c = 5
Ví dụ 2. Tính nhanh:
a) 4 . 37 . 25;
b) 87 . 36 + 87 . 64
Hướng dẫn giải:
a) 4 . 37 . 25
= 4 . 25 . 37 (Tính chất giao hoán)
= (4 . 25) . 37
= 100 . 37 = 3700
b) 87 . 36 + 87 . 64
= 87 . (36 + 64) (Tính chất phân phối của phép nhân đối với phép cộng)
= 87 . 100 = 8700
Ví dụ 3.Không đặt tính, hãy so sánh:
a) m = 19. 90 và n = 31. 60
b) p = 2 011. 2 019 và q = 2 015. 2 015.
Hướng dẫn giải:
a)
m = 19 . 90 = 19 . (3 . 30) = (19 . 3) . 30
n = 31 . 60 = 31. (3 . 20) = (20 . 3) . 31
Vì 19 < 20; 30 < 31 nên (19 . 3) . 30 < (20 . 3) . 31 hay m < n.
Vậy m < n.
b)
p = 2 011 . 2 019 = 2 011 . (2 015 + 4) = 2 011 . 2 015 + 2 011 . 4
q = 2 015 . 2 015 = (2 011 + 4) . 2 015 = 2 011 . 2 015 + 4 . 2015
= 2 011 . 2 015 + 2 015 . 4
Vì 2 011 < 2 015 nên 2 011 . 4 < 2 015 . 4
hay 2 011 . 2 015 + 2 011 . 4 < 2 011 . 2 015 + 2 015 . 4
Do đó p < q.
3. Bài tập tự luyện
Bài 1. Một trường học lên kế hoạch thay tất cả các bóng đèn sợi đốt bình thường bằng bóng đèn led cho 20 phòng học, mỗi phòng 8 bóng. Nếu mỗi bóng đèn led có giá 94 000 đồng thì nhà trường phải trả bao nhiêu tiền để thay đủ đèn led cho tất cả các phòng học?
Bài 2. Một xe ô tô chở 50 bao gạo và 70 bao ngô. Biết rằng mỗi bao gạo nặng 45kg, mỗi bao ngô nặng 55kg. Hỏi xe ô tô chở tất cả bao nhiêu kilôgam gạo và ngô?
Bài 3. Tính nhẩm:
a ) 125 . 101
b ) 21 . 49
c) 121 . 25 . 4
d) 3025 . 125 . 8
Bài 4. Tính:
a) 26 + 26 . 137
b) 63 . 25 + 25 . 23
c) 96 . (15 + 24) + 96 . (26 + 35)
d) 25 . 26 . 4
Bài 5. Tính nhanh:
a) 4 . 125 . 25 . 6 . 8
b) 98 . (1 + 96) + 3 . 98
…………………………..
…………………………..
…………………………..
Lưu trữ: Công thức Toán lớp 6 (sách cũ)
1. Tập hợp. Phần tử của tập hợp:
– Tập hợp là một khái niệm cơ bản. Ta hiểu tập hợp thông qua các ví dụ.
– Tên tập hợp được đặt bằng chữ cái in hoa.
– Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “;” (nếu có phần tử là số) hoặc dấu “,”. Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
– Kí hiệu: 1 ∈ A đọc là 1 thuộc A hoặc 1 là phần tử của A;
5 ∉ A đọc là 5 không thuộc A hoặc 5 không là phần tử của A;
– Để viết một tập hợp, thường có hai cách:
+ Liệt kê các phần tử của tập hợp.
+ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
– Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào (tức tập hợp rỗng, kí hiệu ∅ ).
– Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A ⊂ B đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.
– Mỗi tập hợp đều là tập hợp con của chính nó. Quy ước: tập hợp rỗng là tập hợp con của mọi tập hợp.
* Cách tìm số tập hợp con của một tập hợp: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2n.
– Giao của hai tập hợp (kí hiệu: ∩) là một tập hợp gồm các phần tử chung của hai tập hợp đó.
2. Tập hợp các số tự nhiên: Kí hiệu N
– Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Điểm biểu diễn số tự nhiên a trên tia số gọi là điểm a.
– Tập hợp các số tự nhiên khác 0 được kí hiệu là N*.
– Thứ tự trong tập hợp số tự nhiên:
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia. Trên hai điểm trên tia số, điểm ở bên trái biểu diễn số nhỏ hơn.
+ Nếu a < b và b < c thì a < c.
+ Mỗi số tự nhiên có một số liền sau duy nhất, chẳng hạn số tự nhiên liền sau số 2 là số 3; số liền trước số 3 là số 2; số 2 và số 3 là hai số tự nhiên liên tiếp. Hai số tự nhiên liên tiếp thì hơn kém nhau một đơn vị.
+ Số 0 là số tự nhiên nhỏ nhất. Không có số tự nhiên lớn nhất.
+ Tập hợp các số tự nhiên có vô số phần tử.
3. Ghi số tự nhiên: Có nhiều cách ghi số khác nhau:
– Cách ghi số trong hệ thập phân: Để ghi các số tự nhiên ta dùng 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Cứ 10 đơn vị ở một hàng thì làm thành một đơn vị ở hàng liền trước nó.
+ Kí hiệu: 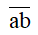 chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a, chữ số hàng đơn vị là b. Viết được
chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a, chữ số hàng đơn vị là b. Viết được 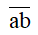 = a.10 + b
= a.10 + b
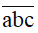 chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a, chữ số hàng chục là b, chữ số hàng đơn vị là c. Viết được
chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a, chữ số hàng chục là b, chữ số hàng đơn vị là c. Viết được 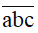 = a.100 + b.10 + c
= a.100 + b.10 + c
– Cách ghi số La Mã: có 7 chữ số
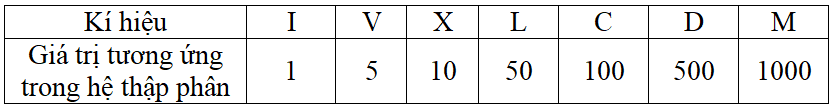
+ Mỗi chữ số La Mã không viết liền nhau quá ba lần.
+ Chữ số có giá trị nhỏ đứng trước chữ số có giá trị lớn làm giảm giá trị của chữ số có giá trị lớn.
– Cách ghi số trong hệ nhị phân: để ghi các số tự nhiên ta dùng 2 chữ số là : 0 và 1.
– Các ví dụ tách một số thành một tổng:
Trong hệ thập phân: 6478 = 6. 103 + 4. 102 + 7. 101 + 8. 100
Trong hệ nhị phân: 1101 = 1. 23 + 1. 22 + 0. 21 + 1. 20
4. Các phép toán:
a, Phép cộng:
a + b = c
(số hạng) + (số hạng) = (tổng)
b, Phép trừ: Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao cho b + x = a thì ta có phép trừ
a – b = x
(số bị trừ) – (số trừ) = (hiệu)
c, Phép nhân:
a . b = d
(thừa số) . (thừa số) = (tích)
d, Phép chia: Cho hai số tự nhiên a và b, trong đó b ≠ 0, nếu có số tự nhiên x sao cho b.x = a thì ta nói a chia hết cho b và ta có phép chia hết
a : b = x
(số bị chia) : (số chia) = (thương)
Tổng quát: Cho hai số tự nhiên a và b, trong đó b ≠ 0, ta luôn tìm được hai số tự nhiên q và r duy nhất sao cho:
a = b . q + r trong đó 0 ≤ r < b
(số bị chia) = (số chia) . (thương) + (số dư)
Nếu r = 0 thì ta có phép chia hết.
Nếu r ≠ 0 thì ta có phép chia có dư.
* Tính chất của phép cộng và phép nhân số tự nhiên:
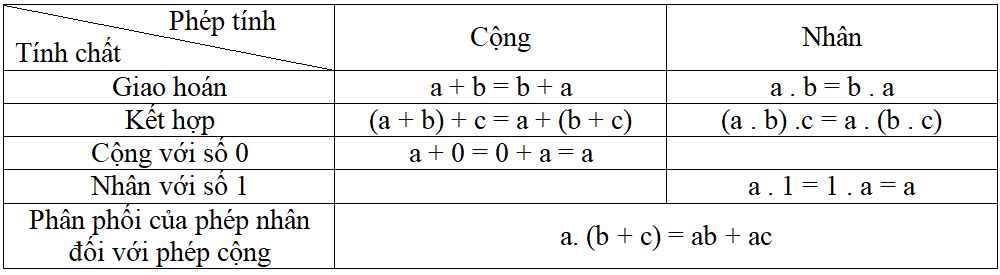
e, Chú ý:
+ Trong tính toán có thể thực hiện tương tự với tính chất a(b – c) = ab – ac
+ Dạng tổng quát của số chẵn (số chia hết cho 2) là 2k (k ∈ N), dạng tổng quát của số lẻ (số chia cho 2 dư 1) là 2k + 1 (k ∈ N).
f, Phép nâng lên lũy thừa:
– ĐN: Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.
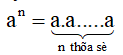 (n ≠ 0); a gọi là cơ số, n gọi là số mũ.
(n ≠ 0); a gọi là cơ số, n gọi là số mũ.
a2 gọi là a bình phương (hay bình phương của a);
a3 gọi là a lập phương (hay lập phương của a)
Quy ước: a1 = a ; a0 = 1 (a ≠ 0)
– Nhân hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
am . an = am + n
– Chia hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.
am : an = am – n (với a ≠ 0; m ≥ n )
– Thêm: (am)n = am.n ; (a.b)n = an. bn
* Số chính phương: là số bằng bình phương của một số tự nhiên (VD: 0, 1, 4, 9, …)
5. Thứ tự thực hiện các phép tính:
– Đối với biểu thức không có dấu ngoặc:
+ Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện theo thứ tự: Lũy thừa → Nhân và chia → Cộng và trừ.
– Đối với biểu thức có dấu ngoặc ta thực hiện theo thứ tự ( ) → [ ] → { }
6. Tính chất chia hết của một tổng:
– Tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
a  m, b
m, b 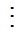 m, c
m, c 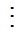 m ⇒ (a + b + c)
m ⇒ (a + b + c) 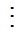 m
m
– Tính chất 2: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
a 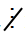 m, b
m, b 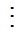 m, c
m, c 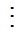 m ⇒ (a + b + c)
m ⇒ (a + b + c) 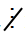 m
m
7. Dấu hiệu chia hết cho 2, 3, 5, 9:

8. Ước và bội:
– Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.
– Ta có thể tìm các bội của một số bằng cách nhân số đó lần lượt với 0, 1, 2, 3,…
– Ta có thể tìm các ước của a bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a
– Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó. Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.
* Cách kiểm tra 1 số là số nguyên tố: Để kết luận số a là số nguyên tố (a > 1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.
– Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố
* Cách tính số lượng các ước của một số m (m > 1): ta xét dạng phân tích của số m ra thừa số nguyên tố: Nếu m = ax thì m có x + 1 ước
Nếu m = ax. by thì m có (x + 1)(y + 1) ước
Nếu m = ax. by. cz thì m có (x + 1)(y + 1)(z + 1) ước.
– Ước chung của hai hay nhiều số là ước của tất cả các số đó.
– Bội chung của hai hay nhiều số là bội của tất cả các số đó.
– ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
– Các số nguyên tố cùng nhau là các số có ƯCLN bằng 1
– Để tìm ước chung của các số đã cho, ta có thể tìm các ước của ƯCLN của các số đó.
– BCNN của hai hay nhiều số là số lớn nhất khác 0 trong tập hợp các bội chung của các số đó.
– Để tìm BC của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.
– Cách tìm ƯCLN và BCNN:

* Bổ sung:
+ Tích của hai số tự nhiên khác 0 bằng tích của ƯCLN và BCNN của chúng:
a . b = ƯCLN(a,b). BCNN(a,b)
+ Nếu tích a.b chia hết cho m, trong đó b và m là hai số nguyên tố cùng nhau thì a m
+ Một cách khác tìm ƯCLN của hai số a và b (với a > b):
Chia số lớn cho số nhỏ.
Nếu a 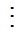 b thì ƯCLN(a,b) = b
b thì ƯCLN(a,b) = b
– Nếu phép chia a cho b có số dư r1, lấy b chia cho r1.
– Nếu phép chia b cho r1 có số dư r2, lấy r1 chia cho r2.
– Cứ tiếp tục như vậy cho đến khi số dư bằng 0 thì số chia cuối cùng là ƯCLN phải tìm.
1. Dấu chấm nhỏ trên trang giấy là hình ảnh của điểm (Dùng các chữ cái in hoa: A, B, C, …để đặt tên cho điểm).
2. Bất cứ hình nào cũng là tập hợp tất cả những điểm. Một điểm cũng là một hình.
3. Sợi chỉ căng thẳng, mép bảng,… cho ta hình ảnh của đường thẳng. Đường thẳng không bị giới hạn về hai phía.
4. Khi ba điểm A, B, C cùng thuộc một đường thẳng, ta nói chúng thẳng hàng
5. Khi ba điểm A, B, C không cùng thuộc bất kì đường thẳng nào, ta nói chúng không thẳng hàng.
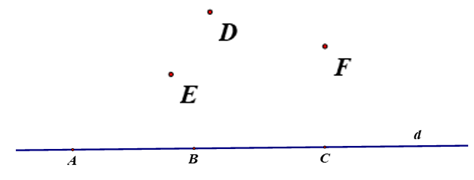
Kí hiệu: điểm A thuộc đường thẳng d; điểm D không thuộc đường thẳng D
6. Nhận xét: Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
7. Nhận xét: Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm A và B.
8. Có ba cách gọi tên một đường thẳng: một chữ cái thường, hai chữ cái thường, đường thẳng đi qua hai chữ cái in hoa (đường thẳng AB,…)
9. Ba vị trí tương đối giữa hai đường thẳng:
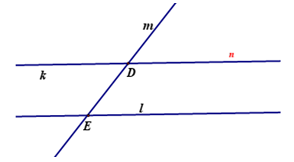
– Trùng nhau (k ≡ n)
– Cắt nhau (m ∩ l ; m ∩ k)
– Song song (k // l)
Hai đường thẳng không trùng nhau còn được gọi là hai đường thẳng phân biệt. Hai đường thẳng phân biệt hoặc chỉ có một điểm chung hoặc không có điểm chung nào.
10. Tia: Hình gồm điểm O và một phần đường thẳng bị chia ra bởi O được gọi là một tia gốc O (còn được gọi là một nửa đường thẳng gốc O)

+) Hai tia chung gốc Ox và Oy tạo thành đường thẳng xy được gọi là hai tia đối nhau.

Nhận xét: Mỗi điểm trên đường thẳng là gốc chung của hai tia đối nhau.
+) Hai tia trùng nhau: Tia Ox và tia OB trùng nhau

11. Đoạn thẳng AB là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B. Hai điểm A, B là hai mút (hoặc hai đầu)
12. Nhận xét: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB. Ngược lại, nếu AM + MB = AB thì điểm M nằm giữa hai điểm A và B.

13. Trên tia Ox bao giờ cũng vẽ được một và chỉ một điểm M sao cho OM= a (đvđd)
14. Trên tia Ox, OM = a, ON = b, nếu 0 < a < b thì điểm M nằm giữa hai điểm O và N.

15. Trung điểm M của đoạn thẳng AB là điểm nằm giữa A, B và cách đều A, B (MA = MB). Trung điểm của đoạn thẳng AB còn được gọi là điểm chính giữa của đoạn thẳng AB.

M là trung điểm của AB ⇔ 
Hoặc M là trung điểm của AB ⇔ 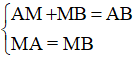
Hoặc M là trung điểm của AB ⇔ 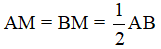
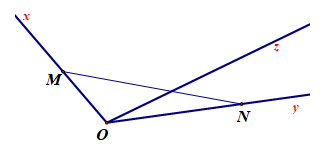
16. Tia nằm giữa hai tia: Cho 3 tia Ox, Oy, Oz chung gốc. Lấy điểm M bất kì trên tia Ox, lấy điểm N bất kì trên tia Oy (M và N đều không trùng với điểm O). Nếu tia Oz cắt đoạn thẳng MN tại một điểm nằm giữa M và N ta nói tia Oz nằm giữa hai tia Ox, Oy.
Các bài học để học tốt các môn học lớp 6 Kết nối tri thức hay khác:
Các bài học để học tốt các môn học lớp 6 Chân trời sáng tạo hay khác:
Các bài học để học tốt các môn học lớp 6 Cánh diều hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn