Lý thuyết Đa thức một biến lớp 7 (hay, chi tiết) – Tổng hợp lý thuyết Toán lớp 7 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 7.-Lý thuyết Đa thức một biến lớp 7 (hay, chi tiết)
Lý thuyết Đa thức một biến lớp 7 (hay, chi tiết)
Bài viết Lý thuyết Đa thức một biến lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Đa thức một biến.
Lý thuyết Đa thức một biến lớp 7 (hay, chi tiết)
1. Đa thức một biến
• Đa thức một biến là tổng của những đơn thức của cùng một biến.
• Một số được coi là một đa thức một biến.
• Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.
Ví dụ 1: Đa thức 5x5 + 4x3 – 2x2 + x là đa thức một biến (biến x); bậc của đa thức là 5.
Ví dụ 2: Cho đa thức sau: 5x7 – 7x6 + 5x5 – 4x4 + 7x6 – 3x2 + 1 – 5x7 – 3x5
Bậc của đa thức đã cho là bao nhiêu?
Hướng dẫn giải:
Thu gọn đa thức ta được:
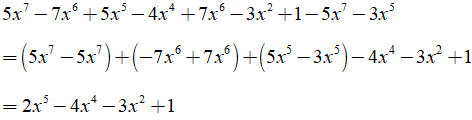
Đa thức đã cho có bậc là 5.
2. Sắp xếp một đa thức một biến
Để thuận lợi cho việc tính toán đối với các đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến.
Ví dụ 1: Đối với đa thức P(x) = 6x + 3 – 6x2 + x3 + 2x4
+ Khi sắp xếp các hạng tử của nó theo lũy thừa giảm của biến, ta được:
P(x) = 2x4 + x3 – 6x2 + 6x + 3
+ Khi sắp xếp các hạng tử của nó theo lũy thừa tăng của biến, ta được:
P(x) = 3 + 6x – 6x2 + x3 + 2x4
Nhận xét:
Mọi đa thức bậc 2 của biến x, sau khi đã sắp xếp các hạng tử của chúng theo lũy thừa giảm của biến, đều có dạng: ax2 + bx + c
Trong đó a,b,c là các số cho trước và a ≠ 0.
Chú ý:
+ Để sắp xếp các hạng tử của một đa thức, trước hết ta phải thu gọn đa thức đó.
+ Những chữ đại diện cho các số xác định cho trước được gọi là hằng số.
Ví dụ 2: Cho đa thức P(x) = 2 + 5x2 – 3x3 + 4x – 2x – x3 + 6x5. Thu gọn và sắp xếp đa thức
P(x) = 2 + 5x2 – 3x3 + 4x2 – 2x – x3 + 6x5 = 6x5 + (-3x3 – x3) + (5x2 + 4x2) – 2x + 2 = 6x5 – 4x3 + 9x2 – 2x + 2
3. Hệ số
Hệ số của lũy thừa bậc 0 của biến gọi là hệ số tự do; hệ số của lũy thừa cao nhất của biến gọi là hệ số cao nhất.
Ví dụ: Các hệ số của đa thức 6x5 – x4 + 5x2 – x + 2 là 6; -1; 5; -1; 2
Hệ số tự do là: 2
Hệ số cao nhất là: 6
Bài 1: Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm dần của biến
a) 2x3 – x5 + 3x4 + x2 – (1/2)x3 + 3x5 – 2x2 – x4 + 1
b) x7 – 3x4 + 2x3 – x2 – x4 – x + x7 – x3 + 5
Lời giải:
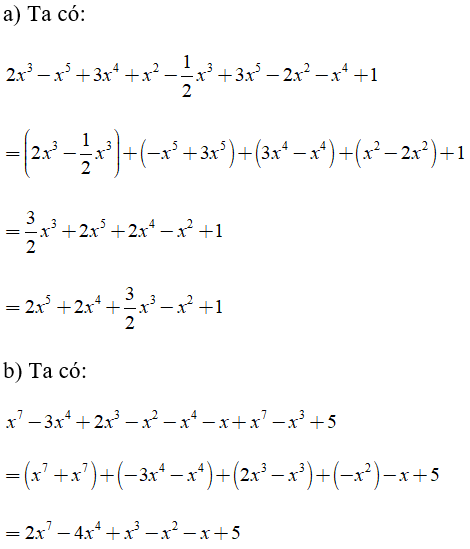
Bài 2: Tính giá trị của các biểu thức sau:
a) x + x2 + x3 + x4 + …. + x99 + x100 tại x = -1
b) x2 + x4 + x6 + …. + x98 + x100 tại x = -1
Lời giải:
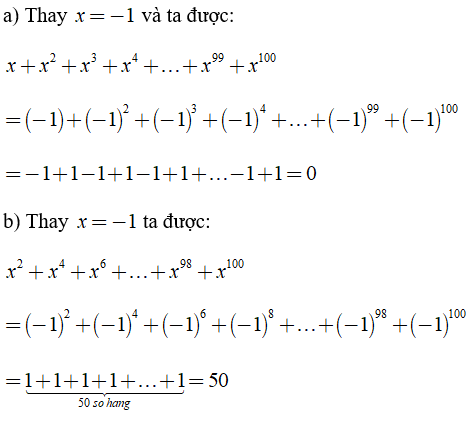
Bài 1. Thu gọn đa thức sau:
Q = 5x2y−3xy+12x2y−xy+5xy−13x+12+23x−14.
Hướng dẫn giải:
Q = 5x2y−3xy+12x2y−xy+5xy−13x+12+23x−14
= 5x2y+12x2y+−3xy−xy+5xy+−13x+23x+12−14
= 5+12x2y+−3−1+5xy+−13+23x+14
= 112x2y+xy+13x+14
Bài 2. Thu gọn đa thức sau:
A = x2 + y2 + z2 + x2 – y2 + z2 + x2 + y2 – z2.
Hướng dẫn giải:
Q = x2 + y2 + z2 + x2 – y2 + z2 + x2 + y2 – z2
= (x2 + x2 + x2) + (y2 – y2 + y2) + (z2 – z2 + z2)
= 3x2 + y2 + z2.
Bài 3. Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
P = 13x2y+xy2−xy+12xy2−5xy−13x2y
Hướng dẫn giải:
Ta có
P = 13x2y+xy2−xy+12xy2−5xy−13x2y
= 0+1+12xy2+−1−5xy=32xy2−6xy
Thay x = 0,5 = 12 và y = 1 vào P ta được:
P = 32.12.12−6.12.1=34−3=−94
Vậy P = −94 khi x = 0,5 và y = 1.
Bài 4. Cho A(x) = 3×4−34×3+2×2−3; B(x) = 8×4+15×3−9x+25.
Tính A(x) + B(x).
Hướng dẫn giải:
A(x) + B(x) = 3×4−34×3+2×2−3+8×4+15×3−9x+25
= (3×4+8×4)+−34×3+15×3+2×2−9x+−3+25
= 11×4−1120×3+2×2−9x−135
Bài 5. Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm dần của biến:
a) 2x4 – 2x5 + x4 + x – x3 + 2x5 – 5x2 – x4 + 1;
b) x2 – 2x3 + 2x2 – x7 – x4 – x + 2x7 – 3x3 + 5.
Hướng dẫn giải:
a) 2x4 – 2x5 + x4 + x – x3 + 2x5 – 5x2 – x4 + 1
= (2x4 + x4 – x4) + (–2x5 + 2x5) + x − x3 – 5x2 + 1
= 2x4 + x – x3 – 5x2 + 1
= 2x4 – x3 – 5x2 + x + 1
b) x2 – 2x3 + 2x2 – x7 – x4 – x + 2x7 – 3x3 + 5
= (x2 + 2x2) + (−2x3 – 3x3) + (−x7 + 2x7) – x4 – x + 5
= 3x2 – 5x3 + x7 – x4 – x + 5
= x7 – x4 – 5x3 + 3x2 – x + 5
Bài 6. Cho đa thức A(x) = x2 – 4x – 5. Trong các số – 1; 0 và 1, số nào là nghiệm của đa thức A(x)?
Bài 7. Cho hai đa thức:
P(x) = – 2x4 – 7x + 12 – 6x4 + 2x2 – x;
Q(x) = 3x3 – x4 – 5x2 + x3 – 6x + 9 + x4.
a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.
b) Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức trên.
Bài 8. Tính rồi tìm hệ số và bậc của đơn thức nhận được.
a) −12x.8×3;
b) 12×2−32×2;
c) 18×5.2×3;
d) −9×4+2×22.
Bài 9. Tìm giá trị của đa thức 2x2 – 3x + 1 khi x = 4.
Bài 10. Tính tổng và hiệu của các đa thức sau:
a) 3x2 + 2x – 7 và 5x2 – x + 4;
b) 4x3 + 2x2 – 5x + 1 và 2x3 – 3x2 + 6x – 2.
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:
Lời giải bài tập lớp 7 sách mới:

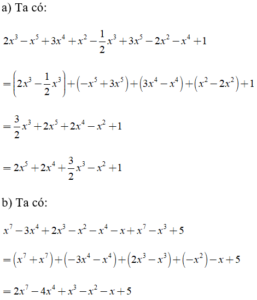
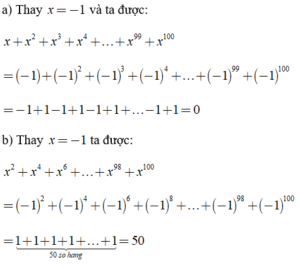

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn