Lý thuyết Đường trung bình của tam giác, của hình thang lớp 8 (hay, chi tiết) – Tổng hợp Lý thuyết Toán 8 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 8.-Lý thuyết Đường trung bình của tam giác, của hình thang lớp 8 (hay, chi tiết)
Lý thuyết Đường trung bình của tam giác, của hình thang lớp 8 (hay, chi tiết)
Bài viết Lý thuyết Đường trung bình của tam giác, của hình thang lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Đường trung bình của tam giác, của hình thang.
Lý thuyết Đường trung bình của tam giác, của hình thang lớp 8 (hay, chi tiết)
Bài giảng: Bài 4: Đường trung bình của tam giác, của hình thang – Cô Phạm Thị Huệ Chi (Giáo viên Meraki Center)
1. Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lý:
Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba,
Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Δ ABC,AD = DB,AE = EC ⇒ DE//BC,DE = 1/2BC.
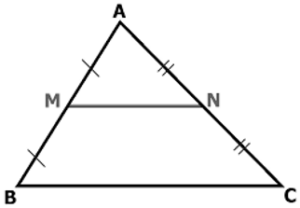
Ví dụ: Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4( cm ). Tính độ dài MN.
Lời giải:
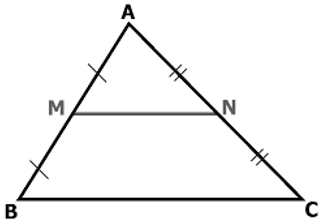
Theo giả thiết ta có M là trung điểm của AB, N là trung điểm của AC
⇒ MN là đường trung bình của Δ ABC.
Áp dụng định lý 2, ta có MN = 1/2BC.
⇒ MN = 1/2BC = 1/2.4 = 2( cm )
2. Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lý:
Định lí 1: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 2: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
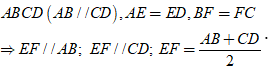
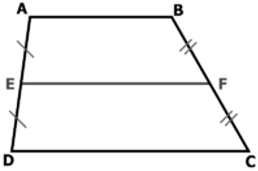
Ví dụ: Cho hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC và AB = 4( cm ) và CD = 7( cm ). Tính độ dài đoạn EF.
Lời giải:
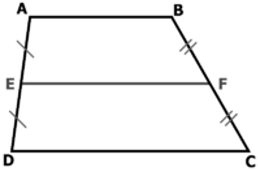
Ta có hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC
⇒ EF là đường trung bình của hình thang.
Áp dụng định lý 2, ta có EF = (AB + CD)/2
⇒ EF = (AB + CD)/2 = (4 + 7)/2 = 5,5( cm ).
Bài 1: Cho tam giác ABC( AB > AC ) có Aˆ = 500. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD,BC. Tính BEFˆ = ?
Lời giải:
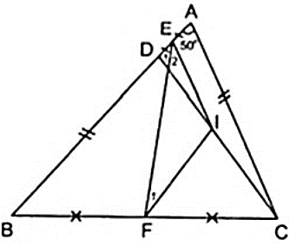
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác ACD và BCD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC
Từ ( 1 ) ⇒ E1ˆ = F1ˆ (vì so le trong) ( 5 )
Từ ( 2 ) và ( 3 ) ⇒ FI = EI nên E2ˆ = F1ˆ (vì trong tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau) ( 6 )
Từ ( 5 ) và ( 6 ) ⇒ E1ˆ = E2ˆ
Từ ( 4 ) ⇒ BEIˆ = Aˆ = 500 (vì đồng vị)
Mà BEIˆ = 2E1ˆ ⇒ E1ˆ = 250
Bài 2: Cho hình thang ABCD ( AB//CD ) có AB = 2cm,CD = 5cm,AD = 7cm. Gọi E là trung điểm của BC. Tính AEDˆ = ?
Lời giải:
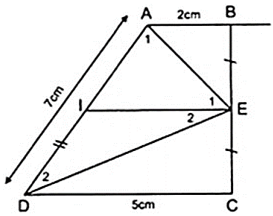
Đặt E1ˆ = α ,E2ˆ = β ⇒ AEDˆ = α + β
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì AI = ID = AD/2 = 3,5( cm ). ( 1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có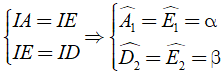
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có A1ˆ + AEDˆ + D2ˆ = 1800
Hay α + α + β + β = 2( α + β ) = 1800 ⇒ α + β = 900
Do α + β = 900 nên AEDˆ = 900.
Bài giảng: Bài 4: Đường trung bình của tam giác, của hình thang (Phần 2) – Cô Phạm Thị Huệ Chi (Giáo viên Meraki Center)
Bài giảng: Bài 4: Đường trung bình của tam giác, của hình thang – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

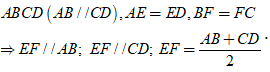

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn