Một số hệ thức về cạnh và đường cao trong tam giác vuông | Chuyên đề Toán 9 – Tuyển tập chuyên đề Toán 9 chọn lọc với đầy đủ phương pháp giải, bài tập tự luận, trắc nghiệm giúp bạn học tốt môn Toán 9.-Một số hệ thức về cạnh và đường cao trong tam giác vuông
Một số hệ thức về cạnh và đường cao trong tam giác vuông
Cách giải Một số hệ thức về cạnh và đường cao trong tam giác vuông lớp 9 với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh
ôn tập, biết cách làm bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông.
Một số hệ thức về cạnh và đường cao trong tam giác vuông
A. Phương pháp giải
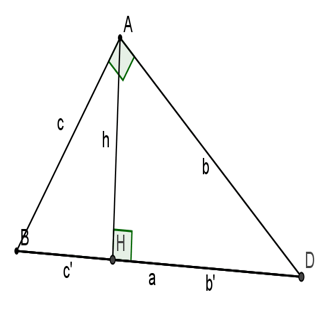
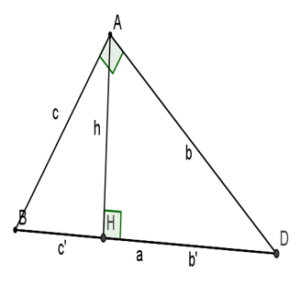
Cho tam giác ABC vuông góc tại A, đường cao AH. Khi đó ta có:
1, c2 = ac’, b2 = ab’
2, a2 = b2 + c2
3, ah = bc
4, h2 = b’.c’
5, 1/h2 = 1/b2 + 1/c2
B. Bài tập tự luận
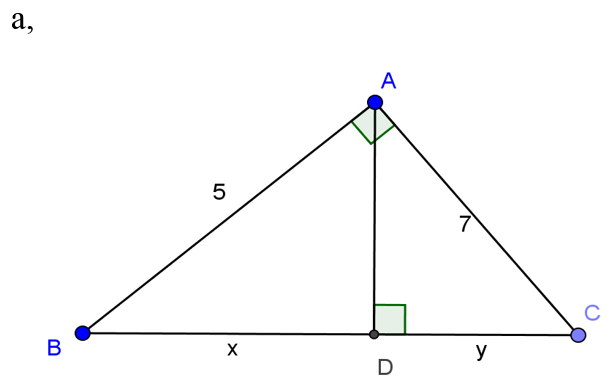
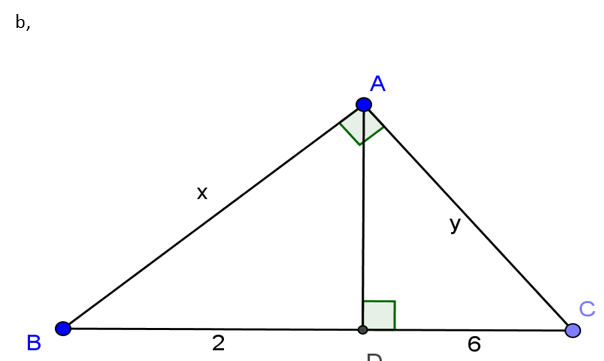
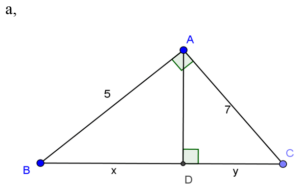
Bài 1: Tính x, y trong các trường hợp sau
Hướng dẫn giải
a, Áp dụng định lý py-ta-go vào tam giác vuông ABC có:
BC2= AB2+ AC2
BC2= 52+ 72
BC2= 74
Suy ra BC = √74
Áp dụng hệ thức lượng vào tam giac vuông ABC: AB2 = BD.BC
=> BD = AB2/BC => x = 25/√74
DC = BC – BD = √74 – 25/√74 = 49/√74
Vậy x = 25/√74 và y = 49/√74
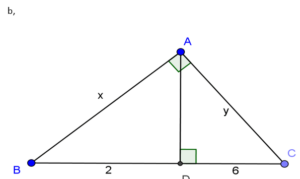
b) Ta có: BC= BD + DC = 2 + 6 = 8
Áp dụng hệ thức lượng ta có:
AB2= BD.BC = 2.8 = 16. Suy ra AB = 4 hay x = 4.
AC2= DC.BC = 6.8 = 48. Suy ra AC = √48 hay y = √48
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
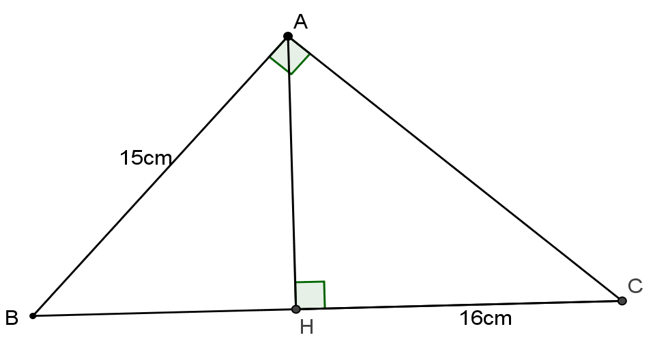
Hướng dẫn giải
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AC2 = CH.BC = 16.BC
AB2 + AC2 = BC2
⇔ 152 + 16.BC = BC2
⇔ BC2 – 16.BC – 225 = 0
⇔ BC2 – 25BC + 9BC – 225 = 0
⇔ BC(BC – 25) + 9(BC – 25) = 0
⇔ (BC – 25)(BC + 9) = 0
⇔ BC = 25 hoặc BC = -9(loại)
=> AC2 = 16.BC = 16.25 = 400
=> AC = 20
+ Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)
Vậy BC=25(cm); AC=20(cm); AH=12(cm)
Bài 3: Cho tam giác ABC có AB = 48cm, BC = 50cm, AC = 14cm. Tính độ dài phân giác giác góc C
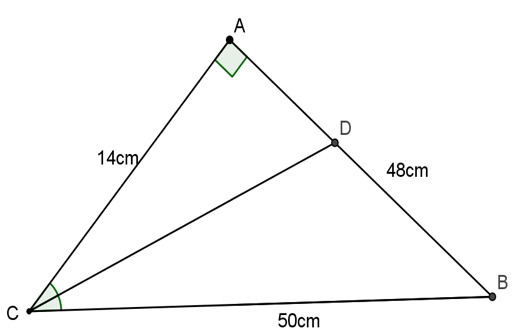
Hướng dẫn giải
Xét tam giác ABC, ta có
BC2 = 502 = 2500
AB2 + AC2 = 142 + 482 = 2500
=> BC2 = AB2 + AC2
=> Tam giác ABC vuông tại A
Có DA/DB = CA/CB = 14/50 = 7/25 (tính chất tia phân giác)
=> DB = 25/7 DA.
Ta có DA + DB = AB
⇔ DA + 25/7 DA = AB ⇔ DA. 32/7 = 48 ⇔ DA = 10,5cm
Xét tam giác vuông ACD, theo đinh lí Pi-ta-go ta có
CD2 = AC2 + AD2 = 142 + 10,52 = 306,25 => CD = 17,5cm
Bài 4: Cho tam giác ABC vuông tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
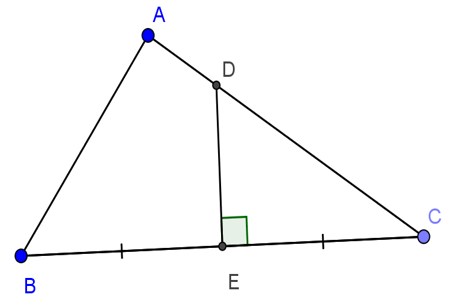
Hướng dẫn giải
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có ∠A = ∠E = 90o
∠C chung
=> Tam giác ACB ∾ tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
C. Bài tập tự luyện
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH.
a) Cho biết AH = 6 cm, BH = 4,5 cm. Tính độ dài các đoạn thẳng AB, AC, BC, HC.
b) Cho biết AB = 6 cm, BH = 3 cm. Tính độ dài các đoạn thẳng AH, AC, CH.
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết AH = 12 cm và BH = 34AH.
Bài 3. Cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền.
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH. Biết ABAC=57 và AH = 15 cm. Tính độ dài đoạn thẳng HB và HC.
Bài 5. Cho ABCD là hình thang vuông tại A và D. Đường chéo BD ⊥ BC. Biết AD = 12 cm và DC = 25 cm. Tính độ dài AB, BC và BD.
Tham khảo thêm các Chuyên đề Toán lớp 9 khác:
Mục lục các Chuyên đề Toán lớp 9:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn