Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C) – Chuyên đề Toán 8 tổng hợp phương pháp giải các dạng bài tập Toán 8 hay, chi tiết giúp bạn học tốt Toán lớp 8.-Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C)
Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C)
Với Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C) môn Toán lớp 8 phần Hình học sẽ giúp học sinh ôn tập, củng cố kiến thức từ đó biết cách làm các dạng bài tập Toán lớp 8 Chương 3: Tam giác đồng dạng để đạt điểm cao trong các bài thi môn Toán 8.
Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C)
Dạng bài: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai
(c – g – c)
A. Phương pháp giải
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
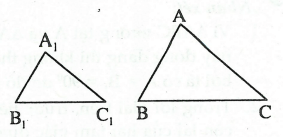 Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
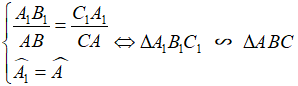
Và khi đó, ta có ngay :
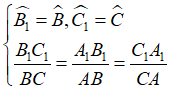
+) Xét hai tam giác, chọn ra hai góc bằng nhau, xét tỉ số hai cạnh tạo nên mỗi góc đó. Nếu hai tỉ số bằng nhau thì hai tam giác đồng dạng.
B. Ví dụ minh họa
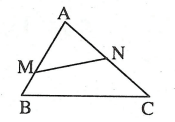 Câu 1: Cho ΔABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB lấy điểm M sao cho AM = 10cm. Trên cạnh AC lấy điểm N sao cho AN = 8cm.
Câu 1: Cho ΔABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB lấy điểm M sao cho AM = 10cm. Trên cạnh AC lấy điểm N sao cho AN = 8cm.
a) Tam giác ΔAMN đồng dạng với tam giác nào?
b) Tính độ dài đoạn MN.
Lời giải:
a. Với hai tam giác ΔAMN và ΔABC, ta có :
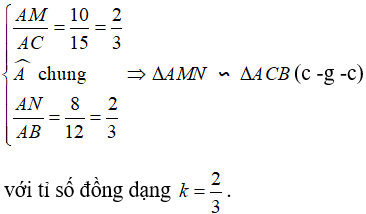
b. Theo câu a), vì ΔAMN và ΔABC
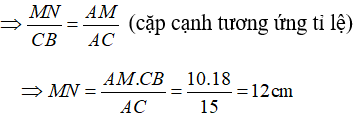
Vậy MN = 12cm.
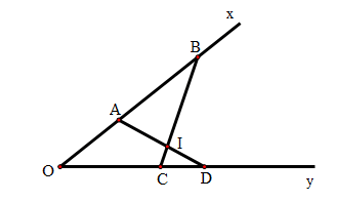
Câu 2: Cho góc 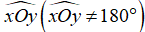 . Trên Ox lấy hai điểm A,B sao cho OA = 3cm, OB = 8cm. Trên Oy lấy hai điểm C,D sao cho OC = 4cm, OD = 6cm.
. Trên Ox lấy hai điểm A,B sao cho OA = 3cm, OB = 8cm. Trên Oy lấy hai điểm C,D sao cho OC = 4cm, OD = 6cm.
a. Chứng minh rằng hai tam giác ΔOAD và ΔOCB đồng dạng.
b. Gọi I là giao điểm của AD và BC. Chứng minh rằng hai tam giác ΔIAB và ΔICD có các góc bằng nhau từng đôi một.
Lời giải:
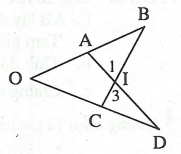 a. Với hai tam giác ΔOAD và ΔOCB, ta có :
a. Với hai tam giác ΔOAD và ΔOCB, ta có :
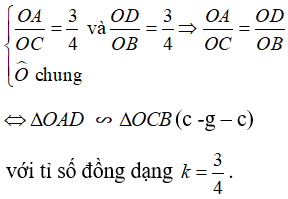
b. Vì ΔOAD và ΔOCB(cmt) 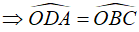 (hai góc tương ứng)
(hai góc tương ứng)
Với hai tam giác ΔIAB và ΔICD, ta có :
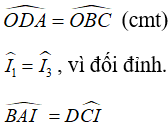
(dựa trên tính chất tổng ba góc trong tam giác bằng 1800).
Vậy, hai tam giác ΔIAB và ΔICD có các góc bằng nhau từng đôi một.
Câu 3: Cho ΔABC có AB = 4cm, AC = 5cm, BC = 6cm. Trên tia đối của tia AB lấy điểm D sao cho AD = 5cm.
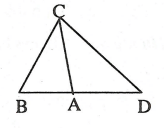 a. Tam giác ABC đồng dạng với tam giác nào ?
a. Tam giác ABC đồng dạng với tam giác nào ?
b. Tính độ dài CD.
c. Chứng minh rằng 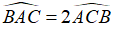 .
.
Lời giải:
a. Ta có :
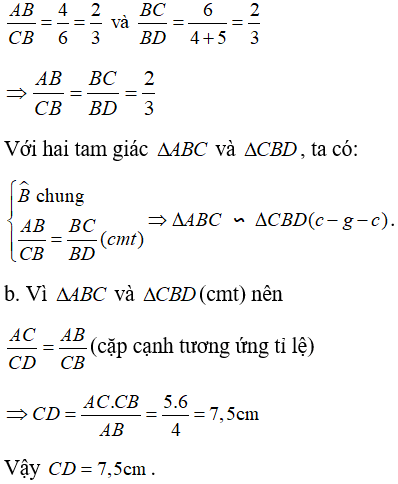

C. Bài tập tự luyện
Câu 1: Cho ΔABC có AB = 10cm, AC = 20cm. Trên cạnh AB lấy điểm D sao cho AD = 2,5 cm. Trên AC cạnh lấy điểm E sao cho AE = 5cm.
a. Tam giác ABC đồng dạng với tam giác nào?
b. Chứng minh rằng 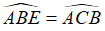 .
.
c. Tính độ dài DE, biết BE = 8cm.
Câu 2: Cho hình vẽ dưới với OA = 5cm, OC = 8cm, OD = 10cm.
Chứng minh 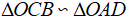
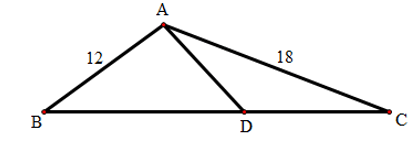
Câu 3: Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài cạnh AD.
Câu 4: Cho hình thang ABCD có AB//CD (AB//CD) và 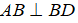 . Hai đường chéo AC và BD cắt nhau tại G. Trên đường thẳng vuông góc với AC tại C lấy điểm E sao cho CE = AG và đoạn GE không cắt đường thẳng CD. Trên đoạn CD lấy điểm F sao cho DF=GB. Chứng minh rằng
. Hai đường chéo AC và BD cắt nhau tại G. Trên đường thẳng vuông góc với AC tại C lấy điểm E sao cho CE = AG và đoạn GE không cắt đường thẳng CD. Trên đoạn CD lấy điểm F sao cho DF=GB. Chứng minh rằng
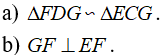
Câu 5: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chứng minh rằng:
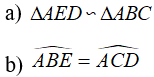
Câu 6: Cho tam giác ABC, trên phân giác trong góc A lấy điểm M sao cho 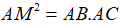 . Chứng minh rằng
. Chứng minh rằng 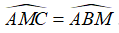 .
.
Câu 7: Cho hình thang ABCD (AB//CD) có AB = 4cm, BD = 8cm, CD = 16cm. Chứng minh rằng BC = 2AD.
Xem thêm các dạng bài tập Toán lớp 8 chọn lọc hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

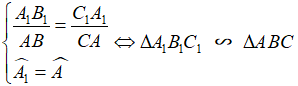
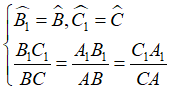

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn