Lý thuyết Đối xứng trục lớp 8 (hay, chi tiết)

Bài viết Lý thuyết Đối xứng trục lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Đối xứng trục.

Lý thuyết Đối xứng trục lớp 8 (hay, chi tiết)

Bài giảng: Bài 6: Đối xứng trục – Cô Phạm Thị Huệ Chi (Giáo viên Meraki Center)

1. Hai điểm đối xứng qua một đường thẳng

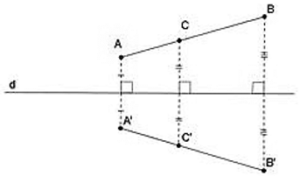
Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó

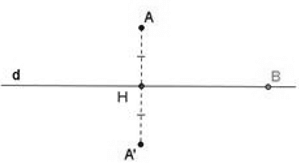
Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B.

2. Hai hình đối xứng qua đường thẳng

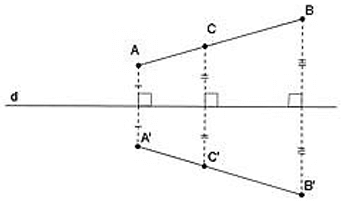
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.

Đường thẳng d gọi là trục đối xứng của hai hình đó.

3. Hình có trục đối xứng

Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.

Ta nói rằng hình H có trục đối xứng.

Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.

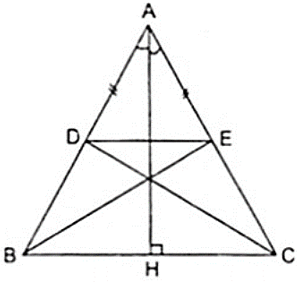
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng:

a) D đối xứng với E qua AH.

b) Δ ADC đối xứng với Δ AEB qua AH.

Lời giải:

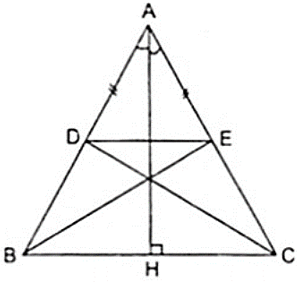
a) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.

Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE

⇒ D đối xứng với E qua AH.

b) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.

⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.

Mặt khác, ta có A đối xứng với A qua AH theo quy ước.

⇒ Δ ADC đối xứng với Δ AEB qua AH.

Bài 2: Cho Δ ABC có Aˆ
= 50⁰, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.

a) Chứng minh rằng AD = AE.

b) Tính số đo góc DAEˆ
= ?

Lời giải:

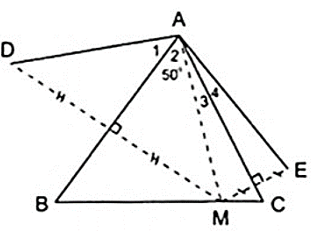
a) Theo giả thiết ta có:

+ D đối xứng với M qua AB.

+ E đối xứng với M qua AC.

+ A đối xứng với A qua AB, AC.

⇒ AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.

Áp dụng tính chất đối xứng ta có: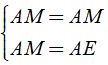
⇒ AD = AE ⇒ (đpcm).

b) Theo ý câu a, ta có

+ A₁ˆ
đối xứng A₂ˆ
qua AB

+ A₃ˆ
đối xứng A₄ˆ
qua AC.

Áp dụng tính chất đối xứng trục, ta có:

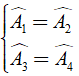
⇒ A₁ˆ
+ A₄ˆ
= A₂ˆ
+ A₃ˆ
= Aˆ
= 50⁰ ⇒ DAEˆ
= 2Aˆ
= 100⁰.

Vậy DAEˆ
= 100⁰.

Bài giảng: Bài 6: Đối xứng trục – Cô Vương Thị Hạnh (Giáo viên Meraki Center)

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

---