Cách tính đạo hàm của các hàm số đơn giản (hay, chi tiết) – Tổng hợp các dạng bài tập Toán 11 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 11.-Cách tính đạo hàm của các hàm số đơn giản (hay, chi tiết)
Cách tính đạo hàm của các hàm số đơn giản (hay, chi tiết)
Bài viết Cách tính đạo hàm của các hàm số đơn giản với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách tính đạo hàm của các hàm số đơn giản.
Cách tính đạo hàm của các hàm số đơn giản (hay, chi tiết)
Đạo hàm của các hàm số cơ bản :
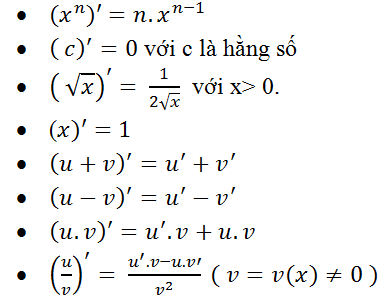
Trong đó u= u(x) ; v= v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định.
Ví dụ 1. Đạo hàm của hàm số y= 2017 là
A. 2017 B. -2017 C. 0 D. 1
Hướng dẫn giải
Hàm số y= 2017 là hàm hằng nên y’=0
Chọn C
Ví dụ 2. Cho hàm số y= f(x) = 27- 27x. Trong các mệnh đề sau, mệnh đề nào đúng?
A.f’ (x)=27 B. f'(x)= – 27 C. f’ (x)=27x D. f’ (x)=1-27x
Hướng dẫn giải
Ta có: f’ (x)=( 27-27x)’=(27)’-( 27x)’=0-27= -27
Chọn B.
Ví dụ 3. Cho hàm số y= 2x2+ 2x- 10. Tính đạo hàm của hàm số đã cho
A. 4x+ 2 B. 4x- 10
C. 2x+ 2 D. không tồn tại.
Hướng dẫn giải
Ta có: f’ (x)=( 2x2+2x-10)’=2(x2 )’+2.x’-(10)’=2.2x+2.1-0
⇒ f’(x)= 4x+ 2
Chọn A
Ví dụ 4. Đạo hàm của hàm số y= f(x)= x5 – 3x2+ 6x -10 là
A. x5– 6x + 6 B. x4– x2+ 6
C. 5x4 – 3x + 6 D. 5x4– 6x+ 6
Hướng dẫn giải
Ta có: f’ (x)=(x5-3x2+6x-10)’=(x5 )’-3(x2 )’+6.(x)’-(10)’
⇒f’(x)= 5x4 – 6x + 6
Chọn D.
Ví dụ 5. Đạo hàm của hàm số y= f(x)= (x+1)( 3- 2x) bằng biểu thức nào sau đây?
A. 3x- 2 B. 1- 4x C. 2- 4x D. 1+ 2x
Hướng dẫn giải
Áp dụng công thức: (u.v)’=u’.v+u.v’ ta có:
f’ (x)=( x+1)’.( 3-2x)+( x+1).(3-2x)’
⇒ f'(x)= 1.( 3-2x)+ (x+1). (-2) = 3- 2x- 2x- 2= 1- 4x
Chọn B.
Ví dụ 6. Đạo hàm của hàm số y=f(x)= ( x- 1)2( x- 3) bằng biểu thức nào?
A. 2x3– 2x+ 1 B.3x2– 10x + 7
C.2x2+ 5x – 7 D. 4x2 – 2x + 8
Hướng dẫn giải
+ Áp dụng công thức: (u.v)’=u’.v+u.v’ ta có:
⇒ f’ (x)=[ (x-1)2 ]’.( x-3)+(x-1)2 (x-3)’
= 2(x-1) (x-3) + (x-1)2. 1 = 2(x2 – 3x- x + 3) + x2 – 2x+ 1
= 2x2– 6x – 2x+ 6+ x2 – 2x + 1 = 3x2 – 10x + 7
Chọn B.
Ví dụ 7. Tính đạo hàm của hàm số y= (2x+1)/(x-3)?

Hướng dẫn giải
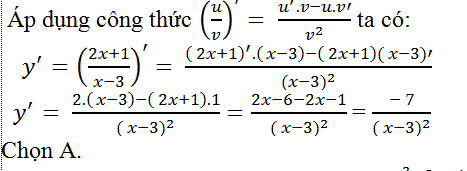
Ví dụ 8. Tính đạo hàm của hàm số y= (x2-2x-1)/(x-1)?

Hướng dẫn giải
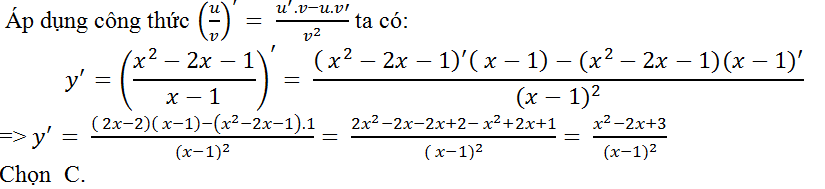
Ví dụ 9. Tính đạo hàm của hàm số: y=2√x + 2x2– 1?
A. 1/√x+4x B. 2 1/√x+4x-2 C. 1/(2√x)+4x D. Tất cả sai
Hướng dẫn giải
Ta có: y’=(2√x+2x2-1)’=2.(√x)’+2.(x2 )’-(1)’
=2.1/(2√x)+2.2x-0= 1/√x+4x
Chọn A.
Ví dụ 10. Tính đạo hàm của hàm số: y=(√x+1).( x-1)

Hướng dẫn giải
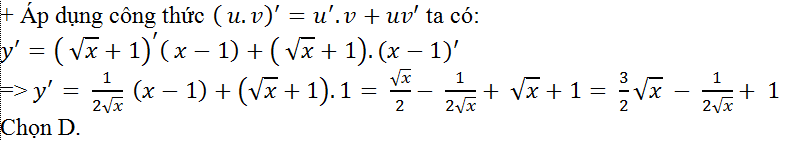
Ví dụ 11. Tính đạo hàm của hàm số: y= 2√x + 2x2 – 2x+ 10
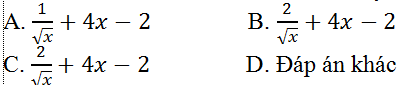
Hướng dẫn giải
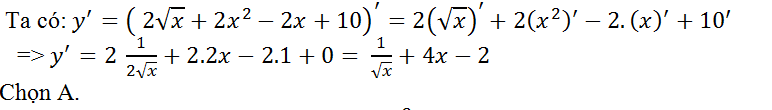
Ví dụ 12. Tính đạo hàm của hàm số y= 2/x+ x4+4x-29
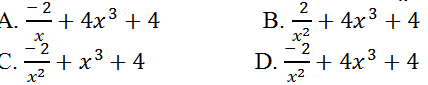
Hướng dẫn giải
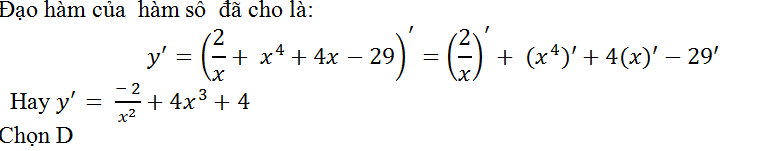
Câu 1: Đạo hàm của hàm số y= – 18√2 là:
A . – 18 B. 18 C. – 18√2 D. 0
Lời giải:
Hàm số y= – 18√2 là hàm hằng nên y’=0
Chọn D.
Câu 2: Cho hàm số y= f(x) = – 2x + 10. Trong các mệnh đề sau, mệnh đề nào đúng?
A.f’ (x)=2 B. f'(x)= – 2 C. f’ (x)=10 D. f’ (x)=-10
Lời giải:
Ta có: f’ (x)=(-2x+10)’=(-2x)’+( 10)’=-2-0= -2
Chọn B.
Câu 3: Cho hàm số y= -x2 – 7x + 8. Tính đạo hàm của hàm số đã cho
A. –x- 7 B. 2x + 7
C. 2x – 7 D. -2x- 7
Lời giải:
Ta có: f’ (x)=(-x2-7x+8)’=-(x )’-7.(x)’+(8)’=-2x-7.1+0
⇒ f’(x)= -2x – 7
Chọn D.
Câu 4: Đạo hàm của hàm số y= f(x)= 2x4 + 2x2 + x + 28 là
A. 8x3 +2x + 1 B. 8x3 +4x+ 1
C. 8x4 + 4x + 1 D. 4x3 +2x+ 1
Lời giải:
Ta có: f’ (x)=(2x4+2x2+x+28)’=2(x4 )’+2(x2 )’+(x)’+(28)’
⇒f’(x)= 8x3 +4x + 1
Chọn B.
Câu 5: Đạo hàm của hàm số y= f(x)= (x- 6)(8- 4x) bằng biểu thức nào sau đây?
A. 32- 8x B. 6x- 24 C. – 4x + 32 D. 2x+ 16
Lời giải:
Áp dụng công thức: (u.v)’=u’.v+u.v’ ta có:
f’ (x)=( x-6)’.( 8-4x)+( x-6).(8-4x)’
⇒ f'(x)= 1.( 8 – 4x)+ (x- 6). (-4) = 8- 4x – 4x + 24 = -8x + 32
Chọn A.
Câu 6: Đạo hàm của hàm số y=f(x)= (x+ 2)( x- 3) bằng biểu thức nào?
A. x+ 1 B. 2x- 1 C. 3x+ 2 D. x2– 1
Lời giải:
+ Áp dụng công thức: (u.v)’=u’.v+u.v’ ta có:
⇒ f’ (x)=(x+2)’.(x-3)+(x+2).(x-3)’
= 1.(x-3) + (x+2). 1 = x- 3+ x+ 2
= 2x – 1
Chọn B.
Câu 7: Tính đạo hàm của hàm số y= (x-6)/(2x+3)?
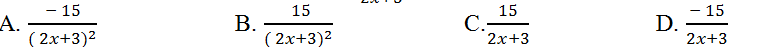
Lời giải:
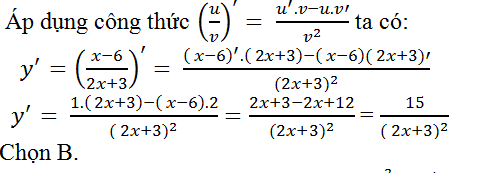
Câu 8: Tính đạo hàm của hàm số y= (x2+x+1)/(1-x)?
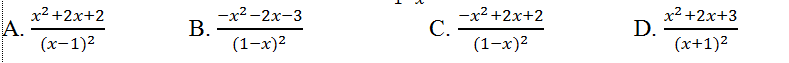
Lời giải:
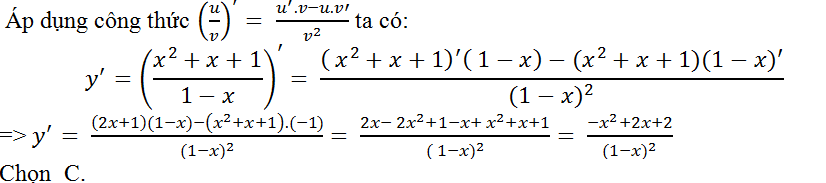
Câu 9: Tính đạo hàm của hàm số: y= (x+2)/(x2-1)?

Lời giải:
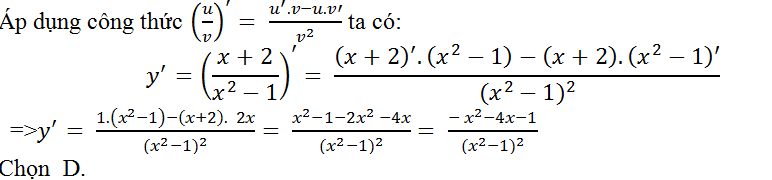
Câu 10: Tính đạo hàm của hàm số: y=4√x – 4x4 + 2x?

Lời giải:
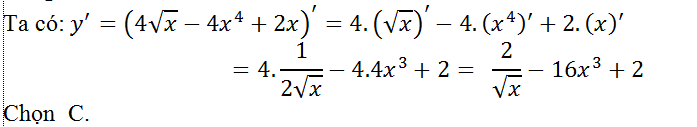
Câu 11: Tính đạo hàm của hàm số: y=(2√x-2).( 2x+1)

Lời giải:
+ Áp dụng công thức ( u.v)’=u’.v+uv’ ta có:
y’=( 2√x-2)’ ( 2x+1)+( 2√x-2).(2x+1)’
⇒ y’= 2.1/(2√x) (2x+1)+(2√x-2).2
= 2√x+ 1/√x+ 4√x-4= 6√x+ 1/√x-4
Chọn A.
Câu 12: Tính đạo hàm của hàm số y= x3/3+2x2– 1/x?
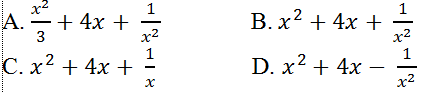
Lời giải:
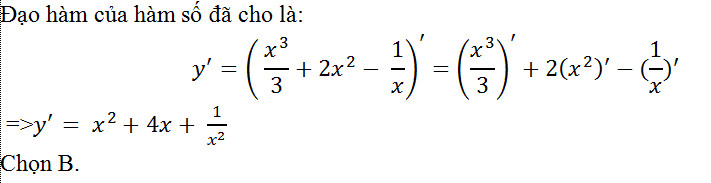
Câu 13: Tính đạo hàm của hàm số: y= (x2+2x)/(x2-3x+1)

Lời giải:
Áp dụng công thức đạo hàm của một thương ta có:
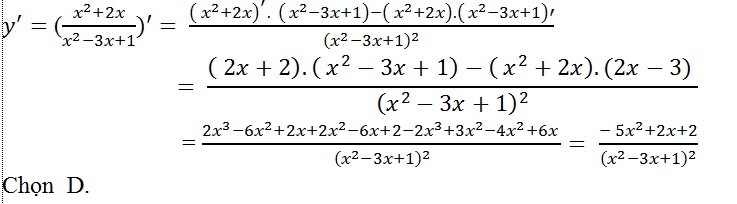
Bài 1. Đạo hàm của hàm số y = f(x) = (x2 + x + 1)(x – 5).
Bài 2. Tính đạo hàm của hàm số y = (x + 5)2(x – 9).
Bài 3. Tính đạo hàm của hàm số y = x−1x+1.
Bài 4. Tính đạo hàm của hàm số y = 1x−32x+1.
Bài 5. Tính đạo hàm của hàm số f(x) = 13x+3.2x−2.

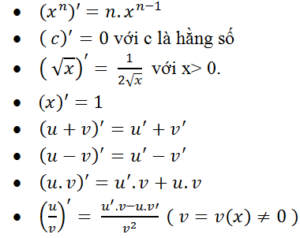

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn