Tìm tập xác định của hàm số lượng giác lớp 11 (cách giải + bài tập) – Chuyên đề các dạng bài tập Toán 11 sách mới với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 11.-Tìm tập xác định của hàm số lượng giác lớp 11 (cách giải + bài tập)
Tìm tập xác định của hàm số lượng giác lớp 11 (cách giải + bài tập)
Chuyên đề phương pháp giải bài tập Tìm tập xác định của hàm số lượng giác lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện
đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tìm tập xác định của hàm số lượng giác.
Tìm tập xác định của hàm số lượng giác lớp 11 (cách giải + bài tập)
1. Phương pháp giải
* Tập xác định của hàm số lượng giác
– Hàm số y = sin x, y = cos x xác định trên ℝ.
Khi đó, y = sin[u(x)], y = cos [u(x)] xác định khi và chỉ khi u(x) xác định.
– Hàm số y = tan x có tập xác định là 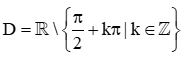 .
.
Khi đó, y = tan [u(x)] có nghĩa khi và chỉ khi u(x) xác định và ux≠π2+kπ, k∈ℤ.
– Hàm số y = cot x có tập xác định là D = ℝ {kπ | k ∈ ℤ}.
Khi đó, y = cot [u(x)] có nghĩa khi và chỉ khi u(x) xác định và u(x) ≠kπ, k ∈ ℤ.
* Một số chú ý khi tìm điều kiện xác định:
– Hàm số y=f(x)xác định khi f(x) ≥ 0.
– Hàm số y=1f(x) xác định khi f(x) ≠ 0.
– Hàm số y=1f(x) xác định khi f(x) > 0.
– Một số trường hợp đặc biệt:
sinx≠0⇔x≠kπ,k∈ℤ;
cosx≠0⇔x≠π2+kπ,k∈ℤ;
sinx≠±1⇔x≠±π2+k2π,k∈ℤ;
cosx≠1⇔x≠k2π,k∈ℤ;
cosx≠−1⇔x≠π+k2π,k∈ℤ.
2. Ví dụ minh họa
Ví dụ 1.Tìm tập xác định của các hàm số sau:
a) y=tanx−π6;
b) y=cot−2x−π3;
c) y=sin2x+1sin4x−1;
d) y=2cosx2−3x+2.
Hướng dẫn giải:
a) Biểu thức tanx−π6 có nghĩa khi cosx−π6≠0, tức là x−π6≠π2+kπk∈ℤ.
Hay x≠2π3+kπk∈ℤ.
Vậy tập xác định của hàm số đã cho là 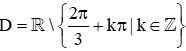 .
.
b) Biểu thức cot−2x−π3 có nghĩa khi và chỉ khi −2x−π3≠kπ k∈ℤ, tức là x≠−π6−kπ2 k∈ℤ.
Tập xác định của hàm số là 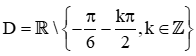 .
.
c) Biểu thức sin2x+1sin4x−1 có nghĩa khi sin 4x ≠ 1, tức là 4x≠π2+k2πk∈ℤ.
Hay x≠π8+kπ2k∈ℤ.
Vậy tập xác định của hàm số đã cho là 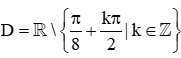 .
.
d) Biểu thức 2cosx2−3x+2 có nghĩa khi x2 – 3x + 2 ≥ 0, tức là x ≤ 1 hoặc x ≥ 2.
Vậy tập xác định của hàm số đã cho là D = (–∞; 1] ∪ [2; +∞).
Ví dụ 2. Tìm m để hàm số y=5−msinx−m+1cosx xác định trên ℝ.
Hướng dẫn giải:
Hàm số xác định trên ℝ khi chỉ khi 5 – m sin x – (m + 1) cos x ≥ 0, ∀x ∈ ℝ
⇔ m sin x + (m + 1) cos x ≤ 5, ∀x ∈ ℝ
⇔mm2+m+12sinx+m+1m2+m+12cosx≤5m2+m+12 , ∀x∈ℝ
⇔sinx+α≤5m2+m+12 , ∀x∈ℝ(với α thỏa mãn cosα=mm2+m+12)
⇔52m2+2m+1≥1⇔2m2+2m+1≤5
⇔2m2+2m−24≤0⇔−4≤m≤3.
Vậy m ∈ [– 4; 3] thì thỏa mãn yêu cầu bài toán.
3. Bài tập tự luyện
Bài 1. Tập xác định của hàm số y = 2023tan2024 2x là
A. 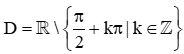 ;
;
B. 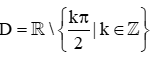 ;
;
C. 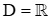 ;
;
D. 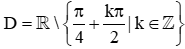 .
.
Bài 2. Hàm số y = cot2a + 2cosa + 3 có tập xác định là
A. 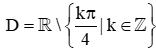 ;
;
B. 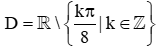 ;
;
C. 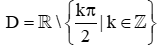 ;
;
D. 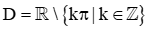 .
.
Bài 3. Tập xác định của hàm số y = 2cotx + sin3x là
A. 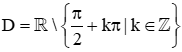 ;
;
B. 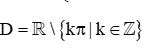 ;
;
C. 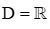 ;
;
D. 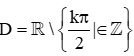 .
.
Bài 4. Tập xác định của hàm số y=tanx+2π3 là
A. 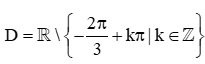 ;
;
B.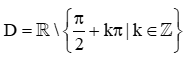 ;
;
C. 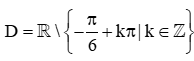 ;
;
D. 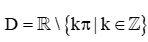 .
.
Bài 5. Tập xác định của hàm số y=1sin2x−cos2x là
A. 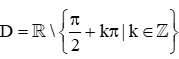 ;
;
B. 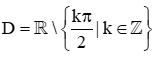 ;
;
C. 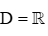 ;
;
D.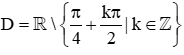 .
.
Bài 6. Tập nào sau đây là tập xác định của hàm số y=cotxsinx−1 ?
A. 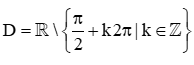 ;
;
B. 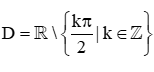 ;
;
C. 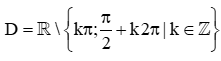 ;
;
D. 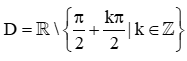 .
.
Bài 7. Xét bốn mệnh đề sau:
(1) Hàm số y = sin x có tập xác định là ℝ.
(2) Hàm số y = cos x có tập xác định là ℝ.
(3) Hàm số y = tan x có tập xác định là ℝ{kπ}.
(4) Hàm số y = cot x có tập xác định là 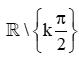 .
.
Số mệnh đề đúng trong các mệnh đề trên là
A. 1;
B. 2;
C. 3;
D. 4.
Bài 8. Hàm số y=2+cosxsin3x có tập xác định là
A. 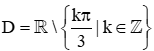 ;
;
B. 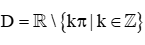 ;
;
C. 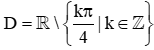 ;
;
D. 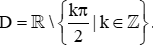 .
.
Bài 9. Hàm số nào sau đây có tập xác định là ℝ?
A. y=2cosx;
B. y=tan2xsin2x+1;
C. y=cos1x;
D. y=sin2x+3cos4x+5.
Bài 10. Giá trị của m để hàm số y=2−sin2xmcosx+1 xác định trên ℝ là
A. –1 ≤ m ≤ 1;
B. –1 < m < 1;
C. m > 0;
D. 0 < m < 1.
Bài 11. Tập hợp tất cả giá trị của m để hàm số y=1sin2x−m có tập xác định là ℝ là
A. [–1; 1];
B. (– ∞; –1) ∪ (1; + ∞);
C. (–1; 1);
D. (– ∞; –1] ∪ [1; + ∞).
Xem thêm các dạng bài tập Toán 11 hay, chi tiết khác:

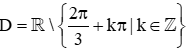
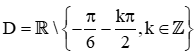

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn