Lý thuyết Hàm số liên tục lớp 11 (hay, chi tiết)

---

---

Bài viết Lý thuyết Hàm số liên tục lớp 11 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hàm số liên tục.

Lý thuyết Hàm số liên tục

Bài giảng: Bài 3: Hàm số liên tục – Thầy Lê Thành Đạt (Giáo viên Meraki Center)

Định nghĩa 1

    Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

    Hàm số y = f(x) được gọi là liên tục tại x₀ nếu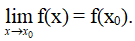

Định nghĩa 2

    Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

    Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và

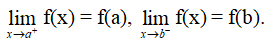
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

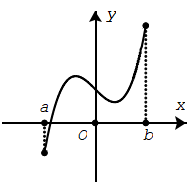
Hàm số liên tục trên khoảng (a;b)

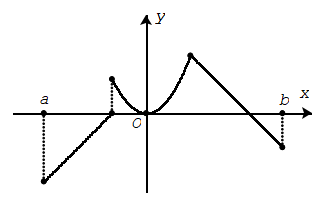
Hàm số không liên tục trên khoảng (a; b).

Định lí 1

    a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.

    b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

    Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

    a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

    b) Hàm số 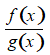liên tục tại x₀ nếu g(x₀) ≠ 0.

Định lí 3

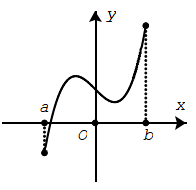
    Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..

Định lí 3 có thể phát biểu theo một dạng khác như sau:

    Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).

Xem thêm các bài lý thuyết Toán lớp 11 chi tiết khác:

---

---

---