Bài tập Tọa độ của vecto, tọa độ của một điểm (cực hay, chi tiết)

---

---

Bài viết Bài tập Tọa độ của vecto, tọa độ của một điểm với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Bài tập Tọa độ của vecto, tọa độ của một điểm.

Bài tập Tọa độ của vecto, tọa độ của một điểm (cực hay, chi tiết)

Để làm dạng bài tập này, ta phải nắm vững công thức tọa độ vecto, tọa độ của một điểm và mối liên hệ giữa tọa độ điểm và tọa độ vecto.

Tọa độ của vecto:

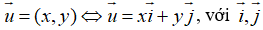là các vecto đơn vị,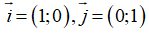

Hai vecto bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau. Nếu có 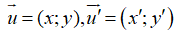thì .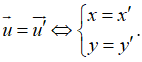

Cho hai vecto 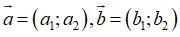. Khi đó ta có

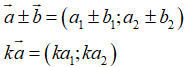
Tọa độ của điểm: Trong mặt phẳng tọa độ Oxy, tọa độ của vecto 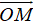được gọi là tọa độ điểm M

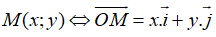
Mối liên hệ: Cho hai điểm A(x_A; y_A), B(x_B; y_B). Khi đó ta có

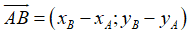
Ví dụ 1: Tìm tọa độ các vecto sau:

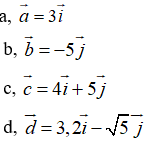
Hướng dẫn giải:

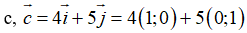
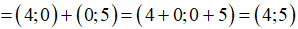
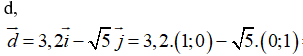
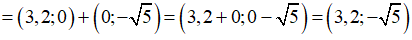
Ví dụ 2: Cho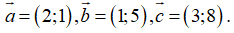

a, Tìm tọa độ của vecto .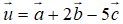

b, Tìm tọa độ vecto sao cho .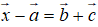

c, Tìm các số m, n để .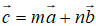

Hướng dẫn giải:

Ta có:

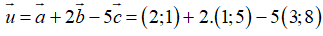
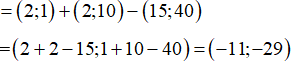
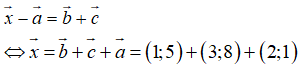
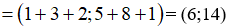
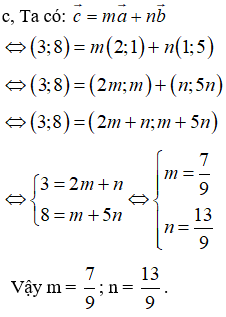
Ví dụ 3: Vecto 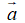= (2; -1) biểu diễn dưới dạng 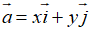được kết quả nào sau đây?

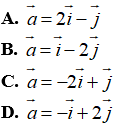
Hướng dẫn giải:

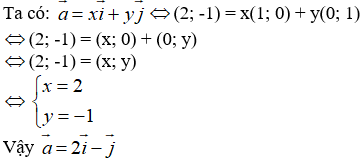
Đáp án A

Ví dụ 4: Ví dụ 4. Trong hệ trục tọa độ Oxy, cho các điểm A(m; n), B(-2; 7) và 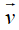= (-4; 9). Giá trị của m và n để .

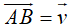A. m = -2 và n = 2

B. m = 2 và n = -2

C. m = -6 và n = 16

D. m= 6 và n = -16

Hướng dẫn giải:

Ta có:

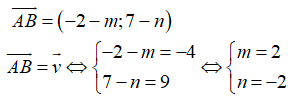
Đáp án B

Ví dụ 5: Ví dụ 5. Trong hệ trục tọa độ Oxy, cho tọa độ các điểm M(3; -6); N(-10; 5) và Q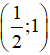. Tìm tọa độ điểm K để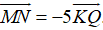

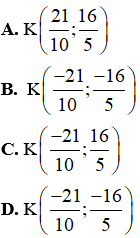
Hướng dẫn giải:

Ta có: 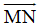= (-10 – 3,5 – (-6)) = (-13; 11)

Gọi tọa độ điểm K(x; y). Khi đó ta có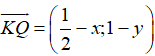

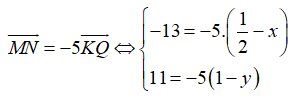
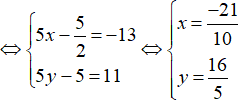
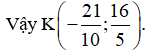
Đáp án C

Bài 1. Trên trục tọa độ (O; i→) cho 2 điểm A, B có tọa độ lần lượt là –5; 3. Tìm tọa độ của vectơ AB→ và tọa độ trung điểm I của đoạn thẳng AB.

Hướng dẫn giải:

Ta có: AB→ = x_B – x_A = 3 – (–5) = 8.

Suy ra AB→=8i→.

Khi đó, tọa độ của vectơ AB→ trên trục tọa độ (O; i→) là 8.

Do đó, tọa độ điểm I là: xI=xA+xB2=(-5)+32=-1.

Bài 2.  Trong mặt phẳng Oxy, cho 3 điểm A (–9; 5), B (3; 5) và C (–10; –8). Tìm tọa độ trọng tâm G của tam giác ABC, tọa độ trung điểm đoạn thẳng AB, AC.

Hướng dẫn giải:

+) Áp dụng công thức tọa độ trọng tâm tam giác ta có:

• xG=xA+xB+xC3=-9+3-103=-163;

• yG=yA+yB+yC3=5+5-83=23.

Do đó G-163;23.

+) Áp dụng công thức tọa độ trung điểm đoạn thẳng ta có:

Gọi I là trung điểm của đoạn thẳng AB có:

• xI=xA+xB2=-9+32=-3;

• yI=yA+yB2=5+52=5.

Do đó I(-3;5).

Gọi J là trung điểm của đoạn thẳng AC có:

• xJ=xA+xC2=-9-102=-192

• yJ=yA+yC2=5-82=-32

Do đó J-192;-32.

Bài 3. Cho hai vectơ u→ = (–1; –2) và v→ = (–6; –5) . Tính tọa độ các vectơ u→+v→, u→-v→, ku→ với k = 5.

Hướng dẫn giải:

+) Ta có: u→+v→= (u₁ + v₁; u₂ + v₂) = (–1 –6 ; –2 – 5 ) = (–7; –7).

+) Ta có: u→-v→= (u₁ – v₁; u₂ – v₂) = (–1 + 6; –2 + 5 ) = (5; 3).

+) Ta có: ku→= (ku₁; ku₂) = (5.(–1); 5.(–5)) = (–5; –25).

Bài 4. Cho các vectơ a→= (–3; 2), b→= (4; 1) và c→= (10; –9). Phân tích vectơ b→ theo hai vectơ a→ và c→.

Hướng dẫn giải:

Giả sử b→=xa→+yc→⇒4=-3x+10y1=2x-9y⇒x=-467y=-117.

⇒b→=-467a→-117c→

Bài 5. Cho A (–2; 1), B (–3; 7). Điểm M nằm trên trục Oy sao cho ba điểm A, B, M thẳng hàng. Tìm tọa độ điểm M .

Hướng dẫn giải:

Ta có: M nằm trên trục Oy ⇒ M = (0; y)

Ba điểm A, B, M thẳng hàng nên AB→ cùng phương với AM→.

-3-1=4y-2

4y-2=3

3y – 6 = 4

y=103

Do đó M0;103.

Bài 6. Trong mặt phẳng Oxy, cho hình vuông ABCD tâm I và có A (2; 1). Biết điểm B thuộc trục Ox và BC→ cùng hướng với i→. Tìm tọa độ vectơ AC→.

Bài 7. Trong mặt phẳng Oxy, cho các điểm A (–9; –6) , B (2; 0), C (3; 0). Tìm tọa độ điểm M thỏa mãn: 3MA→-BC→=2CM→.

Bài 8. Trong mặt phẳng Oxy, cho A (m – 3; 2), B (3; 5 – 3m), C (2m + 1; 2). Tìm m để A, B, C là ba điểm thẳng hàng.

Bài 9. Trong mặt phẳng tọa độ Oxy, u→=(3;7). Hãy biểu diễn vectơ u→ qua vectơ i→ và j→.

Bài 10. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(–2; 3), B(0; 5). Tìm điểm M(x; y) để OABM là một hình bình hành.

Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:

Lời giải bài tập lớp 10 sách mới:

---

---

---