Lý thuyết Tính chất ba đường cao của tam giác lớp 7 (hay, chi tiết)

Bài viết Lý thuyết Tính chất ba đường cao của tam giác lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Tính chất ba đường cao của tam giác.

Lý thuyết Tính chất ba đường cao của tam giác lớp 7 (hay, chi tiết)

1. Đường cao của tam giác

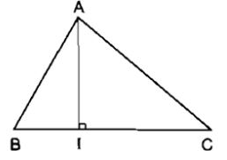
• Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

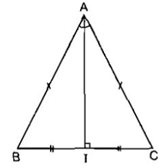
Ví dụ: Đoạn thẳng AI là một đường cao của tam giác ABC, còn nói AI là đường cao xuất phát từ đỉnh A (của tam giác ABC).

• Mỗi tam giác có ba đường cao.

2. Tính chất ba đường cao của một tam giác

Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.

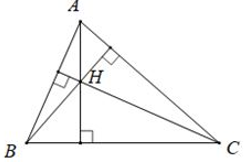
Ví dụ: H là giao điểm ba đường cao của tam giác ABC. H là trực tâm của tam giác ABC

3. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân

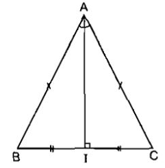
Tính chất của tam giác cân: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.

Nhận xét:

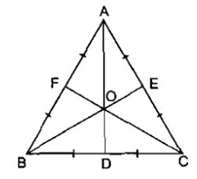
Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó là một tam giác cân

Đặc biệt đối với tam giác đều, từ tính chất trên suy ra: Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.

4. Ví dụ

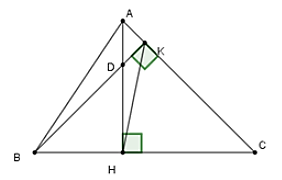
Ví dụ :Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D. Biết 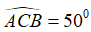, tính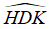

Lời giải:

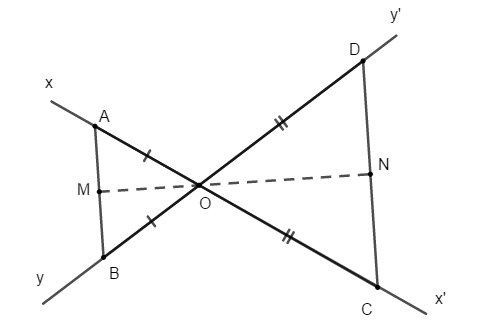
Bài 1: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Trên Ox và Ox’ lần lượt lấy các điểm A và C; trên Oy và Oy’ lần lượt lấy các điểm B, D sao cho OA = OA, OC = OD. Gọi M, N lần lượt là trung điểm của AB, CD

Chứng minh M, O, N thẳng hàng.

Lời giải:

Bài 2:Cho tam giác ABC cân tại A. Qua A kẻ đường thẳng d song song với đáy BC. Các đường phân giác của góc B và góc C lần lượt cắt d tại E và F. Chứng minh rằng:

a) d là phân giác ngoài của góc A

b) AE = AF

Lời giải:

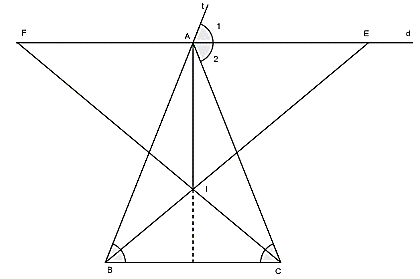
b) Gọi I là giao điểm của hai tia phân giác CF và BE trong tam giác ABC

Nên I là giao điểm của ba đường phân giác trong tam giác ABC

Suy ra AI là tai phân giác của góc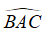

Mà tam giác ABC cân tại A

Nên AI là đường trung trực ứng với cạnh BC của tam giác ABC

Bài 1. Cho ∆ABC có A^ > 90^o, AD vuông góc với BC tại D, BE vuông góc với AC tại E. Gọi F là giao điểm của đường thẳng AD và BE. Chứng minh AB ⊥ FC.

Hướng dẫn giải

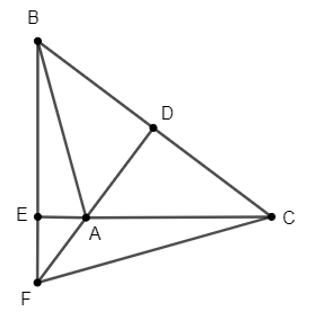
Xét ∆FBC có AD ⊥ BC nên FD ⊥ BC (1)

BE ⊥ AC ⇒ CE ⊥ BF (2)

Từ (1) và (2) suy ra CE và FD là đường cao của ∆FBC.

Mà {A} = FD ∩ CE nên A là trực tâm ∆FBC,

Suy ra A thuộc đường cao hạ từ B của ∆FBC ⇒ AB ⊥ PC.

Bài 2. Cho ∆ABC có 3 góc nhọn (AB < AC), đường cao AH. Lấy D là điểm thuộc đoạn HC, vẽ DE ⊥ AC (E ∈ AC). Gọi K là giao điểm của AH và DE. Chứng minh AD ⊥ KC.

Hướng dẫn giải:

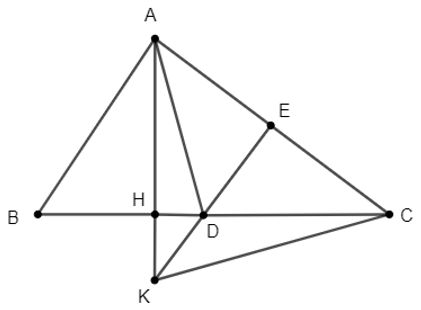
Xét ∆AKC ta có: AH ⊥ BC ⇒ CH ⊥ AK. (1)

Và DE ⊥ AC ⇒ KE ⊥ AC.

Từ (1) và (2) suy ra KE và CH là hai đường cao của ∆AKC.

Mà {D} = KE ∩ CH nên D là trực tâm của ∆AKC

⇒ D thuộc đường cao hạ từ A của ∆AKC ⇒ AD ⊥ KC.

Bài 3. Cho ∆ABC có A^ >90^o , AD vuông góc với BC tại D, BE vuông góc với AC tại E. Gọi F là giao điểm của đường thẳng AD và BE. Chứng minh AB ⊥ FC.

Hướng dẫn giải:

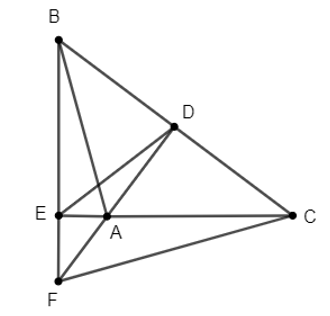
Xét ∆FBC có AD ⊥ BC nên FD ⊥ BC. (1)

BE ⊥ AC ⇒ CE ⊥ BF.

Từ (1) và (2) suy ra CE và FD là các đường cao của ∆FBC.

Mà {A} = FD ∩ CE nên A là trực tâm ∆FBC.

Suy ra A thuộc đường cao hạ từ B của ∆FBC ⇒ AB ⊥ FC.

Bài 4. Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N; từ C kẻ đường thẳng vuông góc với BM tại P. Chứng minh ba đường thẳng AB, CP, MN cùng đi qua một điểm.

Hướng dẫn giải:

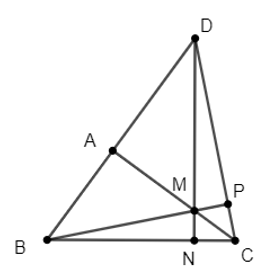
Gọi D là giao điểm của các đường thẳng AB và CP.

Xét ∆DBC ta có:

AB ⊥ AC ⇒ AC ⊥ BD, (1)

CP ⊥ BP ⇒ BP ⊥ DC (2)

Từ (1) và (2) suy ra CA và BP là các đường cao của ∆DBC.

Mà {M} = BP ∩ CA nên M là trực tâm ∆DBC ⇒ DM ⊥ BC.

Lại có MN ⊥ BC nên M, N, D thẳng hàng ⇒ AB, MN và CP cùng đi qua điểm D.

Bài 5. Cho ∆ABC có BD và CE lần lượt là các đường cao hạ từ B, C và BD = CE. H là giao điểm của BD và CE. Chứng minh rằng ∆ABC cân và AH là phân giác BAC^.

Hướng dẫn giải:

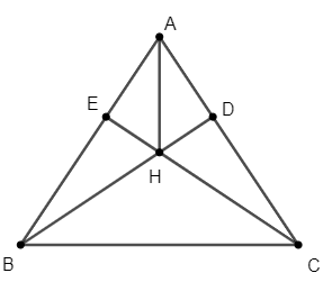
Xét ∆DBA và ∆ECA có:

CEA^=ECA^=90o;

CE = BD (gt);

 A^ là góc chung.

Do đó ∆DBA = ∆ECA (g.c.g)

Suy ra AB = AC (hai cạnh tương ứng)

Do đó ∆ABC cân tại A.

Xét ∆ABC có BD ⊥ AC, CE ⊥ AB.

Mà H là giao điểm của CE và BD nên H là trực tâm của ∆ABC.

Suy ra AH là đường cao của ∆ABC.

Mà  ∆ABC cân tại A nên AH là phân giác của BAC^.

Bài 6. Cho ∆ABC cân tại A, có C^=70o, đường cao BH cắt đường trung tuyến AM (M ∈ BC) ở K. Chứng minh CK ⊥ AB và tính HKM^.

Bài 7. Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh ED ⊥ BC.

Bài 8. Cho ∆ABC vuông tại A, đường cao AH, phân giác AD. Gọi I, J lần lượt là giao điểm các đường phân giác trong của ∆ABH, ∆ACH. E là giao điểm của đường thẳng BI với A. Chứng minh rằng:

a) ∆ADE là tam giác vuông.

b) IJ ⊥ AD.

Bài 9. Cho ∆ABC, có A^=100o, C^=30o; đường cao AH. Trên cạnh AC lấy điểm D sao cho CBD^=10o. Vẽ đường phân giác của BAD^ cắt BD ở E. Chứng minh rằng AE ⊥ BD.

Bài 10. Cho ∆ABC nhọn, có AH ⊥ BC (H ∈ BC). Trên AH lấy điểm D sao cho HAB^=HCD^. Chứng minh BD ⊥ AC.

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:

Lời giải bài tập lớp 7 sách mới:

---