Cách phân tích đa thức ax^2 + bx + c thành nhân tử để giải phương trình bậc hai – Chuyên đề Toán 9 tổng hợp phương pháp giải các dạng bài tập Toán 9 hay, chi tiết giúp bạn học tốt Toán 9.-Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai
Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai
Bài viết Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai.
Cách phân tích đa thức ax2 + bx + c thành nhân tử để giải phương trình bậc hai
Cách 1: Đặt nhân tử chung
– Sử dụng trong trường hợp c = 0, khi đó ta có ax2 + bx = x(ax + b)
Ví dụ: Phân tích biểu thức sau thành nhân tử
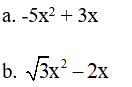
Giải
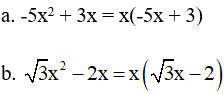
Cách 2: Dùng hằng đẳng thức A2 – B2
– Sử dụng trong trường hợp b = 0 và c < 0, khi đó ta có:
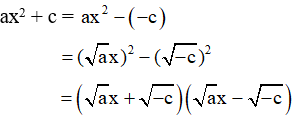
Ví dụ: Phân tích biểu thức sau thành nhân tử
a. 9x2 – 16
b. 3x2 – 2
Giải
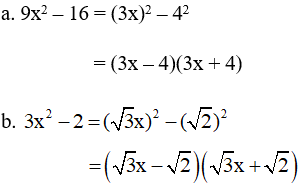
Cách 3: Tách số hạng bx thành hai số hạng rồi nhóm các hạng tử và đặt nhân tử chung
-bổ sung- Để tách bx thành hai hạng tử ta làm như sau:
+ B1: Tìm tích ac, phân tích ac thành tích hai thừa số nguyên
+ B2: Chọn hai thừa số có tổng bằng b
Ví dụ: Phân tích biểu thức sau thành nhân tử
a. 4x2 – 4x – 3
b. x2 – 12x + 27
Giải
a. Tích ac = -12 = (-1).12 = (-12).1 = 2.(-6) = (-2).6
Trong các cặp số trên ta chọn cặp số 2 và -6 vì tổng của chúng bằng -4 = b
⇒ -4x = -6x + 2x
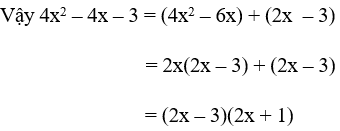
b. Tích ac = 27 = 1.27 = (-1).(-27) = 3.9 = (-3).(-9)
Trong các cặp số trên ta chọn cặp số -3 và -9 vì tổng của chúng bằng -12 = b
⇒ -12x = -3x – 9x
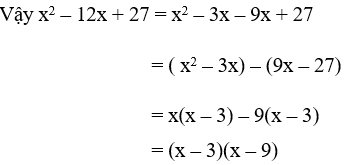
Cách 4: Tách số hạng (ax2 hoặc c) thành hai số hạng rồi đưa biểu thức
ax2 + bx +c về dạng A2 – B2
Ví dụ: Phân tích biểu thức sau thành nhân tử
a. 4x2 – 4x – 3
b. 3x2 – 8x + 4
Giải
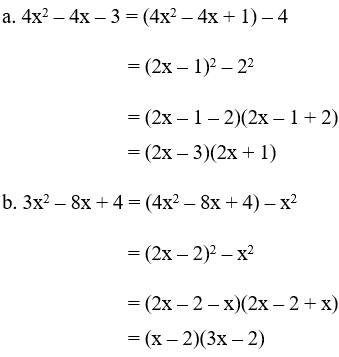
Cách 5: Sử dụng nghiệm của phương trình bậc hai
– Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 thì:
ax2 + bx + c = a(x – x1)(x – x2)
Ví dụ: Phân tích biểu thức sau thành nhân tử
a. 2x2 – 7x + 3
b. 5x2 + 24x + 19
Giải
a. Xét phương trình 2x2 – 7x + 3 = 0 có: Δ = b2 – 4ac = (-7)2 – 4.2.3 = 25 > 0
Do đó phương trình có 2 nghiệm phân biệt: x1 = 3, x2 = 1/2
Vậy 2x2 – 7x + 3 = 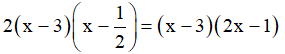
b. Xét phương trình 5x2 + 24x + 19 = 0 có: Δ = b2 – 4ac = (24)2 – 4.5.19 = 196 > 0
Do đó phương trình có 2 nghiệm phân biệt: x1 = -1, x2 = 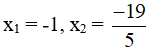
Vậy 5x2 + 24x + 19 = 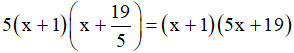
Câu 1: Khi phân tích biểu thức x2 – 11x + 30 thành nhân tử ta được kết quả là
A. (x – 5)(x – 6)
B. (x + 5)(x + 6)
C. (x – 3)(x – 10)
D. (x – 2)(x – 15)
Giải
Tích ac = 30 = (-5).(-6) = 5.6 = 2.15 = (-2).(-15) = 3.10 = (-3).(-10)
Trong các cặp số trên ta chọn cặp số -5 và -6 vì tổng của chúng bằng -11 = b
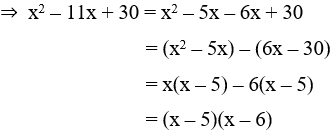
Đáp án A
Câu 2: Khi phân tích biểu thức 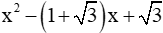 thành nhân tử ta được kết quả là
thành nhân tử ta được kết quả là
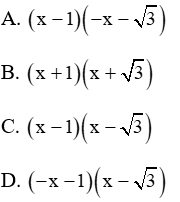
Giải
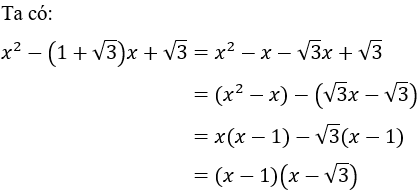
Đáp án C
Câu 3: Khi phân tích biểu thức x2 – 10x + 21thành (x + a)(x + b) thì tổng của a và b bằng bao nhiêu
A. -9
B. -10
C. -11
D. -12
Giải
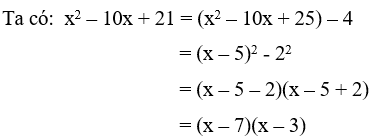
Vậy a + b = -7 – 3 = -10
Đáp án B
Câu 4: Khi phân tích biểu thức 4x2 – 8x + 3 thành (ax + b)(cx + d) thì tích của b và d bằng bao nhiêu
A. 1
B. 2
C. 3
D. 4
Giải
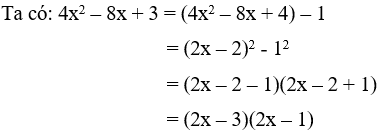
Vậy tích bd = (-3).(-1) = 3
Đáp án C
Câu 5: Khi phân tích biểu thức 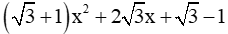 thành nhân tử thì một trong hai nhân tử là
thành nhân tử thì một trong hai nhân tử là
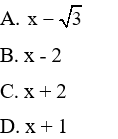
Giải
Xét phương trình 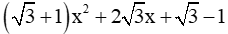 = 0 có:
= 0 có:
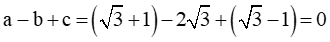
Do đó phương trình có 2 nghiệm phân biệt: 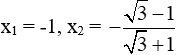
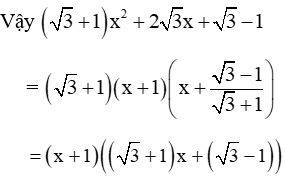
Vậy đáp án D
Câu 6: Khi phân tích biểu thức 9x2 + 12x – 5 thành nhân tử thì một trong hai nhân tử là
A. x – 7
B. x – 2
C. 3x + 2
D. 3x + 5
Giải
Tích ac = -45 = (-5).9 = 5.(-9) = (-3).15 = 3.(-15) = 1.(-45) = (-1).45
Trong các cặp số trên ta chọn cặp số -3 và 15 vì tổng của chúng bằng 12 = b
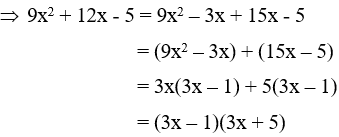
Đáp án D
Câu 7: Kết quả phân tích biểu thức x2 + 7x + 12 thành nhân tử là
A. (x + 1)(x + 12)
B. (x + 3)(x + 4)
C. (x – 3)(x – 4)
D. (x – 1)(x – 12)
Giải
Xét phương trình x2 + 7x + 12 = 0
Phương trình có ∆ = 72 – 4.1.12 = 49 – 48 = 1 > 0 nên có hai nghiệm phân biệt
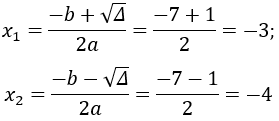
⇒ x2 + 7x + 12 = (x + 3)(x + 4)
Đáp án B
Câu 8: Biểu thức nào sau đây có kết quả phân tích thành nhân tử là (3x – 2)(-x + 7)
A. -3x2 + 13x – 14
B. -3x2 + 33x – 14
C. -3x2 + 23x – 14
D. -3x2 + 3x – 14
Giải
Ta có (3x – 2)(-x + 7) = -3x2 + 21x + 2x -14 = -3x2 + 23x – 14
Đáp án C
Bài 1. Phân tích các đa thức sau thành nhân tử
a) x2 – 7x + 6;
b) 2x-5x+3;
c) (2-3)x2+23x-(2+3).
Bài 2. Bạn Hoàng đưa ra khẳng định: “Đa thức 4x-7x+3 được phân tích thành (x – 1)(4x – 3)”. Theo em, khẳng định trên là đúng hai sai, nếu sai hãy sửa lại.
Bài 3. Điền vào chỗ chấm sau.
a) – 3x2 – 2x + 5 = (x – 1)( … );
b) 4x2 – 25x + 6 = ( … )(x – 6);
c) 4x2 – 5x + 1 = ( … )( … ).
Bài 4. Cho đa thức sau: (2x-2)2-1-(x+1)(x-1)
a) Thực hiện thu gọn đa thức;
b) Phân tích đa thức vừa thu gọn thành nhân tử.
Bài 5. Cho đa thức 5×2-(2-5)x-2 được phân tích thành (ax + b)(cx + d). Hãy tính a + b + c + d?
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

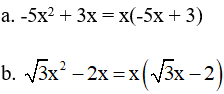
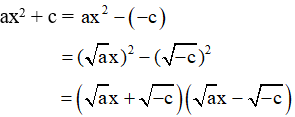

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn