Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn lớp 9 (cực hay, có đáp án) – Chuyên đề Toán 9 tổng hợp phương pháp giải các dạng bài tập Toán 9 hay, chi tiết giúp bạn học tốt Toán 9.-Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn lớp 9 (cực hay, có đáp án)
Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn lớp 9 (cực hay, có đáp án)
Bài viết Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn.
Hệ thức vi-et và ứng dụng để giải phương trình bậc hai một ẩn lớp 9 (cực hay, có đáp án)
Định lý Vi-ét: Nếu phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 (phân biệt hoặc trùng nhau) thì tổng các nghiệm 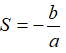 và tích các nghiệm
và tích các nghiệm 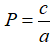 .
.
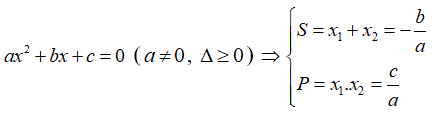
Dạng 2.1: Tìm tham số m để phương trình có nghiệm thỏa mãn điều kiện cho trước
Bước 1: Tìm điều kiện để phương trình có nghiệm.
Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.
Bước 3: Sử dụng hệ thức Vi-ét, kết hợp biến đổi đẳng thức, bất đẳng thức để tìm tham số.
Bước 4: Đối chiếu điều kiện và kết luận.
Dạng 2.2: Tìm tham số và tìm nghiệm còn lại khi biết trước một nghiệm x0 của phương trình.
Bước 1: Thay giá trị x0 vào phương trình để tìm tham số.
Bước 2: Thay giá trị của tham số hệ thức Vi-ét để tìm nghiệm còn lại.
Bước 3: Kết luận.
Dạng 2.3: Khi phương trình bậc hai có nghiệm, tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số.
Bước 1: Tìm điều kiện để phương trình có nghiệm.
Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.
Bước 3: Tính m theo S và P.
Bước 4: Khử m và tìm ra hệ thức.
Bước 5: Kết luận.
Dạng 2.4. Áp dụng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình bậc hai
Cho phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0).
+) Nếu a + b + c = 0 thì phương trình có nghiệm x1 = 1 và x2 = 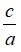 .
.
+) Nếu a – b + c = 0 thì phương trình có nghiệm x1 = -1 và x2 = 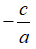 .
.
Dạng 2.5. Tìm hai số khi biết tổng và tích
Nếu hai số u và v có tổng u + v = S và tích u.v = P thì hai số đó là nghiệm của phương trình x2 – Sx + P = 0 .
Điều kiện để có u và v là S2 – 4P ≥ 0.
Ví dụ 1: Cho phương trình bậc hai (m – 1)x2 – 2mx + m + 1 = 0 (m là tham số). Các giá trị nguyên của m để phương trình có nghiệm nguyên là:

Lời giải
Chọn A

Ví dụ 2: Phương trình x2 + (2m + 1)x + 3m = 0 (với m là tham số) có hai nghiệm phân biệt, trong đó có một nghiệm là x1 = 3, nghiệm còn lại là x2 bằng:

Lời giải
Chọn D

Ví dụ 3: Tìm hệ thức liên hệ giữa hai nghiệm của phương trình x2 – (m + 3)x + 2m – 5 = 0 không phụ thuộc vào m.

Lời giải
Chọn A
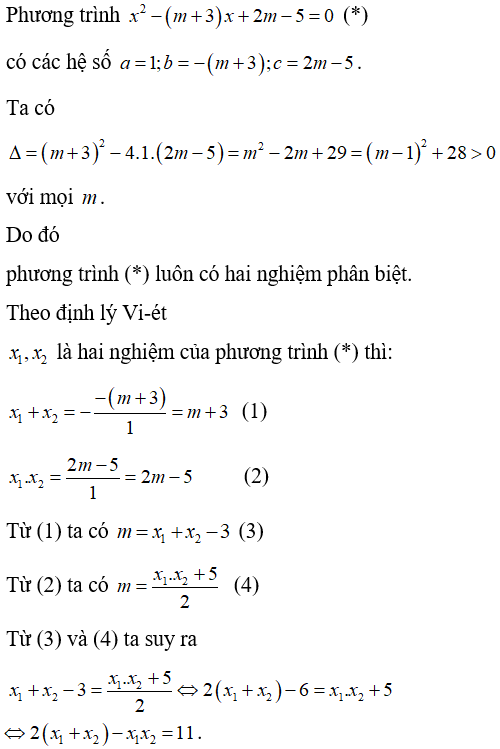
Ví dụ 4: Cho phương trình x2 – 2x – 8 = 0 có hai nghiệm x1 và x2. Phương trình bậc hai một ẩn có hai nghiệm là y1 = x1 – 3 và y2 = x2 – 3 là:

Lời giải
Chọn C

Bài 1: Tìm m để phương trình x2 – 3mx + 2m2 + 6 = 0 (m là tham số) có hai nghiệm là độ dài hai cạnh của hình chữ nhật có chu vi bằng 42 và diện tích bằng 104.

Lời giải:
Đáp án B

Bài 2: Hệ thức liên hệ giữa hai nghiệm của phương trình x2 – 2(m – 1)x – 2m + 1 = 0 không phụ thuộc vào m là:

Lời giải:
Đáp án D

Bài 3: Phương trình
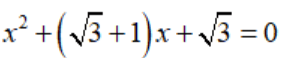
có hai nghiệm phân biệt x1; x2. Giá trị của biểu thức x12x2 + x1x22 bằng:

Lời giải:
Đáp án A
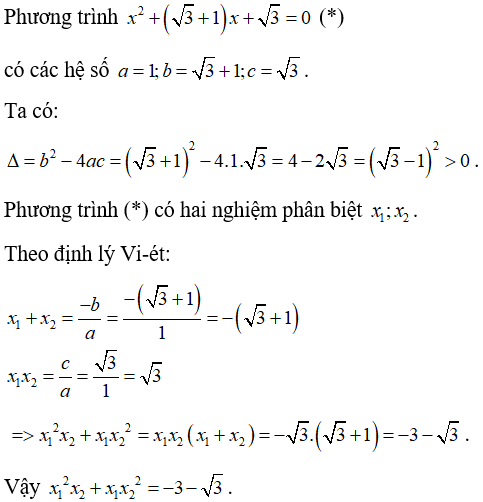
Bài 4: Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình x2 – 2x – 3 = 0. Giá trị của biểu thức S2 + 2P là:

Lời giải:
Đáp án B

Bài 5: Cho phương trình x2 – (m2 + 1)x + 3m2 – 8 = 0 (với m là tham số). Tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn x1 = 4x2 là:
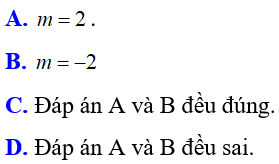
Lời giải:
Đáp án C
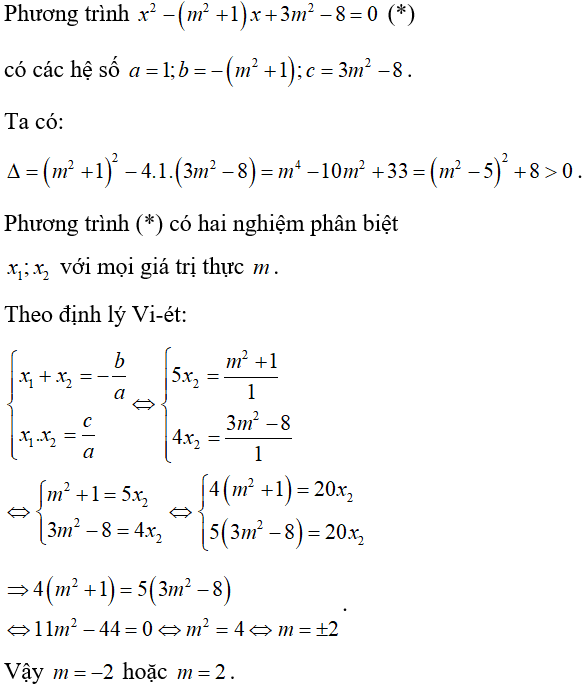
Bài 6: Phương trình nào sau đây có nghiệm bằng nghịch đảo các nghiệm của phương trình x2 + mx – 2 = 0?

Lời giải:
Đáp án B

Bài 7: Cho phương trình x2 – 2x – m2 = 0 có hai nghiệm x1 và x2. Phương trình bậc hai một ẩn có hai nghiệm là y1 = 2x1 – 1 và y2 = 2x2 – 1 là:
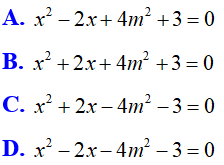
Lời giải:
Đáp án D
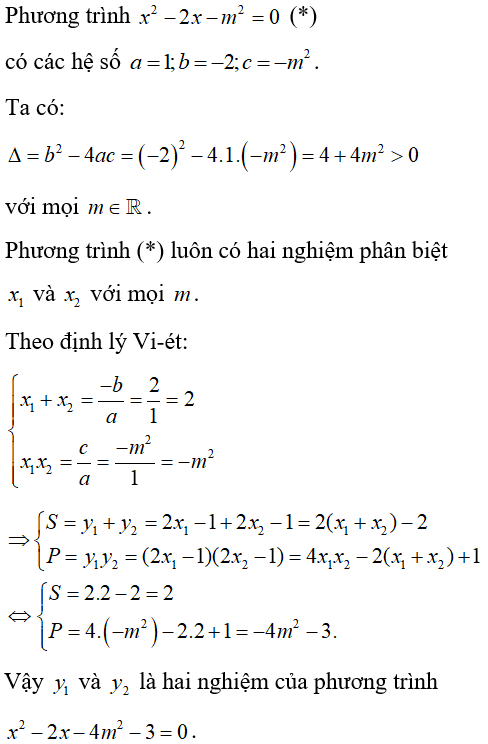
Bài 8: Cho phương trình bậc hai ẩn x , tham số m: mx2 – (2m + 3)x + m – 4 = 0. Với các giá trị của m để phương trình có hai nghiệm x1, x2, biểu thức liên hệ giữa hai nghiệm không phụ thuộc vào m là:
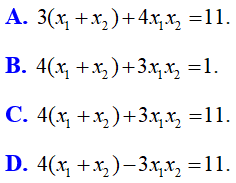
Lời giải:
Đáp án C
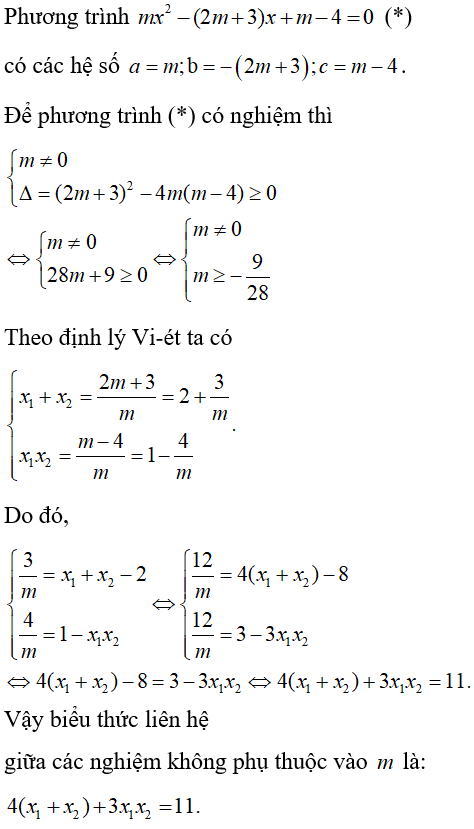
Bài 9: Tìm m để phương trình x2 + 3x + m – 1 = 0 có hai nghiệm x1, x2 thỏa mãn x1(x14 – 1) + x2(32x24 – 1) = 3

Lời giải:
Đáp án D
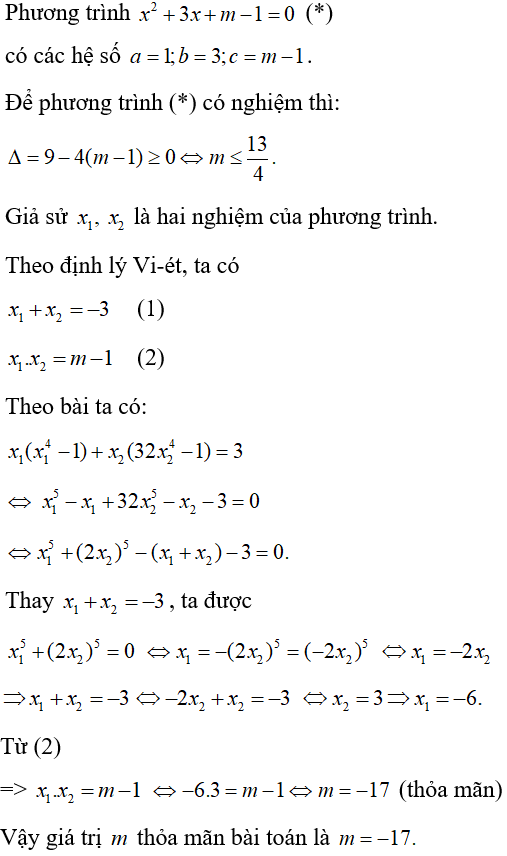
Bài 10: Cho phương trình x2 – 2(m – 2)x – 2m = 0. Giá trị của m để phương trình có hai nghiệm x1, x2 thỏa mãn x2 – x1 = x12 là:
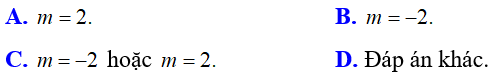
Lời giải:
Đáp án A
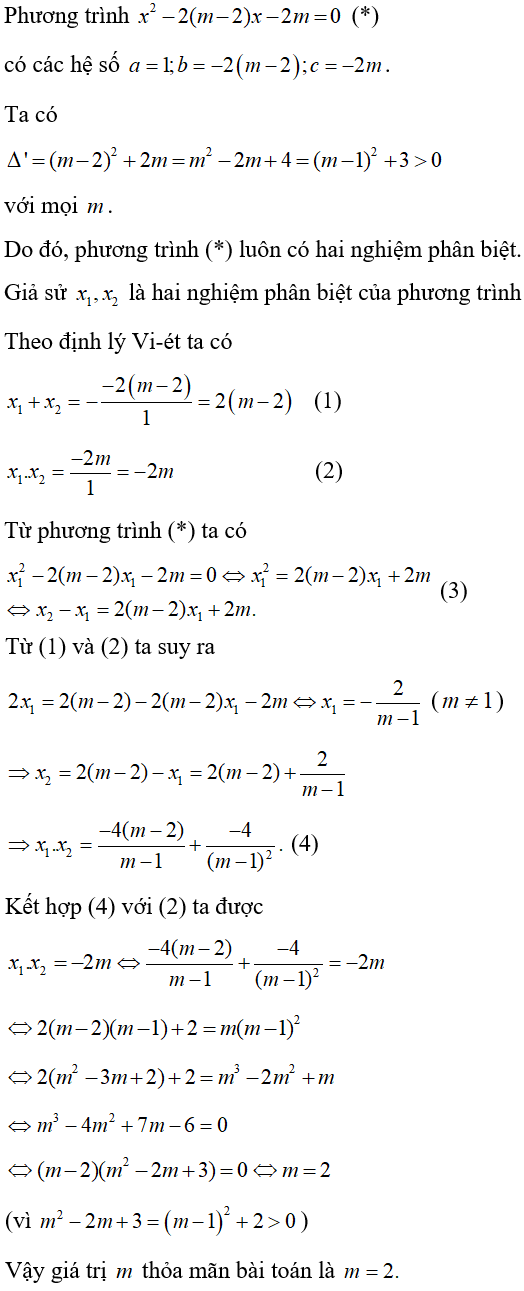
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

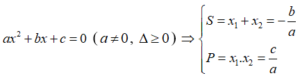

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn