Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm – Tổng hợp các dạng bài tập Toán 11 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 11.-Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm
Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm
Bài viết Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm.
Viết phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm
*Ý nghĩa hình học của đạo hàm:
Đạo hàm của hàm số y= f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M0(x0; f(x0) ).
Khi đó phương trình tiếp tuyến của (C) tại điểm M0 là:
y–y0=f’ (x0).(x–x0)
Bài toán 1. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) tại điểm M(x0; f(x0)).
– Tính đạo hàm của hàm số y= f(x)
⇒ f’( x0).
-Tiếp tuyến của đồ thị hàm số y= f(x) tại M( x0;y0) là:
y- y0= f’(x0) ( x- x0)
Bài toán 2. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) biết hoành độ tiếp điểm x= x0.
+ Tính y0= f(x0).
+ Tính đạo hàm của hàm số ⇒ f^’ (x0 )
⇒ phương trình tiếp tuyến: y- y0= f’(x0) ( x- x0)
Bài toán 3. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) biết tung độ tiếp điểm bằng y0.
+ Gọi M(x0; y0) là tiếp điểm
+ Giải phương trình f(x)= y0 ta tìm được các nghiệm x0.
+ Tính đạo hàm của hàm số ⇒ f'(x0)
⇒ Phương trình tiếp tuyến của đồ thị hàm số.
Ví dụ 1. Cho hàm số y= x3– 2x+ 1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M( 0;1 )
A. y= 2x+ 3 B. y= -2x + 1 C.y= 4x+1 D. y= – 4x+1
Hướng dẫn giải
+ Đạo hàm của hàm số đã cho là: y’= 3x2– 2
⇒ y'(0)= -2
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm M( 0;1) là:
y- 1= -2(x-0) hay y= -2x + 1
Chọn B.
Ví dụ 2. Cho hàm số y= x2 + 2x – 6. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là 1?
A. y= 2x+1 B. y= – 6x+ 1 C. y= 4x- 7 D. y= 3x-
Hướng dẫn giải
+ Ta có: y(1) = 12+ 2.1 – 6= -3
+ Đạo hàm của hàm số đã cho là: y’(x)= 2x+ 2
⇒ y’(1) = 2.1+ 2= 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x= 1 là:
y+ 3= 4( x- 1) hay y= 4x- 7
Chọn C.
Ví dụ 3. Cho hàm số y= x3 + 4x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2?
A. y= 4x+ 2 B. y = – 2x+ 1 C. y= 3x+ 1 D. y= 6x+ 1
Hướng dẫn giải
+ Xét phương trình: x3+ 4x+ 2= 2
⇔ x3+ 4x = 0 ⇔x= 0
+ Đạo hàm của hàm số đã cho là: y’ = 3x2 + 4
⇒ y’( 0) = 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2:
y- 2= 4( x – 0) hay y= 4x+ 2
Chọn A.
Ví dụ 4. Cho hàm số y= – x3 + 2x2+ 2x+1 có đồ thị (C). Gọi A là giao điểm của đồ thị (C) với trục tung. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm A?
A. y= – 2x+ 1 B. y= 3x- 2 C. y= 4x+ 1 D. y= 2x+ 1
Hướng dẫn giải
+ Do A là giao điểm của đồ thị (C) với trục tung nên tọa độ điểm A( 0; 1) .
+ Đạo hàm y’= – 3x2+ 4x + 2
⇒ y’( 0) = 2
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm A là:
y- 1= 2( x- 0) hay y= 2x+ 1
chọn D.
Ví dụ 5. Cho hàm số y= x2– 3x+ 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm của đồ thị hàm số với trục hoành ?
A. y= -x+ 1 và y= x – 2 B. y= x+ 1 và y= – x+ 3
C. y= – 2x + 1 và y= x- 2 D. Đáp án khác
Hướng dẫn giải
+ Giao điểm của đồ thị hàm số đã cho với trục hoành là nghiệm phương trình :
x2– 3x+2 = 0
Vậy đồ thị của hàm số đã cho cắt trục hoành tại hai điểm là A( 1; 0) và B( 2; 0).
+ Đạo hàm của hàm số đã cho: y’= 2x- 3
+ Tại điểm A( 1; 0) ta có: y’( 1)= – 1
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại A là:
y- 0= -1( x-1) hay y= – x+ 1
+ tại điểm B( 2; 0) ta có y’( 2)= 1
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại B là :
y- 0= 1( x- 2) hay y= x- 2
Vậy có hai tiếp tuyến thỏa mãn là: y= -x+ 1 và y= x- 2
Chọn A.
Ví dụ 6. Cho hai đường thẳng d1: 2x+ y- 3= 0 và d2: x+ y – 2= 0. Gọi A là giao điểm của hai đường thẳng đã cho. Cho hàm số y= x2+ 4x+ 1 có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A.
A. y= 3x- 5 B.y= 6x+ 1 C. y= 6x – 5 D. y= 2x+ 1
Hướng dẫn giải
+ Giao điểm của hai đường thẳng d1 và d2 là nghiệm hệ phương trình:
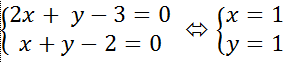
Vậy hai đường thẳng đã cho cắt nhau tại A( 1; 1).
+ Đạo hàm của hàm số đã cho là: y’= 2x+ 4
⇒ y’( 1) = 6.
⇒ Phương trình tiếp tuyến của đồ thị ( C) tại điểm A( 1; 1) là:
y-1= 6( x- 1) hay y= 6x- 5
Chọn C.
Ví dụ 7. Cho hàm số y =x4+ 2x2+ 1 có đồ thị ( C). Gọi d là tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ nguyên dương nhỏ nhất. Đường thẳng d song song với đường thẳng nào?
A. y= – 6x B. y= 8x C. y= – 10x D. y= 12x
Hướng dẫn giải
+ Đạo hàm của hàm số đã cho là: y’= 4x3+ 4x
+ Số nguyên dương nhỏ nhất là 1. Ta viết phương trình tiếp tuyến của đồ thi (C) tại điểm có hoành độ là 1.
+ ta có; y’(1)= 8 và y(1)=4
⇒ Phương trình tiếp tuyến của đồ thị hàm số ( C) tại điểm có hoành độ là 1 là:
y- 4= 8( x- 1) hay y= 8x- 4
⇒ Đường thẳng d song song với đường thẳng y= 8x
Chọn B.
Ví dụ 8.Phương trình tiếp tuyến của đồ thị hàm số y=( x- 1)2( x- 2) tại điểm có hoành độ x= 2 là
A. y= – 2x- 1 B. y= x+ 1 C. y= 3x+ 1 D. y= x- 2
Hướng dẫn giải
+Gọi M(x0 ; y0) là tọa độ tiếp điểm.
Từ x0=2 ⇒ y0= 0
+ Ta có : y= (x-1)2( x-2)= ( x2-2x+ 1) ( x- 2)
Hay y= x3– 4x2+ 5x- 2
⇒ Đạo hàm của hàm số đã cho là : y’= 3x2– 8x + 5
⇒ y’(2)= 1
Vậy phương trình tiếp tuyến cần tìm là :
y- 0= 1( x- 2) hay y= x- 2
chọn D.
Ví dụ 9. Cho hàm số y= (x-2)/(2x+1). Phương trình tiếp tuyến tại A( -1; 3) là
A. y= 5x+ 8 B. y= – 2x+3 C. y= 3x+ 7 D. Đáp án khác
Hướng dẫn giải
Đạo hàm của hàm số đã cho là;
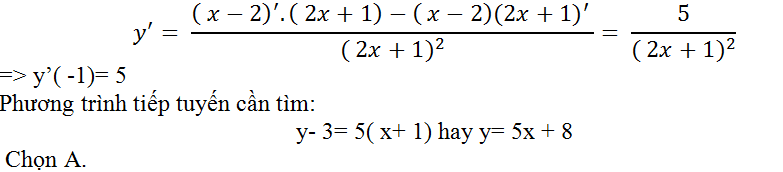
Ví dụ 10 .Cho hàm số y=2x+m+1/x-1 (C). Tìm m để tiếp tuyến của (C) tại điểm có hoành độ x0= 0 đi qua A(4; 3)

Hướng dẫn giải
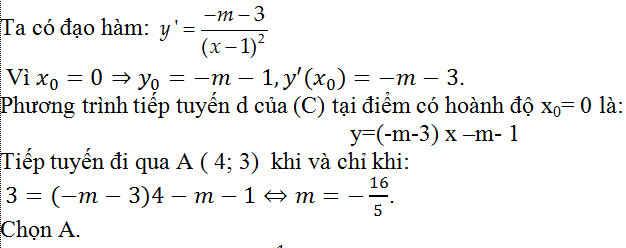
Ví dụ 11:Cho hàm số y=1/3 x3+x2-2 có đồ thị hàm sô (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y”=0 là
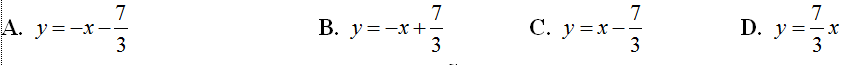
Hướng dẫn giải
Ta có y’=x2 +2x và y”=2x+2
Theo giả thiết x0 là nghiệm của phương trình
⇔2x+2=0⇔x0=-1
Và y’(-1)=-1
Phương trình tiếp tuyến tại điểm A(-1;-4/3)là: y= -1.(x+1)- 4/3
Hay y=-x-7/3
Chọn A.
Câu 1: Gọi (P) là đồ thị của hàm số y= 2x2+ 4x- 2. Phương trình tiếp tuyến của (P) tại điểm mà (P) cắt trục tung là:
A. y= 2x- 1 B. y= 3x+ 6 C. y= 4x- 2 D. y= 6x+ 3
Lời giải:
Ta có : (P) cắt trục tung tại điểm M( 0 ; -2)
Đạo hàm của hàm số đã cho : y’= 4x + 4
Hệ số góc tiếp tuyến : y’(0) = 4
Phương trình tiếp tuyến của đồ thị (P) tại M(0 ; -2) là
y+ 2= 4( x- 0) hay y= 4x – 2
chọn C.
Câu 2: Đồ thị (C) của hàm số y= (x2-2)/(x+2) cắt trục tung tại điểm A. Tiếp tuyến của (C) tại điểm A có phương trình là:
A. = 1/4 x+1 B. y= 1/2 x-1 C. y= -1/2 x-3 D. y= 2x- 1
Lời giải:
Ta có đồ thị ( C) cắt trục tung tại điểm A nên tọa độ A(0 ; -1)
Đạo hàm của hàm số đã cho là :
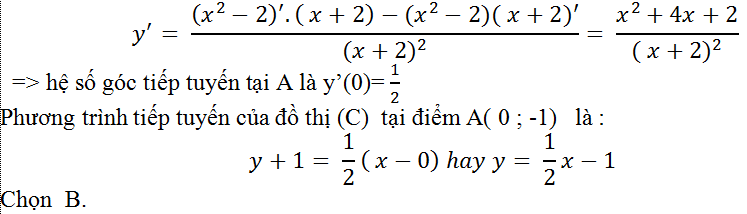
Câu 3: Cho hàm số y= (2-2x)/(x+1) có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:
A. y=2x+ 2 B. y= 4x- 3 C.y= -x+ 1 D. y= – 2x- 1
Lời giải:
Giao điểm của (H) với trục hoành là nghiệm hệ phương trình:
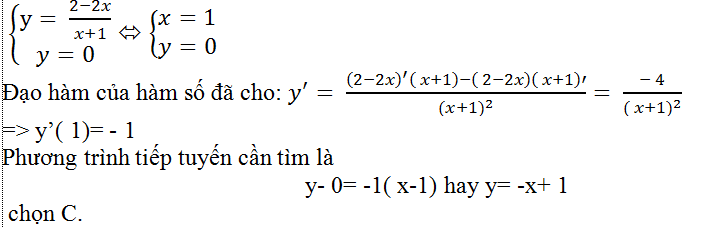
Câu 4: Gọi (C) là đồ thị hàm số y= x4 – 2x2+ 1. Có bao nhiêu tiếp tuyến của đồ thị (C) tại các giao điểm của (C) với hai trục toạ độ?
A.0 B. 1 C. 2 D. 3
Lời giải:
+ Giao điểm của đồ thị hàm số ( C) với trục hoành là nghiệm hệ phương trình:
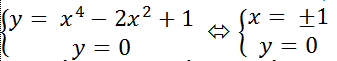
Vậy đồ thị hàm số ( C) cắt trục hoành tại hai điểm là A(1;0) và B( -1; 0). Tương ứng với hai điểm này ta viết được hai phương trình tiếp tuyến của đồ thị hàm số.
+ giao điểm của đồ thị hàm số (C) với trục tung là nghiệm hệ phương trình
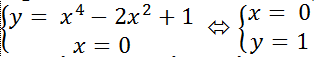
Vậy đồ thị hàm số (C) cắt trục tung tại một điểm là C(0; 1).
Vậy có ba tiếp tuyến thỏa mãn đầu bài.
Chọn C.
Câu 5: Lập phương trình tiếp tuyến của đồ thị (C): y= 2x3– 3x+ 1 tại giao điểm của (H) với đường thẳng d: y= – x+ 1
A. y= 3x- 2 và y= – 2x+ 1 B. y= – 3x+1 và y= 3x- 2
C. y=3x- 3 và y= – 2x+ 1 D. Đáp án khác
Lời giải:
+ Phương trình hoành độ giao điểm của đồ thị hàm số ( C) và đường thẳng d là:
2x3-3x + 1= – x+ 1
⇔2x3– 2x= 0 ⇔ 2x( x- 1) ( x+ 1) =0
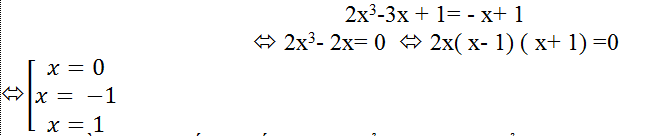
+ Vậy đồ thị hàm số (C) cắt đường thẳng d tại ba điểm là A(0; 1); B( – 1; 2) và C( 1; 0)
+ Đạo hàm của hàm số: y’= 6x2– 3
+ Tại điểm A( 0; 1) ta có y’(0) = – 3
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm A là;
y- 1 = -3( x- 0) hay y= – 3x+ 1
+ Tại điểm B( -1; 2) ta có: y’(-1) = 3
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm B là:
y- 2= 3( x+ 1) hay y= 3x + 5
+ tại điểm C( 1; 0) ta có y’(1)=3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm C là :
y-0= 3( x- 1) hay y= 3x – 3
chọn D.
Câu 6: Cho hàm số: y=x3-(m-1)x2+(3m+1)x+m-2. Tìm m để tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 đi qua điểm ( 2; -1).
A. m= 1 B. m= – 2 C. m= 3 D. m= 0
Lời giải:
Hàm số đã cho xác định với mọi x thuộc j .
Ta có đạo hàm: y’=3x2-2(m-1)x+3m+1
Với x=1 ⇒y(1)=3m+1 ⇒y'(1)=m+6
Phương trình tiếp tuyến tại điểm x=1 là:
Tiếp tuyến này đi qua A( 2; -1) nên có: -1=m+6+3m+1 ⇒m=-2
Vậy m = -2 là giá trị cần tìm.
Chọn B.
Câu 7: Gọi (C) là đồ thị của hàm số: y= (x-1)/(x-3). Gọi M là một điểm thuộc (C) và có khoảng cách đến trục hoành là 2. Viết phương trình tiếp tuyến của ( C) tại M
A. y= (- 1)/2x + 9/2 B. y= (- 9)/2 x+ 17/2
C. Cả A và B đúng D. Đáp án khác
Lời giải:
+ Do khoảng cách từ M đến trục hoành là 2 nên yM= 2 hoặc – 2
+ Nếu yM = 2; do điểm M thuộc đồ thị hàm số ( C) nên:
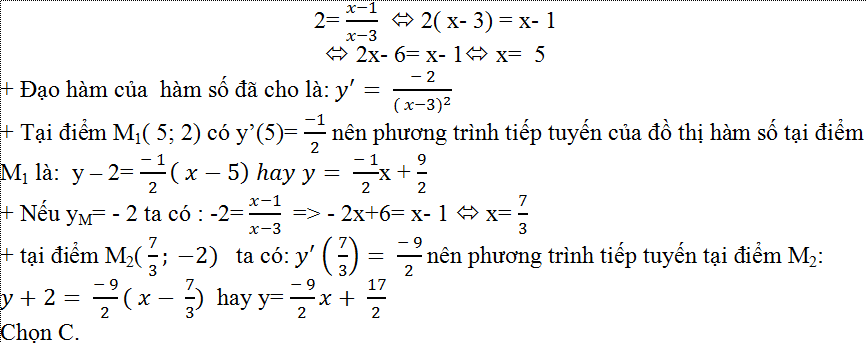
Câu 8: Cho hàm số y=x-2/x=+1. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp điểm M có tung độ bằng 4
A: y=9x+2 B: y=9x-16 C: y=9x+8 D: y=9x-2
Lời giải:
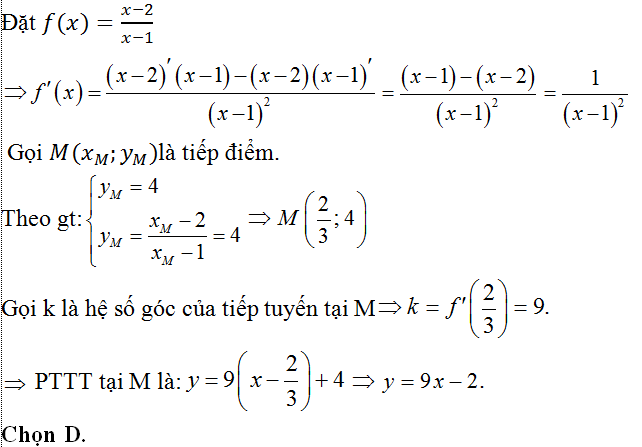
Câu 9: Cho hàm số y=x3+x2+x+1. Viết phương trình tiếp tuyến tại M thuộc đồ thị hàm số biết tung độ điểm M bằng
A: y=2x+1 B: y=x+1 C: y=x+2 D: y=x-1
Lời giải:
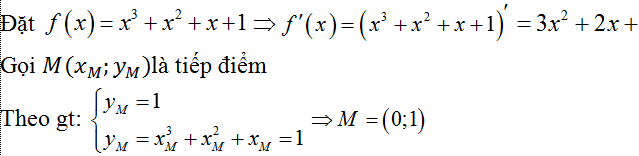
Gọi k là hệ số góc của tiếp tuyến tại M⇒ k=f’(0)=1
⇒phương trình tiếp tuyến tại M là:
Hay y=x+1
Chọn B.
Câu 10: Cho hàm số : y=√(1-x-x2 ) có đồ thị (C). Tìm phương trình tiếp tuyến với (C) tại điểm có hoành độ x0 =1/2 .
A: y+2x-1,5=0 B: 2x-y+1,5=0 C: -2x+y+1,5=0 D: 2x+y+1,5=0
Lời giải:
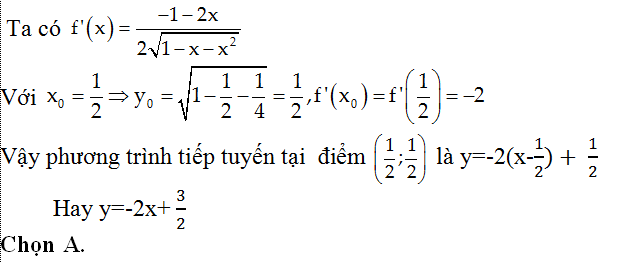
Bài 1. Cho hàm số y = x2 + 3x – 6. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là 2?
Bài 2. Cho hàm số y = x3 + 4x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 1?
Bài 3. Viết phương trình tiếp tuyến của đồ thị (C): y = -4x3 + 3x + 1 đi qua điểm A(-1; 2)
Bài 4. Cho hai đường thẳng d1: 2x+ y – 3 = 0 và d2: x+ y – 2 = 0. Gọi A là giao điểm của hai đường thẳng đã cho. Cho hàm số y = x2 + 4x + 2 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A.
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số y = (x – 1)2(x – 2) tại điểm có hoành độ x = 5.

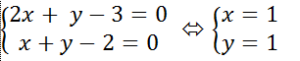
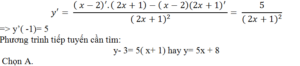

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn