Cách xét dấu các nghiệm của phương trình bậc hai lớp 9 (cực hay, có đáp án) – Chuyên đề Toán 9 tổng hợp phương pháp giải các dạng bài tập Toán 9 hay, chi tiết giúp bạn học tốt Toán 9.-Cách xét dấu các nghiệm của phương trình bậc hai lớp 9 (cực hay, có đáp án)
Cách xét dấu các nghiệm của phương trình bậc hai lớp 9 (cực hay, có đáp án)
Bài viết Cách xét dấu các nghiệm của phương trình bậc hai lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách xét dấu các nghiệm của phương trình bậc hai.
Cách xét dấu các nghiệm của phương trình bậc hai lớp 9 (cực hay, có đáp án)
Cho phương trình ax2 + bx + c = 0 (a ≠ 0)
Bước 1: Xác định hệ số a; b; c.
Bước 2: Tính Δ = b2 – 4ac (hoặc Δ’ = b’2 – ac) để kiểm tra phương trình có nghiệm hay không.
Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ’ ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình: 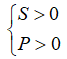 .
.
+) Phương trình có hai nghiệm cùng dấu: P > 0.
+) Phương trình có hai nghiệm dương: 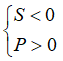 .
.
+) Phương trình có hai nghiệm âm:  .
.
+) Phương trình có hai nghiệm trái dấu: P < 0.
Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0. hoặc a.c < 0.
Bước 4: Kết luận.
Ví dụ 1: Cho phương trình x2 – 2x + 1 – m2 = 0 với m là tham số. Khẳng định nào sau đây là đúng?

Lời giải
Chọn D

Ví dụ 2: Giá trị nguyên nhỏ nhất của tham số m để phương trình x2 – 2(m + 7)x + m2 – 4 = 0 có hai nghiệm trái dấu là:

Lời giải
Chọn C

Ví dụ 3: Phương trình 2x2 + (2m – 1)x + m – 1 = 0 có hai nghiệm bằng nhau về giá trị tuyệt đối nhưng trái dấu nhau khi:

Lời giải
Chọn C
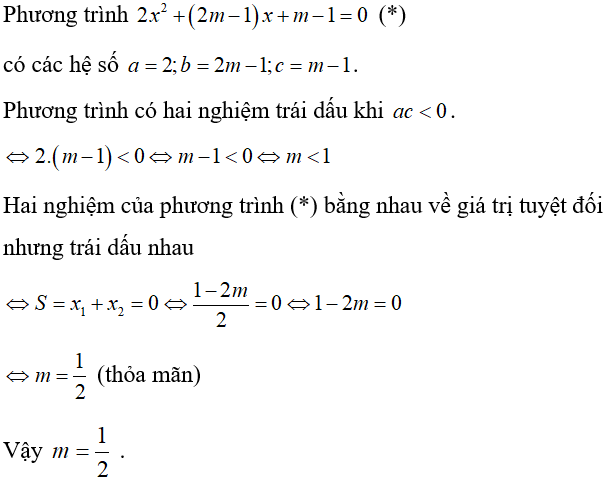
Bài 1: Cho phương trình bậc hai (m – 1)x2 – 2mx + m + 2 = 0 (với m là tham số). Chọn khẳng định sai trong các khẳng định sau:

Lời giải:
Đáp án A
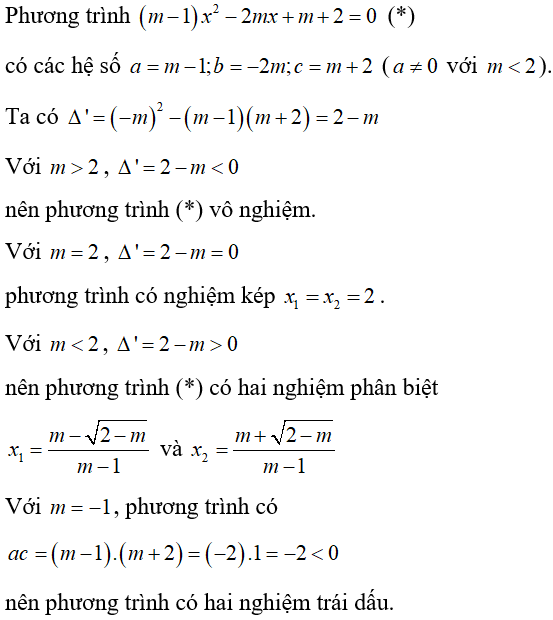
Bài 2: Phương trình nào sau đây luôn có hai nghiệm trái dấu với mọi tham số m?
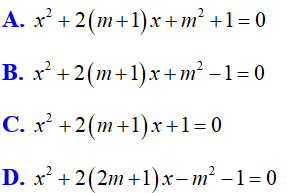
Lời giải:
Đáp án D

Bài 3: Chọn khẳng định đúng trong các khẳng định sau:
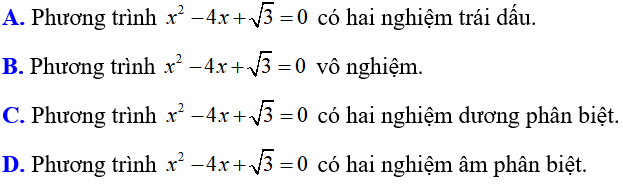
Lời giải:
Đáp án C

Bài 4: Cho các phương trình:

Số phương trình có hai nghiệm âm phân biệt là:

Lời giải:
Đáp án B

Bài 5: Giá trị của m để phương trình 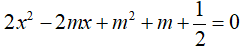 có nghiệm âm là:
có nghiệm âm là:
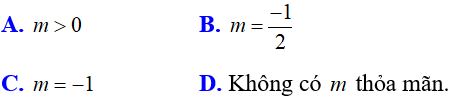
Lời giải:
Đáp án C

Bài 6: Biết rằng phương trình 3x2 – mx – m2 + 2m – 4 = 0 luôn có nghiệm với mọi tham số m. Chọn khẳng định đúng.

Lời giải:
Đáp án D
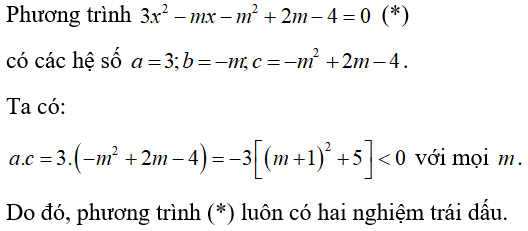
Bài 7: Tìm m để phương trình x2 – (3m – 1)x + 10m = 0 có hai nghiệm x1, x2 là độ dài hai cạnh của tam giác vuông có cạnh huyền là 13.
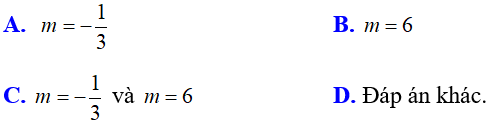
Lời giải:
Đáp án B
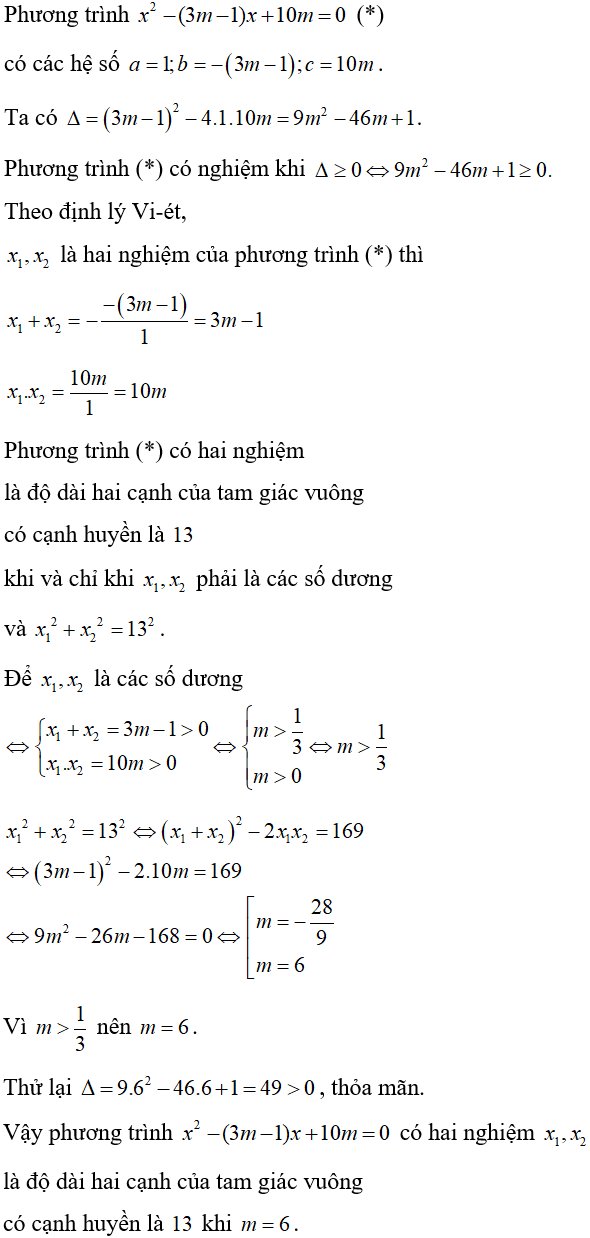
Bài 8: Cho phương trình x2 + (3m – 1)x + m2 = 0 (với m là tham số). Giá trị nguyên nhỏ nhất của m để phương trình có hai nghiệm âm phân biệt là:

Lời giải:
Đáp án A
Bài 9: Tìm m để phương trình x2 + 3mx + 2m2 + 6 = 0 (m là tham số) có hai nghiệm là độ dài hai cạnh của hình chữ nhật có diện tích bằng 104.

Lời giải:
Đáp án A

Bài 10: Phương trình nào sau đây luôn có hai nghiệm âm với mọi tham số m?
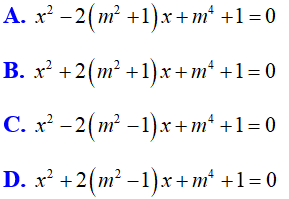
Lời giải:
Đáp án B


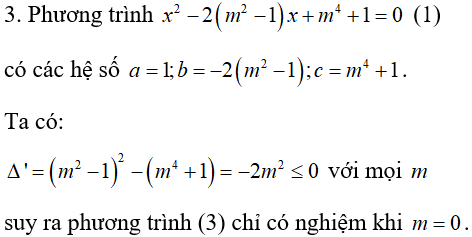
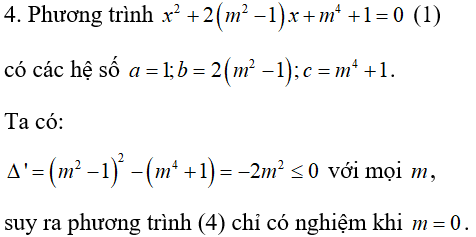
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

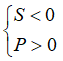


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn