Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay | Chuyên đề Toán 9 – Bộ chuyên đề Toán lớp 9: Đại số và Hình học gồm các dạng bài tập cơ bản và nâng cao có lời giải chi tiết được biên soạn theo chương trình sgk Toán 9 giúp bạn học tốt môn Toán lớp 9.-Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay
Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay
Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp lớp 9 với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh
ôn tập, biết cách làm bài tập phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp.
Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay
Bước 1: Tìm đkxđ.
Bước 2: Nhẩm nghiệm (thường là nghiệm nguyên). Giả sử phương trình có nghiệm x = a
Bước 3: Tách, thêm bớt rồi nhân liên hợp sao cho xuất hiện nhân tử chung (x – a).
Các biểu thức liên hợp thường dùng:
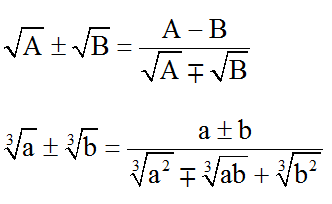
Bước 4. Chứng minh biểu thức còn lại luôn âm hoặc dương
Bước 5. Đối chiếu điều kiện, kết luận nghiệm.
Ví dụ 1: Giải phương trình: 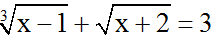
Hướng dẫn giải:
Phân tích: Để ý thấy x = 2 là nghiệm của phương trình, do đó ta có thể liên hợp 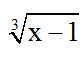 và 1;
và 1; 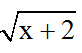 và 2.
và 2.
Đkxđ: x ≥ -2 .
Ta có:
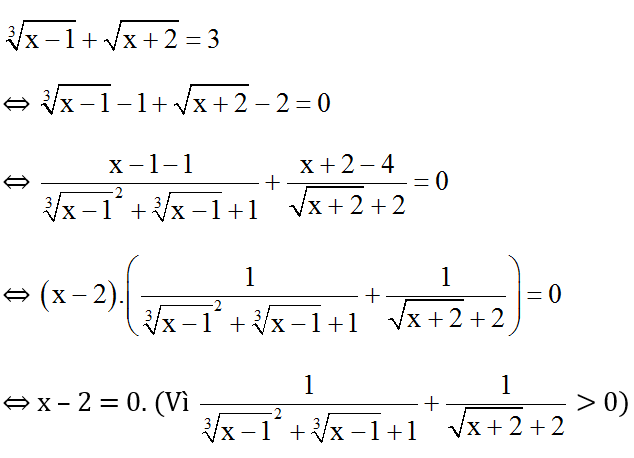
⇔ x = 2 (t.m đkxđ)
Vậy phương trình có nghiệm x = 2.
Ví dụ 2: Giải phương trình: 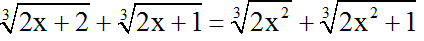
Hướng dẫn giải:
Đkxđ: ∀ x ∈ R
Ta có:
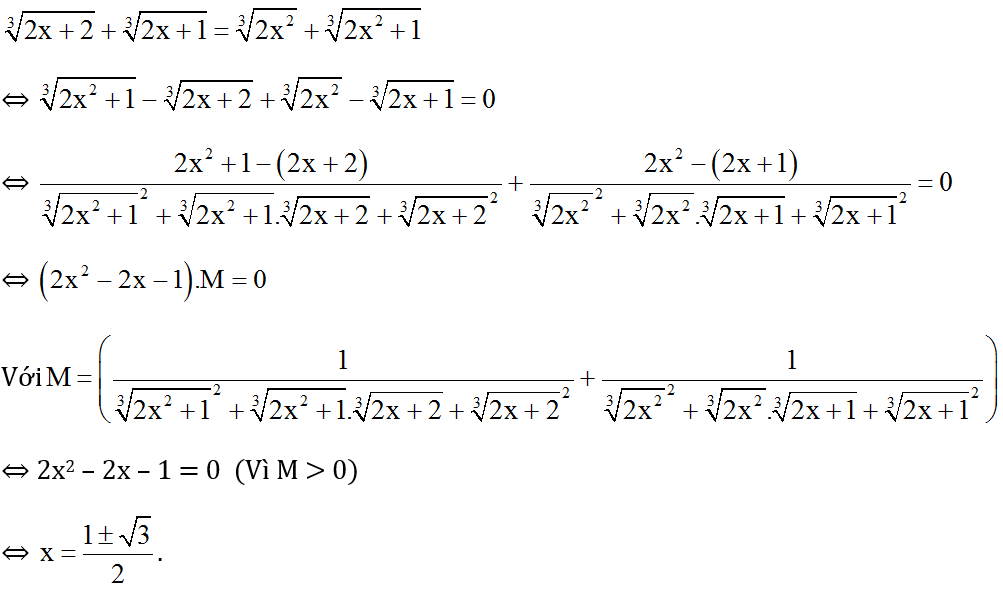
Vậy phương trình có hai nghiệm 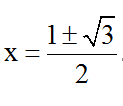 .
.
Ví dụ 3: Giải phương trình 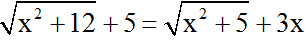
Hướng dẫn giải:
Gợi ý: Nhẩm được phương trình có nghiệm x = 2 nên ta tách các biểu thức để liên hợp sao cho xuất hiện nhân tử (x – 2).
Đkxđ: ∀ x ∈ R
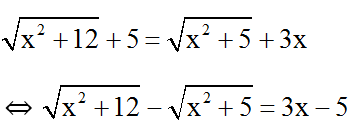
Vì 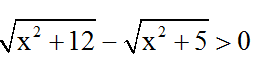 nên phương trình có nghiệm ⇔ 3x – 5 > 0 ⇔ x > 5/3 .
nên phương trình có nghiệm ⇔ 3x – 5 > 0 ⇔ x > 5/3 .
Khi đó:
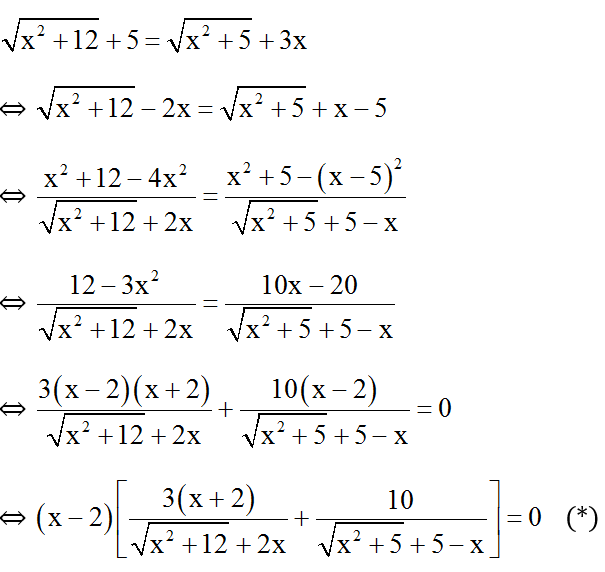
Với x > 5/3 > 0 thì 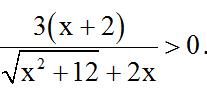 .
.
Lại có 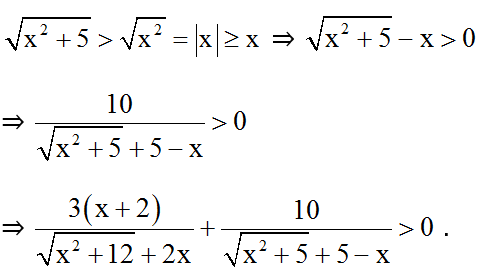
(*) ⇔ x – 2 = 0 ⇔ x = 2.
Vậy phương trình có nghiệm x = 2.
Bài 1: Biểu thức liên hợp của 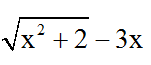 là:
là:
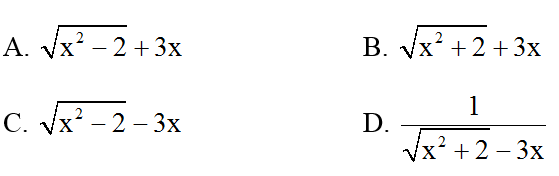
Đáp án: B
Bài 2: Biểu thức liên hợp của 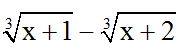 là:
là:
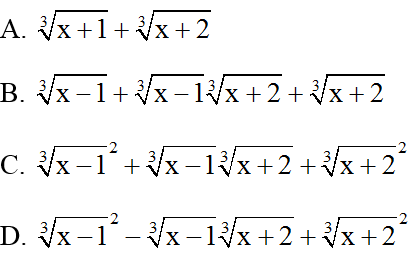
Đáp án: C
Bài 3: Biểu thức nào dưới đây bằng với biểu thức 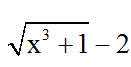
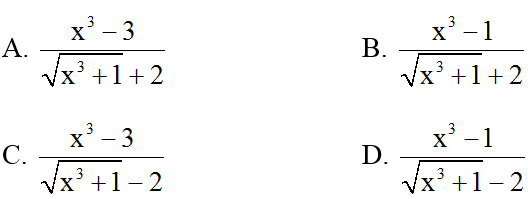
Đáp án: A
Bài 4: Biểu thức nào dưới đây bằng với biểu thức 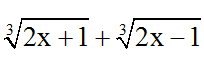
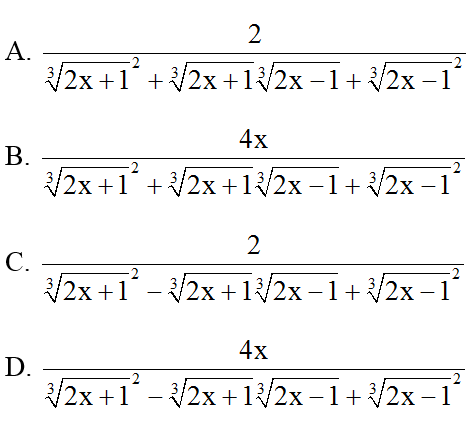
Đáp án: D
Bài 5: Nghiệm của phương trình 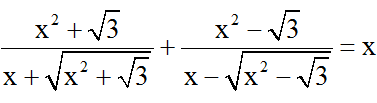 có nghiệm là:
có nghiệm là:
A. x = √2 B. x = -√2
C. x = √3 D. x = -√3
Đáp án: A
Bài 6: Giải phương trình 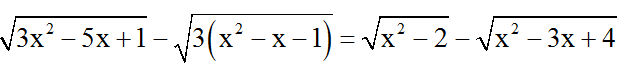
Hướng dẫn giải:
Đkxđ: 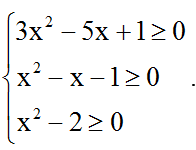
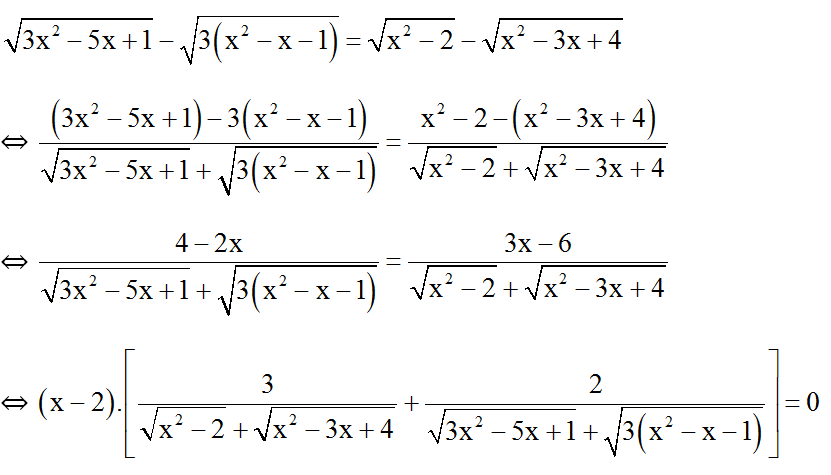
⇔ x – 2 = 0 (Vì biểu thức trong […] luôn dương)
⇔ x = 2 (t.m đkxđ).
Vậy phương trình có nghiệm x = 2.
Bài 7: Giải phương trình 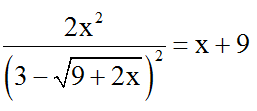
Hướng dẫn giải:
Đkxđ: x ≥ -9/2; x ≠ 0 .
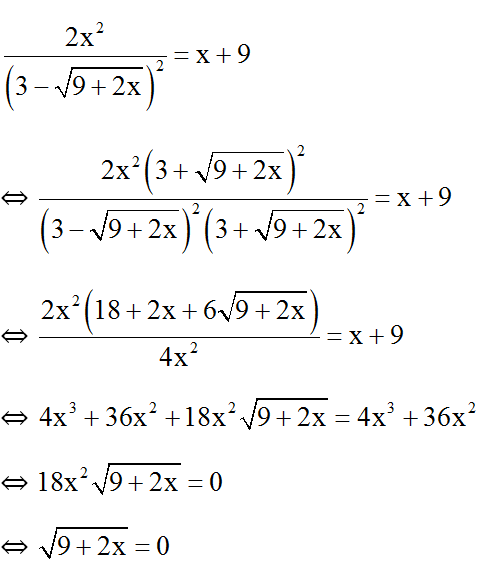
⇔ x = -9/2 (t.m đkxđ).
Vậy phương trình có nghiệm x = -9/2 .
Bài 8: Giải phương trình 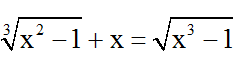
Hướng dẫn giải:
Đkxđ: x ≥ 1.
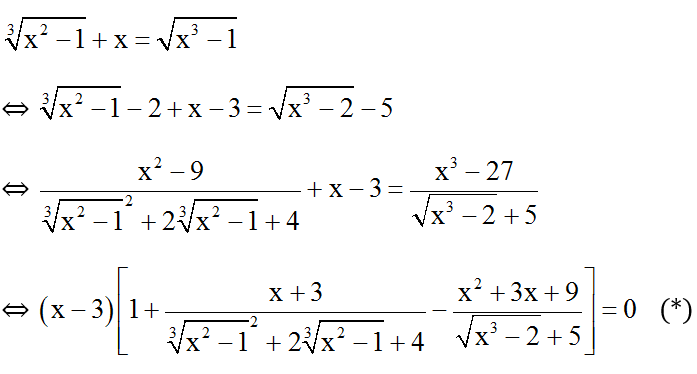
Ta chứng minh được:
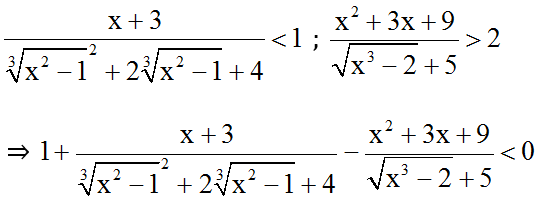
Khi đó (*) ⇔ x – 3 = 0 ⇔ x = 3 (t.m đk xđ).
Vậy phương trình có nghiệm x = 3.
Bài 9: Giải phương trình: 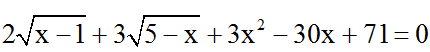
Hướng dẫn giải:
Đkxđ: 1 ≤ x ≤ 5 .
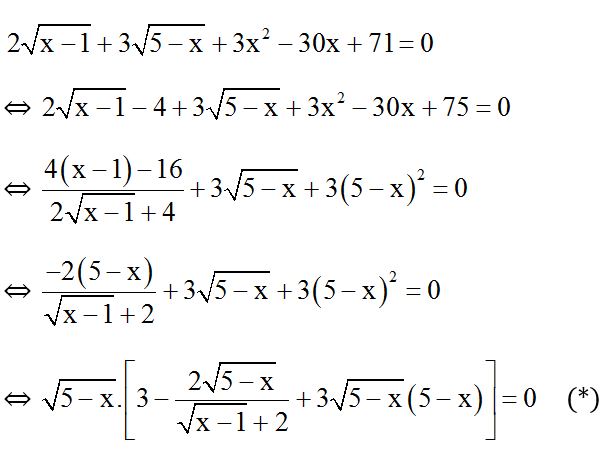
Ta thấy: 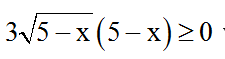 với 1 ≤ x ≤ 5 .
với 1 ≤ x ≤ 5 .
Ta chứng minh 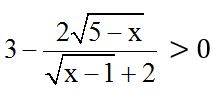
Thật vậy: Với 1 ≤ x ≤ x thì: 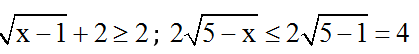
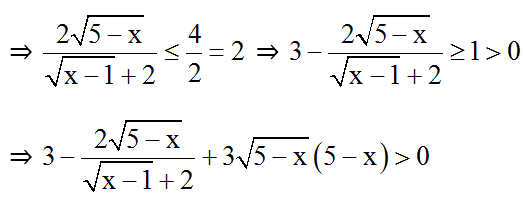
(*) ⇔ 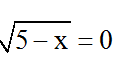 ⇔ x = 5 (t.m đkxđ).
⇔ x = 5 (t.m đkxđ).
Vậy phương trình có nghiệm x = 5.
Bài 10: Giải phương trình: 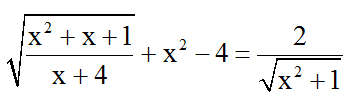
Hướng dẫn giải:
Đkxđ: x > -4.
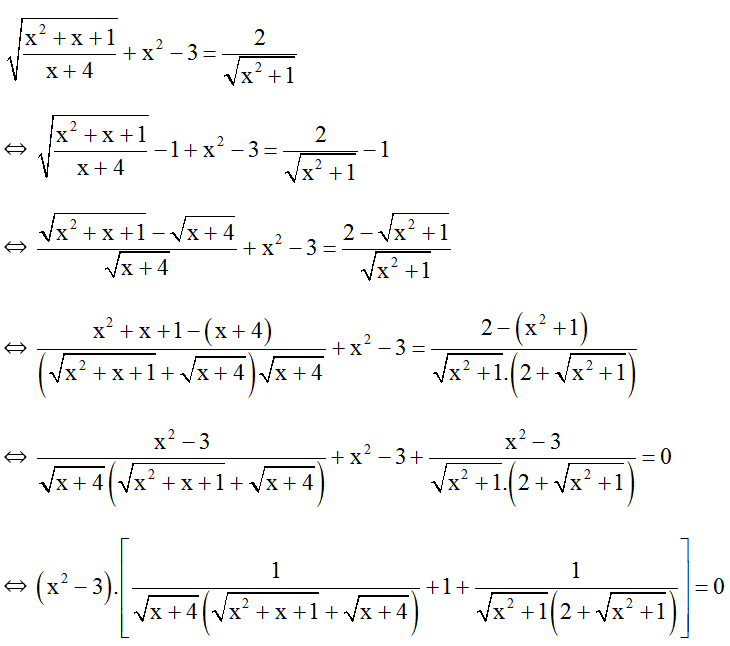
⇔ x2 – 3 = 0(Vì biểu thức trong [ ] luôn dương)
⇔ x2 = 3
⇔ x = ±√3(t.m đkxđ).
Vậy phương trình có hai nghiệm x = ±√3 .
Bài 1. Giải phương trình
a) x-2+4-x=2×2-5x-3;
b) 4x+3+19-3x=x2+2x+9;
c) 8x+1-46-10x=-x3+5×2-12x+17;
d) 2x+5-6-x+2×2+x-11=0.
Bài 2. Hãy tìm biểu thức liên hợp của biểu thức 3x-8-x+1=2x-115.
Bài 3. Cho phương trình x23+2×3-(x-4)x-7-3x+28=0. Tìm nghiệm của phương trình?
Bài 4. Số nghiệm của các phương trình.
a) 5×3-1+2x-13+x-4=0;
b) x2-13+x=x3-2;
c) x3+15+2=x3+8+3x.
Bài 5. Giải phương trình
a) x+3x=x2+72(x+1);
b) x3+5×2+4x+2×2+2x+3=x2+x+2.
Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:
Mục lục các Chuyên đề Toán lớp 9:

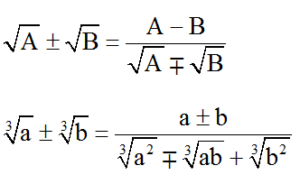

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn