Lý thuyết Tin 10 Kết nối tri thức Bài 4: Hệ nhị phân và dữ liệu số nguyên

Với tóm tắt lý thuyết Tin học lớp 10 Bài 4: Hệ nhị phân và dữ liệu số nguyên sách Kết nối tri thức hay nhất, ngắn gọn
sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Tin 10.

Lý thuyết Tin 10 Kết nối tri thức Bài 4: Hệ nhị phân và dữ liệu số nguyên

1. Hệ nhị phân và biêu diễn số nguyên

a) Hệ nhị phân

– Chỉ dùng hai số là 0 và 1, các chữ số 0 và 1 gọi là các chữ số nhị phân.

– Mỗi số có thể biểu diễn bởi một dãy các chữ số nhị phân.

– Trong biểu diễn số nhị phân, một chữ số ở một hàng có giá trị gấp 2 lần chính chữ số đó ở hàng liền kề bên phải. Chữ số 1 ở vị trí k kể từ phải sang trái là 2k−1 .

Ví dụ: Số 19 biểu diễn lũy thừa: 1×24+0×23+0×22+1×21+1×20 Trong hệ nhị phân số 19 biểu diễn là 10011.

Khi cần phân biệt số được biểu diễn trong hệ đếm, sử dụng cơ số làm chỉ số dưới 1910 hay 100112 .

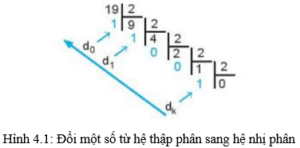
b) Đổi biểu diễn số nguyên dương từ hệ thập phân sang hệ nhị phân

Giả sử đổi số tự nhiên N trong hệ thập phân sang nhị phân dạng dkdk−1…d1,d0 có giá trị bằng 0 hoặc 1 sao cho N=dk×2k+dk−1×2k−1+…+d1×2+d0

Để tìm các số dk,dk−1,…d1,d0 , người ta chia liên tiếp N cho 2 để tìm số dư

Ví dụ: Chuyển đổi số 19 sang hệ nhị phân

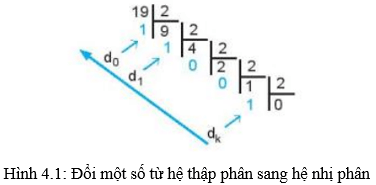
– Việc đổi số nhị phân dạng dk,dk−1,…d1,d0 sang số thập phân thực chất là tính tổng dk×2k+dk−1×2k−1+…+d1×2+d0 .

Ví dụ: 11012=1×23+1×22+0×21+1×20=13

c) Biểu diễn số nguyên trong máy tính

– Có hai phương pháp biểu diễn số trong máy tính là dấu phẩy tĩnh và dấu phẩy động (được dùng khi tính toán các số quá lớn, quá nhỏ hoặc không nguyên).

– Biểu diễn số nguyên không dấu chính là thể hiện của số trong hệ đếm cơ số 2.

Ví dụ: Số 19 trong hệ nhị phân là 10011 chỉ cần một byte với ba bit 0 bổ sung thêm bên trái cho đủ 8 bit.

– Với số nguyên có dấu, một số cách mã hóa khác nhau như mã thuận, mã đảo – còn gọi là mã bù 1 và mã bù 2.

+ Mã hóa này dành ra một bit bên trái để mã hóa dấu, dấu + mã hóa bởi bit có giá trị là 0, dấu – được mã hóa bởi bit có giá trị là 1.

+ Ví dụ: Nếu biểu diễn số trong một byte, tách ra một bit dấu, số +1910 trong mã thuận sẽ có mã là 00010011, trong khi đó −1910 sẽ có mã là 10010011.

2. Các phép tính số học trong hệ nhị phân

a) Bảng cộng và nhân trong hệ nhị phân

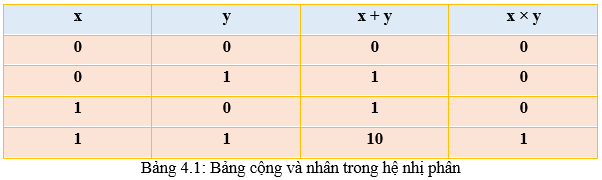
– Cộng và nhân trong hệ nhị phân tương tự trong hệ thập phân

Lưu ý: 1 + 1 = 10.

b) Cộng hai số nguyên không dấu

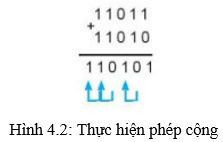
– Phép cộng được thực hiện tương tự trong hệ thập phân, thực hiện từ phải sang trái.

– Khi phép cộng hai bit có kết quả là 10 thì ghi 0 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng bên trái.

Ví dụ: Minh họa phép cộng hai số nhị phân 11011 và 11010

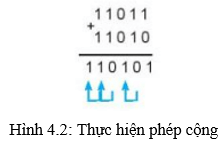
c) Nhân hai số nhị phân

– Phép nhân trong hệ nhị phân cũng thực hiện như trong hệ thập phân.

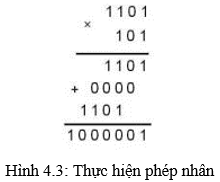
– Có thể coi tính toán số học trong máy tính là ứng dụng của hệ nhị phân.

Xem thêm tóm tắt lý thuyết Tin học lớp 10 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 10 hay khác:

---