Tìm m để hàm bậc ba có 2 điểm cực trị (cực hay, có lời giải) – Tổng hợp các dạng bài tập Toán 12 với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 12.-Tìm m để hàm bậc ba có 2 điểm cực trị (cực hay, có lời giải)
Tìm m để hàm bậc ba có 2 điểm cực trị (cực hay, có lời giải)
Bài viết Tìm m để hàm bậc ba có 2 điểm cực trị với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Tìm m để hàm bậc ba có 2 điểm cực trị.
Tìm m để hàm bậc ba có 2 điểm cực trị (cực hay, có lời giải)
Bài giảng: Các dạng bài tìm cực trị của hàm số – Cô Nguyễn Phương Anh (Giáo viên Meraki Center)
Xét hàm số y = ax3 + bx2 + cx + d, (a ≠ 0)
Khi đó y’ = 3ax2 + 2bx + c; y’ = 0 ⇔ 3ax2 + 2bx + c = 0
Hàm số có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
⇔ Δ’ > 0 ⇔ b2 – 3ac > 0
Ví dụ 1: Số giá trị nguyên của tham số m ∈ [-10;10] để hàm số 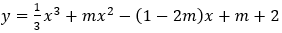 có cực đại, cực tiểu là:
có cực đại, cực tiểu là:
A. 20
B. 21
C. 10
D. 9
Lời giải
Chọn A
Ta có y’ = x2 + 2mx – (1 – 2m); y’ = 0 ⇔ x2 + 2mx – (1 – 2m) = 0
Hàm số đã cho có cực đại và cực tiểu ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
⇔ Δ’ > 0 ⇔ m2 + (1 – 2m) > 0 ⇔ (m – 1)2 > 0 ⇔ m ≠ 1
Kết hợp m nguyên và m ∈ [-10;10] thì có 20 giá trị của m thỏa mãn.
Ví dụ 2: Với giá trị nào của m thì hàm số y = x3 – 3x2 + 3(1 – m2)x + 1 có 2 điểm cực trị.
A. m ≠ 1
B. m ∈ R
C. m ≠ 0
D. Không tồn tại m
Lời giải
Chọn C
Ta có y’ = 3x2-6x + 3(1 – m2); y’ = 0 ⇔ x2-2x + 1 – m2 = 0
Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
⇔ Δ’ > 0 ⇔ 1 – (1 – m2)>0 ⇔ m2>0 ⇔ m ≠ 0
Ví dụ 3: Cho hàm số y = -2x3 + (2m – 1)x2 – (m2 – 1)x – 2. Số giá trị nguyên của m để hàm số đã cho có hai điểm cực trị là:
A. 3
B. 5
C. 6
D. 8
Lời giải
Chọn B
Ta có y’ = -6x2 + 2(2m – 1)x – (m2 – 1)
Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
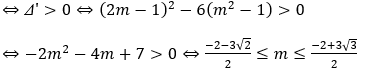
Do m nguyên nên m ∈ {-3;-2;-1;0;1}
Vậy có tất cả 5 giá trị nguyên của m thỏa mãn
Ví dụ 4: Tìm tất cả các giá trị của m để hàm số 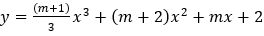 có 2 điểm cực trị.
có 2 điểm cực trị.
Lời giải
Có y’ = (m + 1)x2 + 2(m + 2)x + m
Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
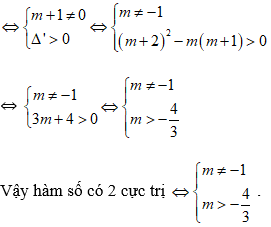
Bài 1. Cho hàm số y = -2x3 + (2m – 1)x2 – (m2 – 1)x – 2. Tìm số giá trị nguyên của m để hàm số đã cho có hai điểm cực trị.
Bài 2. Tìm tất cả các giá trị của m để hàm số y=m+13×3+m+2×2+mx+2 có 2 điểm cực trị.
Bài 3. Với giá trị nào của m thì hàm số y = x3 – 3x2 + 3(1 – m2)x + 1 có 2 cực trị?
Bài 4. Cho hàm số y = (m + 2)x3 + 3x2 + mx – 9. Tìm m để hàm số có 2 cực trị.
Bài 5. Cho hàm số bậc ba sau: y = x3 – 3mx + 1. Tìm m để hàm số đã cho có 2 cực trị.
Bài 6. Tìm tất cả các giá trị của tham số m để hàm số y = x3 – 3mx2 + 6mx + m có hai điểm cực trị.
Bài 7. Tìm m để hàm số y =13x3 – mx2 + (2m – 1)x + 2 có 2 điểm cực trị dương.
Bài 8. Tìm m để đồ thị hàm số y = x3 − 3mx2 + 2 có hai điểm cực trị.
Bài 9. Cho hàm số y = 13x3 − (2m + 3)x22 + (m2 + 3m)x – m + 1. Tìm m để hàm số có 2 cực trị.
Bài 10. Cho hàm số y = 23x3 + (m − 1)x2 − 4m(3m − 1)x + 7. Tìm m để hàm số có cực đại, cực tiểu.
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:

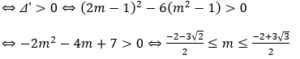

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn