Hiệu hai bình phương. Bình phương của một tổng hay một hiệu (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Hiệu hai bình phương. Bình phương của một tổng hay một hiệu (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

1. Hằng đẳng thức

Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.

Ví dụ 1:

a) Các đẳng thức thường gặp:

a + b = b + a;                c.d = d.c;             a(b – c) = a.b – a.c

là những hằng đẳng thức.

b) Đẳng thức a + 1 = 3a – 1 không phải là hằng đẳng thức vì khi ta thay a = 2 thì hai vế của đẳng thức không bằng nhau.

2. Hiệu hai bình phương

+ Với hai số a,b bất kì, thực hiện phép tính:

(a + b).(a – b) = a.a – a.b + b.a – b.b = a² – b²

+ Trong trường hợp A, B là những biểu thức tùy ý, ta cũng có:

A² – B² = (A – B)(A + B).

Ví dụ 2:

+ Tính nhanh 99² – 1.

Ta có: 99² – 1 = 99² – 1² = (99 + 1)(99 – 1) = 100 . 98 = 9 800.

+ Viết x² – 4 dưới dạng tích.

Ta có: x² – 4 = x² – 2² = (x + 2)(x – 2).

3. Bình phương của một tổng

+ Với hai số a, b bất kì, thực hiện phép tính:

(a + b)(a + b) = a.a + a.b + b.a + b.b = a² + 2ab + b²

Vậy (a + b)(a + b) = (a + b)² = a² + 2ab + b².

+ Trong trường hợp A, B là những biểu thức tùy ý, ta cũng có:

(A + B)² = A² + 2AB + B².

Ví dụ 3:

+ Tính nhanh 101².

101² = (100 + 1)² = 100² + 2.100.1 + 1²

        = 10 000 + 200 + 1 = 10 201.

+ Khai triển (x + 3y)²

(x + 3y)² = x² + 2.x.3y + (3y)² = x² + 6xy + 9y².

+ Viết biểu thức 9x² + 6x + 1 dưới dạng bình phương của một tổng.

9x² + 6x + 1 = (3x)² + 2.3x.1 + 1² = (3x + 1)².

4. Bình phương của một hiệu

+ Với hai số a, b bất kì ta viết

(a – b)² = [a + (–b)]² = a² + 2.a.(–b) + (–b)² = a² – 2ab + b².

+ Trong trường hợp A, B là hai biểu thức tùy ý ta có:

(A – B)² = A² – 2AB + B².

Ví dụ 4:

+ Khai triển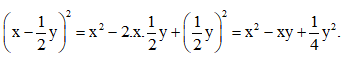

+ Tính nhanh 99² = (100 – 1)² = 100² – 2.100.1 + 1² = 10 000 – 200 + 1 = 9 801.

Bài tập Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Bài 1. Những đẳng thức nào sau đây là hằng đẳng thức?

a) 2x + 1 = x + 5;                                       

b) x(x + 1) =x² + x;

c) 4a(a – 1) = 4a² – 4a;                               

d) 2a + b = 2b + a.

Hướng dẫn giải

a) Đẳng thức 2x + 1 = x + 5 không là hằng đẳng thức vì khi ta thay x = 2 thì hai vế của đẳng thức không bằng nhau.

b) Đẳng thức x(x + 1) =x² + x là hằng đẳng thức.

c) Đẳng thức 4a(a – 1) = 4a² – 4a là hằng đẳng thức.

d) Đẳng thức 2a + b = 2b + a không là hằng đẳng thức vì khi ta thay a = 1, b = 5 thì hai vế của đẳng thức không bằng nhau.

Bài 2. Thay dấu ? bằng biểu thức thích hợp.

a) (2x – y)(2x + y) = ? – y²;

b) (x + 5y)(x – 5y) = x² – ? y²;

c) x² + ? xy + 4y² = (x + 2y)²;

d) (? + 3)² = 4x² + ? + 9.

Hướng dẫn giải

a) (2x – y )( 2x + y) = (2x)² – y² = 4x² – y²;

b) (x + 5y)(x – 5y) = x² – (5y)² = x² – 25y²;

c) x² + 4xy + 4y² = x² + 2 . x . 2y + (2y)² = (x + 2y)²;

d) (2x + 3)² = (2x)² + 2 . 2x . 3 + 3² = 4x² + 12x + 9.

Bài 3. Rút gọn biểu thức sau:

a) (2x – 1)² – (2x + 1)²;                              

b) (3x + 2y)² + (2x – 3y)².

Hướng dẫn giải

a) (2x – 1)² – (2x + 1)²

= [(2x – 1) – (2x + 1)][(2x – 1) + (2x + 1)]

= –2.4x

= –8x.

b) (3x + 2y)² + (2x – 3y)²

= (3x)² + 2.3x.2y + (2y)² + (2x)² – 2.2x.3y + (3y)²

= 9x² + 12xy + 4y² + 4x² –12xy + 9y²

= 13x² + 13y².

Bài 4. Chứng minh rằng với mọi số tự nhiên ta có:

(n + 2)² – n² chia hết cho 4.

Hướng dẫn giải

Ta có: (n + 2)² – n² = n² + 4n + 4 – n² = 4n + 4 = 4(n + 1)

Vì 4 ⁝ 4 suy ra 4(n + 1) ⁝ 4 với mọi số tự nhiên n.

Vậy (n + 2)² – n² chia hết cho 4 với mọi số tự nhiên n.

Học tốt Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Các bài học để học tốt Hiệu hai bình phương. Bình phương của một tổng hay một hiệu Toán lớp 8 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

---