Lý thuyết Số nguyên tố. Hợp số. Bảng số nguyên tố lớp 6 (hay, chi tiết)

Bài viết Lý thuyết Số nguyên tố. Hợp số. Bảng số nguyên tố lớp 6 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Số nguyên tố. Hợp số. Bảng số nguyên tố.

Lý thuyết Số nguyên tố. Hợp số. Bảng số nguyên tố lớp 6 (hay, chi tiết)

1. Số nguyên tố. Hợp số

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Ví dụ:

   + U(11) = {11; 1} nên 11 là số nguyên tố.

   + Số 15 có 4 ước là 1; 3; 5; 15 nên 15 là hợp số.

Chú ý:

• Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.

• Các số nguyên tố nhỏ hơn 10 là 2; 3; 5; 7.

2. Lập bảng các số nguyên tố nhỏ hơn 100

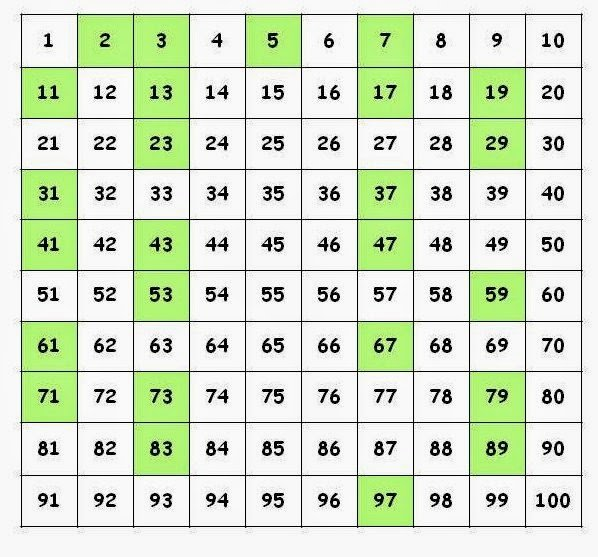
Số nguyên tố là các số trong khung màu xanh

Nhận xét: Số nguyên tố nhỏ nhất là số 2, đó là số nguyên tố chẵn duy nhất.

Câu 1: Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1

Lời giải:

Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số. Ta xét chỉ xét trường hợp số dư là 1 và 3.

     + Với mọi trường hợp số dư là 1 ta có a = 4n + 1

     + Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 – 1 = 4(n + 1) – 1 = 4m – 1

Câu 2: Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 thì (p – 1)(p + 1) chia hết cho 24.

Lời giải:

Ta có tích ba số tự nhiên liên tiếp chia hết cho 3:(p – 1)p(p + 1) ⋮ 3 mà p là số nguyên tố lớn hơn 3 nên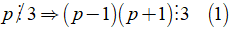

Mặt khác p là số nguyên tố lớn hơn 3 nên p là số lẻ, p – 1 và p + 1 là hai số chẵn liên tiếp có một số là bội của 4 nên tích của chúng chia hết cho 8     (2)

Từ (1), (2) suy ra (p – 1)(p + 1) chia hết cho hai số nguyên tố cùng nhau là 3 và 8

Vậy (p – 1)(p + 1) chia hết cho 24.

Bài 1. Trong các số sau, số nào là số nguyên tố: 2; 4; 5; 13; 15; 19; 25.

A. 2; 4; 19; 25.

B. 4; 13; 15; 25.

C. 2; 5; 13; 19.

D. 2; 4; 13; 19.

Hướng dẫn giải:

Đáp án đúng là: C

Các số 2; 5; 13; 19 chỉ chia hết cho 1 và chính nó nên chúng là các số nguyên tố.

Các số 4; 15; 25 là các hợp số:

+) 4 có các ước là {1; 2; 4};

+) 15 có các ước là {1; 3; 5, 15};

+) 25 có các ước là {1; 5; 25}.

Bài 2. Trong các khẳng định dưới đây, khẳng định nào là sai?

A. Số 2 là số nguyên tố bé nhất.

B. Mọi số tự nhiên lẻ đều là số nguyên tố.

C. Số tự nhiên lớn hơn 1 có nhiều hơn 2 ước dương được gọi là hợp số.

D. Tồn tại 2 số tự nhiên liên tiếp là số nguyên tố.

Hướng dẫn giải:

Đáp án đúng là: B

Khẳng định B là sai do số 2 vừa là số nguyên tố đồng thời cũng là một số chẵn.

Bài 3. Ba số tự nhiên lẻ liên tiếp đều là số nguyên tố là?

A. 3; 5; 7.

B. 5; 7; 9.

C. 1; 3; 5.

D. 7; 9; 11.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có các số nguyên tố nhỏ hơn 10 là: 2; 3; 5; 7.

Dễ dàng nhận thấy các số nguyên tố 3; 5; 7 là ba số tự nhiên lẻ liên tiếp.

Do đó, đáp án đúng là đáp án A.

Bài 4. Trong các khẳng định dưới đây, khẳng định nào là sai?

A. Số nguyên tố nhỏ hơn 10 là 2; 3; 5; 7.

B. 2 là số nguyên tố chẵn duy nhất.

C. Số 0 không là số nguyên tố cũng không là hợp số.

D. Số 1 là số nguyên tố bé nhất.

Hướng dẫn giải:

Đáp án đúng là: D

Số nguyên tố bé nhất là 2.

Bài 5. Trong các khẳng định dưới đây, khẳng định nào là sai?

A. 0 và 1 không phải là số nguyên tố cũng không phải là hợp số.

B. Cho số a > 1, a có 2 ước thì a là hợp số.

C. 2 là số nguyên tố chẵn duy nhất.

D. Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước là 1 và chính nó.

Hướng dẫn giải:

Đáp án đúng là: B

Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn 2 ước dương.

Bài 6. Trong các khẳng định dưới đây, khẳng định nào là đúng?

A. 0; 1 là các số nguyên tố.

B. 3; 5 là các số nguyên tố.

C. 1; 3; 5 là các các hợp số.

D. 7; 8 là các các hợp số.

Hướng dẫn giải:

Đáp án đúng là: B

Các số 3; 5; 7 là các số nguyên tố, 8 là hợp số.

0 và 1 không phải là số nguyên tố và cũng không phải là hợp số.

Bài 7. Kết quả của phép tính nào sau đây là số nguyên tố?

A. 15 – 5 + 3;

B. 7.2 + 1;

C. 14.6 : 4;

D. 6.4 – 12.2.

Hướng dẫn giải:

Đáp án đúng là: A

+ 15 – 5 + 3 = 13 là số nguyên tố.

+ 7.2 + 1 = 15 có các ước số là {1; 3; 5; 15} nên là hợp số.

+ 14.6 : 4 = 21 có các ước số là {1; 3; 7; 21} nên là hợp số.

+ 6.4 – 12.2 = 0 không phải là số nguyên tố hay hợp số.

Bài 8. Số nào sau đây là số nguyên tố?

A. 149;

B. 155;

C. 162;

D. 175.

Hướng dẫn giải:

Đáp án đúng là: A

Ta dễ dàng nhận thấy: 155; 175 đều chia hết cho 5, 162 chia hết cho 2 nên không phải là số nguyên tố.

149 có các ước số là {1; 149} nên là số nguyên tố.

Bài 9. Cho số tự nhiên hai chữ số có chữ số hàng chục là 6, chữ số hàng đơn vị là a. Với giá trị nào của a thì số đó là một số nguyên tố?

A. 1; 3.

B. 1; 5.

C. 3; 7.

D. 1; 7.

Hướng dẫn giải:

Đáp án đúng là: D

Để số đã cho là số nguyên tố thì a là chữ số lẻ, do đó a có thể nhận các giá trị {1; 3; 5; 7; 9}.

+ Nếu a ∈ {3; 9} thì số đã cho có tổng chia hết cho 3 nên không thỏa mãn.

+ Nếu a = 5 thì số đã cho chia hết cho 5 nên không thỏa mãn.

+ Nếu a = 1 thì số đã cho là 61 là số nguyên tố.

+ Nếu a = 7 thì số đã cho là 67 là số nguyên tố.

Bài 10. Cho số tự nhiên có hai chữ số, biết số đó là số nguyên tố và có chữ số hàng chục là 3. Số đã cho có thể là:

A. 37;

B. 34;

C. 35;

D. 39.

Hướng dẫn giải:

Đáp án đúng là: A

+ Tập hợp các ước số của 37 là {1; 37} nên là số nguyên tố.

+ Tập hợp các ước số của 34 là {1; 2; 17; 34} nên là hợp số.

+ Tập hợp các ước số của 36 là {1; 5; 7; 35} nên là hợp số.

+ Tập hợp các ước số của 39 là {1; 3; 13; 39} nên là hợp số.

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 6 có đáp án chi tiết hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 6 hay khác:

---