Tính khoảng cách từ một điểm đến một đường thẳng – Tổng hợp các dạng bài tập Toán 10 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 10.-Tính khoảng cách từ một điểm đến một đường thẳng
Tính khoảng cách từ một điểm đến một đường thẳng
Bài viết Tính khoảng cách từ một điểm đến một đường thẳng với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Tính khoảng cách từ một điểm đến một đường thẳng.
Tính khoảng cách từ một điểm đến một đường thẳng
1. Phương pháp giải
+ Cho đường thẳng d: ax + by + c = 0 và điểm M ( x0; y0). Khi đó khoảng cách từ điểm
M đến đường thẳng d là: d(M; d) = 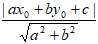
+ Cho điểm A( xA; yA) và điểm B( xB; yB) . Khoảng cách hai điểm này là :
AB = 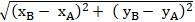
Chú ý: Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng d về dạng tổng quát.
2. Ví dụ minh họa
Ví dụ minh họa hoặc bài tập có giải
Ví dụ 1: Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:
A. 1
B. 2
C. 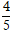
D. 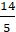
Hướng dẫn giải
Khoảng cách từ điểm M đến đường thẳng ( a) là:
d(M;a) = 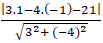
= 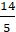
Chọn D.
Ví dụ 2: Khoảng cách từ điểm O đến đường thẳng d: 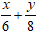
= 1 là:
A. 4,8
B. 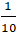
C. 1
D. 6
Hướng dẫn giải
Đường thẳng d: 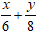
= 1 ⇔ 8x + 6y – 48 = 0
⇒ Khoảng cách từ điểm O đến đường thẳng d là :
d( O; d) = 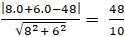
= 4,8
Chọn A.
Ví dụ 3: Khoảng cách từ điểm M(2; 0) đến đường thẳng
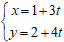
là:
A. 2
B. 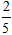
C. 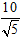
D. 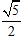
Hướng dẫn giải
+ Ta đưa đường thẳng d về dạng tổng quát:
(d) : 
⇒ Phương trình ( d) : 4( x – 1) – 3( y – 2) = 0 hay 4x – 3y + 2 = 0
+ Khoảng cách từ điểm M đến d là:
d( M; d) = 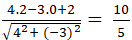
= 2
Chọn A.
Ví dụ 4. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng
(d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng:
A. R = 4
B. R = 6
C. R = 8
D. R = 10
Lời giải
Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng cách từ tâm đường tròn đến đường thẳng d chính là bán kính R của đường tròn
⇒ R= d(O; d) = 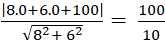
= 10
Chọn D.
Ví dụ 5 . Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:
A. 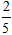
B. 1
C. 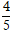
D. 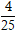
Lời giải
Khoảng cách từ điểm M đến đường thẳng d là:
d( M; d) = 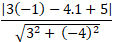
= 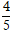
Chọn A.
Ví dụ 6. Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và
(b):
2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:
A. 2√10
B. 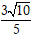
C. 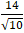
D. 2
Lời giải
Gọi A là giao điểm của hai đường thẳng ( a) và ( b) tọa độ điểm A là nghiệm hệ phương trình :
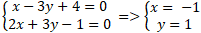
⇒ A( -1; 1)
Khoảng cách từ điểm A đến đường thẳng ∆ là :
d( A; ∆) = 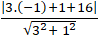
= 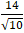
Chọn C
Ví dụ 7. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A( 1; 2) ; B(0; 3) và C(4; 0) . Chiều cao của tam giác kẻ từ đỉnh A bằng:
A. 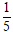
B. 3
C. 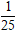
D. 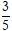
Lời giải
+ Phương trình đường thẳng BC:
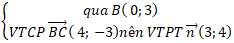
⇒ ( BC) : 3(x – 0) + 4( y – 3) = 0 hay 3x + 4y – 12 = 0
⇒ chiều cao của tam giác kẻ từ đỉnh A chính là khoảng cách từ điểm A đến đường thẳng BC.
d( A; BC) = 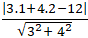
= 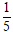
Chọn A.
Ví dụ 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; -4); B(1; 5) và C(3;1) . Tính diện tích tam giác ABC.
A. 10
B. 5
C. √26
D. 2√5
Lời giải
+ Phương trình BC:
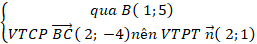
⇒Phương trình BC: 2( x – 1) + 1( y – 5) = 0 hay 2x + y – 7 = 0
⇒ d( A;BC) = 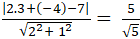
= √5
+ BC = 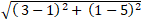
= 2√5
⇒ diện tích tam giác ABC là: S = 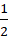
.d( A; BC).BC = 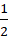
.√5.2√5 = 5
Chọn B.
Ví dụ 9: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng d1 : 4x – 3y + 5 = 0 và
d2: 3x + 4y – 5 = 0, đỉnh A( 2; 1). Diện tích của hình chữ nhật là:
A. 1.
B. 2
C. 3
D. 4
Lời giải
+ Nhận xét : điểm A không thuộc hai đường thẳng trên.
⇒ Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A(2; 1) đến hai đường thẳng trên, do đó diện tích hình chữ nhật bằng
S = 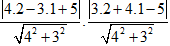
= 2 .
Chọn B.
Câu 1: Khoảng cách từ điểm M( 2;0) đến đường thẳng
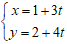
là:
A. 2
B. 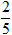
C. 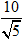
D. 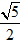
Lời giải:
Đáp án: A
+ Ta đưa đường thẳng d về dạng tổng quát:
(d) : 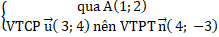
=> Phương trình (d) : 4( x – 1) – 3( y – 2) = 0 hay 4x – 3y + 2 = 0.
+ Khi đó khoảng cách từ M đến d là:
d(M, d)= 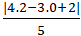
= 2
Câu 2: Đường tròn ( C) có tâm I ( -2; -2) và tiếp xúc với đường thẳng
d: 5x + 12y – 10 = 0. Bán kính R của đường tròn ( C) bằng:
A. R = 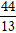
B. R = 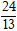
C. R = 44
D. R = 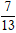
Lời giải:
Đáp án: A
Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng cách từ tâm đường tròn ( C) đến đường thẳng d chính là bán kính đường tròn.
=> R = d(I; d) = 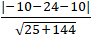
= 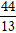
Câu 3: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a) : 4x – 3y + 5 = 0
và
(b) : 3x + 4y – 5 = 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
Đáp án: B
Ta thấy: điểm A không thuộc hai đường thẳng trên.
Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A đến hai đường thẳng trên.
Độ dài 2 cạnh là: d( A; a) = 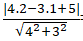
= 2; d(A; b) = 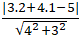
= 1
do đó diện tích hình chữ nhật bằng : S = 2.1 = 2
Câu 4: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích tam giác ABC ?
A. 3
B. 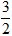
C. 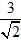
D. 147
Lời giải:
Đáp án: A
+ Phương trình đường thẳng AC: 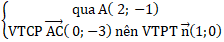
=> Phương trình AC: 1( x – 2) + 0.(y + 1) = 0 hay x – 2= 0..
+ Độ dài AC = 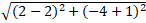
= 3 và khoảng cách từ B đến AC là:
d(B; AC) = 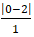
= 2
=> Diện tích tam giác ABC là : S = 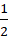
AC.d( B;AC) = 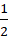
.3.2 = 3 .
Câu 5: Khoảng cách từ A(3; 1) đến đường thẳng
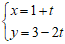
gần với số nào sau đây ?
A. 0, 85
B. 0,9
C. 0,95
D. 1
Lời giải:
Đáp án: B
Ta đưa đường thẳng d về dạng tổng quát:
(d): 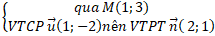
=> ( d): 2(x – 1) + 1( y – 3) = 0 hay 2x + y – 5 = 0
=> d(A, d) = 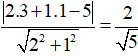
≈ 0,894
Câu 6: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng 4x – 3y + 5 = 0 và
3x + 4y + 5 = 0
đỉnh A(2; 1) . Diện tích của hình chữ nhật là
A. 6
B. 2
C. 3
D. 4
Lời giải:
Đáp án: A
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 4x – 3y + 5 = 0 là 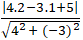
= 2
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 3x + 4y + 5 = 0 là 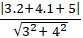
= 3
=> Diện tích hình chữ nhật bằng 2.3 = 6
Câu 7: Tính diện tích hình bình hành ABCD biết A( 1; -2) ; B( 2; 0) và D( -1; 3)
A. 6
B. 4,5
C. 3
D. 9
Lời giải:
Đáp án: D
+ Đường thẳng AB: 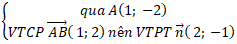
=> Phương trình AB: 2(x – 1) – 1(y + 2) = 0 hay 2x – y – 4 = 0
+ độ dài đoạn AB: AB = 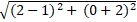
= √5
Khoảng cách từ D đến AB: d( D; AB)= 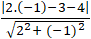
= 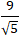
=> Diện tích hình chữ nhật ABCD là S = AB.d( D; AB) = √5.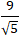
= 9
Câu 8: Tính khoảng cách từ giao điểm của hai đường thẳn (d) : x + y – 2 = 0 và
( ∆) : 2x + 3y – 5 = 0 đến đường thẳng (d’) : 3x – 4y + 11 = 0
A. 1
B. 2
C. 3
D. 4
Lời giải:
Đáp án: B
+ Giao điểm A của hai đường thẳng d và ∆ là nghiệm hệ phương trình
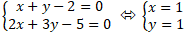
=> A( 1; 1)
+ Khoảng cách từ điểm A đến đường thẳng (d’) là :
d( A; d’) = 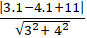
= 2
Bài 1. Tính khoảng cách từ điểm A(2; 3) đến đường thẳng d: 5x – 3y – 2 = 0.
Hướng dẫn giải:
Khoảng cách từ điểm A(2; 3) đến đường thẳng d: 5x – 3y – 2 = 0 là:
d(A; d) = 5.2−3.3−252+−32=3434.
Bài 2. Tính khoảng cách từ điểm O đến đường thẳng d: 3x + 2y – 1 = 0.
Hướng dẫn giải:
Khoảng cách từ điểm O đến đường thẳng d: 3x + 2y – 1 = 0 là:
d(O; d) = 5.0+2.0−152+22=2929.
Bài 3. Tính khoảng cách từ điểm A(–5; 2) đến đường thẳng d: 2x –y + 5 = 0.
Hướng dẫn giải:
Khoảng cách từ điểm A(–5; 2) đến đường thẳng d: 2x –y + 5 = 0 là:
d(A; d) = 2.−5−1.2+522+−12=755.
Bài 4. Tính khoảng cách từ điểm O đến đường thẳng d: x3+y2=5.
Hướng dẫn giải:
Đường thẳng d: x3+y2=5⇔x3+y2−5=0
Khoảng cách từ điểm O đến đường thẳng d: x3+y2=5 là:
d(O; d) = 03+02−5132+122=301313.
Bài 5. Tính khoảng cách từ điểm B(3; –5) đến đường thẳng {x = 2 + 3t; y = 5 – 2t}.
Hướng dẫn giải:
Xét đường thẳng d: {x = 2 + 3t; y = 5 – 2t}
2x + 3y = 2(2 + 3t) + 3(5 – 2t) = 4 + 6t + 15 – 6t = 19
Do đó 2x + 3y – 19 = 0
Khoảng cách từ điểm B(3; –5) đến đường thẳng d: 2x + 3y – 19 = 0 là:
d(B; d) = 2.3+3.−5−1922+32=281313.
Bài 6. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Tính Bán kính R của đường tròn (C).
Bài 7. Tính Khoảng cách từ giao điểm của hai đường thẳng a: x – 3y + 4 = 0 và b: 2x + 3y – 1 = 0 đến đường thẳng d: 3x + y + 16 = 0.
Bài 8. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (d1): 2x – 3y + 6 = 0 và (d2): 5x + 3y – 2 = 0, đỉnh A(3; 5). Tính diện tích của hình chữ nhật.
Bài 9. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a): 3x – 2y + 1 = 0 và (b): 4x + 3y – 3 = 0. Biết hình chữ nhật có đỉnh là giao điểm của hai đường thẳng a: 2x – 3y + 2 = 0 và b: 4x + 3y – 3 = 0. Tính diện tích của hình chữ nhật.
Bài 10. Đường tròn (C) có tâm I (–2; –2) và tiếp xúc với đường thẳng d: 5x + 12y – 10 = 0. Tính bán kính R của đường tròn (C).
Xem thêm các dạng bài tập Toán 10 có đáp án hay khác:
Lời giải bài tập lớp 10 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn