Biến cố xung khắc là gì? Bài tập biến cố xung khắc (cực hay, chi tiết)

Bài viết Biến cố xung khắc là gì? Bài tập biến cố xung khắc với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Biến cố xung khắc là gì? Bài tập biến cố xung khắc.

Biến cố xung khắc là gì? Bài tập biến cố xung khắc (cực hay, chi tiết)

1. Định nghĩa

– Định nghĩa: Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.

– Hai biến cố A và B là hai biến cố xung khắc nếu và chỉ nếu Ω_A ∩ Ω_B = ∅.

2. Quy tắc cộng xác suất

– Nếu hai biến cố A và B xung khắc thì xác suất để A hoặc B xảy ra là

    P(A ∪ B) = P(A) + P(B)

– Quy tắc cộng xác suất cho nhiều biến cố:

Cho k biến cố A₁, A₂, …, A_k đôi một xung khắc. Khi đó

    P(A₁ ∪ A₂ ∪ … ∪ A_k) = P(A₁) + P(A₂) + … + P(A_k)

3. Ví dụ

Ví dụ 1. Tung một con xúc xắc, gọi A là biến cố: “Xuất hiện mặt có chấm số chấm lớn hơn hoặc bằng 4”, B là biến cố: “Xuất hiện mặt có chấm số chấm nhỏ hơn hoặc bằng 2”.

Ta thấy hai biến cố và không cùng xảy ra, do đó A và B là hai biến cố xung khắc.

Ví dụ 2. Một hộp đựng 4 viên bi xanh,3 viên bi đỏ và 2 viên bi vàng.Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được hai viên bi cùng màu.

Hướng dẫn:

Có tất cả: 4 + 3 + 2 = 9 viên bi

X là biến cố “Chọn được 2 bi cùng màu”

Suy ra X = A ∪ B ∪ C và A, B, C là các biến cố đôi một xung khắc.

Theo quy tắc cộng xác suất

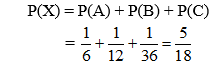
Ví dụ 3. Cho hai biến cố A và B. biết P(A) = 0,21; P(B) = 0,11 và P(A ∪ B) = 0,3. Hỏi A và B có phải là hai biến cố xung khắc không?

Hướng dẫn:

Ta có: P(A) + P(B) = 0,21 + 0,11 = 0,32 ≠ 0,3 = P(A ∪ B)

Suy ra P(A) + P(B) ≠ P(A ∪ B)

Theo quy tắc cộng xác suất của hai biến cố xung khắc, vậy hai biến cố A và B không xung khắc.

Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác: