Công thức logarit hay nhất | Toán lớp 12 – Tóm tắt công thức Toán lớp 12 quan trọng đầy đủ, chi tiết giúp học sinh dễ dàng nhớ được công thức Toán 12.-Công thức logarit hay nhất | Toán lớp 12
Công thức logarit hay nhất | Toán lớp 12
Công thức logarit hay nhất – Toán lớp 12
Công thức logarit hay nhất Toán lớp 12 sẽ giúp học sinh nắm vững công thức, biết cách làm bài tập
từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.

1. Lí thuyết
a. Định nghĩa: Cho 2 số dương a, b với a ≠ 1. Số x thỏa mãn đẳng thức ax = b được gọi là lôgarit cơ số a của b và kí hiệu là logab
ax = b ⇔ x = loga b
b. Các tính chất: Với a,b > 0; a ≠ 1 ta có

2. Các quy tắc tính
a. Lôgarit của một tích
– Định lí 1: Với các số dương a, x, y và a ≠ 1 ta có:
loga(x.y) = logax + logay
– Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:
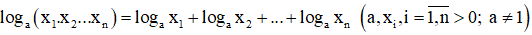
b. Lôgarit của một thương
– Định lí 2: Với các số dương a, x, y và a ≠ 1 ta có:
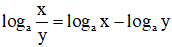
c. Lôgarit của một lũy thừa
– Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.
logabα = α.logab (a,b > 0; a ≠ 1; α ∈ R)
– Đặc biệt: 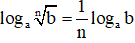
3. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên.
– Định lí 4: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1 ta có: 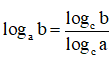
– Đặc biệt: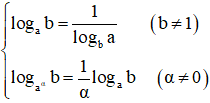
– Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: log10 x = log x
– Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: loge x = ln x
– Chú ý: Tìm số các chữ số của một lũy thừa:
Bài toán: Số aα có bao nhiêu chữ số?
Số các chữ số của aα chính là [log aα] + 1 (phần nguyên aα cộng 1)
– Ví dụ: Số 320 có [log 320] + 1 = 10 chữ số.
4. Các ví dụ
Ví dụ1. Tìm x biết
a. log2 x = 3
b. 3x = 4
c. log3 x = 4log3 a + 7log3 b (a,b > 0)
Lời giải:
a. log2 x = 3 ⇔ x = 23 ⇔ x = 8
b. 3x = 4 ⇔ x = log3 4 ⇔ x = 2
c. log3 x = 5log3 a + 7log3 b ⇔ log3 x = log3 a4 + log3 b7
⇔ log3 x = log3(a4.b7) ⇔ x = a4.b4
Ví dụ2. Cho log 2 5 = a. Tính log4 1250 theo a.
Lời giải:
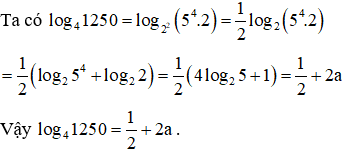
Ví dụ3. Cho log 3 15 = a và log 3 10 = b. Tính ANH theo a và b.
Lời giải:
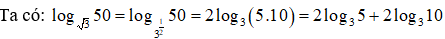
Ta thấy: log 3 15 = a ⇔ 1 + log3 5 = a ⇒ log3 5 = a – 1
Thay lại ta được: 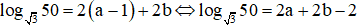
Ví dụ4. Cho a = log2 3, b = log3 5, c = log7 2. Tính log140 63 theo a, b, c
Lời giải:
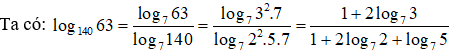
+) log7 3 = log2 3.log7 2 = a.c
+) log7 5 = log3 5.log7 3 = b.a.c
Thay vào ta được: 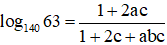
5. Luyện tập
Bài 1. Tính
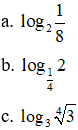
Bài 2. Tính
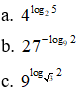
Bài 3. Tính
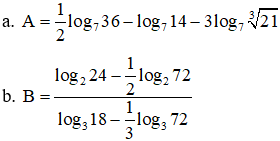
Bài 4. Tìm x biết
a. log5 x = 2log5 a – 3log5 b (a,b >0)
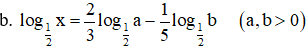
Bài 5. So sánh các cặp số sau
a. log3 5 và log7 4
b. log2 10 và log5 30
Bài 6.
a. log2 5 = a và log3 5 = bb Tính log5 5 theo a và b
b. Cho log2 3 = a; log5 3 = b. Hãy biểu diễn log6 45 theo a và b.
Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:



Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn