Công thức tính diện tích hình chữ nhật hay, chi tiết – Toán lớp 8

Công thức tính diện tích hình chữ nhật hay, chi tiết

Bài viết Công thức tính diện tích hình chữ nhật hay, chi tiết Toán lớp 8 hay nhất gồm 2 phần: Lý thuyết và Các ví dụ
áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Công thức tính diện tích hình chữ nhật hay, chi tiết.

I. Lí thuyết

Diện tích hình chữ nhật bằng tích hai kích thước của nó (tích của chiều dài và chiều rộng).

 S = a.b (đơn vị diện tích)

Với a là chiều dài, b là chiều rộng hình chữ nhật.

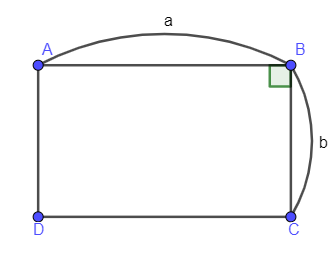
Hình chữ nhật ABCD có AB = a; BC = b

SA⁢B⁢C⁢D=A⁢B.B⁢C=a.b (đơn vị diện tích)

II. Các ví dụ:

Ví dụ 1: Tính diện tích hình chữ nhật có chiều dài là 5cm, chiều rộng là 3cm.

Lời giải:

Diện tích hình chữ nhật là:

S=5.3=15⁢c⁢m2

Vậy diện tích hình chữ nhật cần tính là 15cm².

Ví dụ 2: Một thửa đất hình chữ nhật có chu vi và 200m, chiều dài gấp ba lần chiều rộng. Tính diện tích thửa đất đó.

Lời giải:

Gọi chiều rộng của thửa đất hình chữ nhật là x (m) (x > 0).

Vì chiều dài gấp ba lần chiều rộng nên chiều dài thửa đất là 3x (m).

Chu vi thửa đất hình chữ nhật là: (x + 3x).2 (m)

Mà chu vi thửa đất là 200m nên ta có:

(x + 3x).2 = 200

⇔4⁢x⁢.2=200⇔8⁢x=200⇔x=200:8⇔x=25⁢m

Vì chiều dài bằng ba lần chiều rộng nên chiều dài thửa đất là: 3.25 = 75m

Diện tích thửa đất cần tính là:

S = 75.25 = 1875 (m²)

Ví dụ 3: Cho hình chữ nhật ABCD có AD = 7cm, BD = 25cm và O là giao điểm của hai đường chéo. Gọi M, N, P, Q theo thứ tự là trung điểm của OA, OB, OC, OD. Tính diện tích MNPQ.

Lời giải:

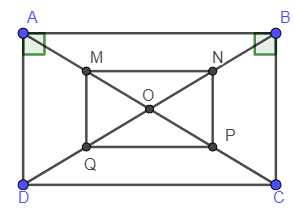
Vì ABCD là hình chữ nhật nên D⁢A⁢B^=90∘

Tam giác ABD vuông tại A ta có:

A⁢D2+A⁢B2=B⁢D2 (định lý Py – ta – go)

⇔72+A⁢B2=252⇔49+A⁢B2=625⇒A⁢B2=625-49⇒A⁢B=24⁢c⁢m

Ta có: M là trung điểm của OA; N là trung điểm của OB nên MN là đường trung bình của tam giác OAB

⇒MN//AB;MN=12AB (Tính chất)  (1)

Lại có: P là trung điểm của OC; Q là trung điểm của OD nên PQ là đường trung bình của tam giác OCD

⇒PQ//CD;PQ=12CD  (Tính chất)  (2)

Lại có ABCD là hình chữ nhật nên AB // CD; AB = CD (Tính chất)  (3)

Từ (1); (2); (3) ⇒MN//PQ;MN=PQ

Xét tứ giác MNPQ có:

MN // PQ

MN = PQ

Do đó tứ giác MNPQ là hình bình hành (dấu hiệu nhận biết).

Lại có M là trung điểm của OA; Q là trung điểm OD nên MQ là đường trung bình của tam giác OAD

 ⇒MQ//AD;MQ=12AD (Tính chất)

Mà A⁢B⊥A⁢D

Do đó M⁢Q⊥A⁢B. Mặt khác AB//MN(chứng minh trên) nên M⁢N⊥M⁢Q (quan hệ từ vuông góc đến song song).

⇒Q⁢M⁢N^=90∘

Xét hình bình hành MNPQ có:

Q⁢M⁢N^=90∘

Nên hình bình hành MNPQ là hình chữ nhật (dấu hiệu nhận biết).

Ta có: M⁢Q=12⁢A⁢D=12⁢.7=72⁢c⁢m

Diện tích hình chữ nhật MNPQ là:

S=M⁢Q.M⁢N=72⁢.12=42⁢c⁢m2.

Xem thêm các Công thức Toán lớp 8 quan trọng hay khác: