Cách chứng minh tứ giác nội tiếp lớp 9 (cực hay) – Chuyên đề Toán 9 tổng hợp phương pháp giải các dạng bài tập Toán 9 hay, chi tiết giúp bạn học tốt Toán 9.-Cách chứng minh tứ giác nội tiếp lớp 9 (cực hay)
Cách chứng minh tứ giác nội tiếp lớp 9 (cực hay)
Bài viết Cách chứng minh tứ giác nội tiếp lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách chứng minh tứ giác nội tiếp.
Cách chứng minh tứ giác nội tiếp lớp 9 (cực hay)
Đối với chứng minh tứ giác nội tiếp, ta sử dụng các dấu hiệu nhận biết sau:
+ Tứ giác có tổng hai góc đối bằng 180o.
+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.
Đối với bài toán tính góc, ta sử dụng các tính chất của tứ giác nội tiếp để tính toán.
Ví dụ 1 : Tính số đo các góc của tứ giác ABCD
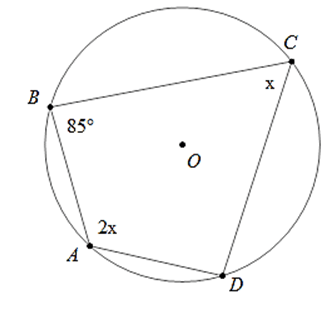
Hướng dẫn giải
Do ABCD là tứ giác nội tiếp nên 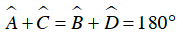
Vì 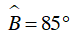 nên
nên 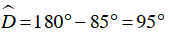
Ta có: 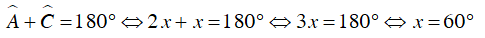
⇒ 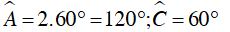
Vậy 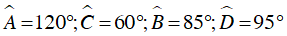 .
.
Ví dụ 2 : Cho đường tròn tâm O. Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC với đường tròn (B, C là hai tiếp điểm). Trên BC lấy điểm M, vẽ đường thẳng vuông góc với OM tại M, cắt AB và AC lần lượt tại E và D. Chứng minh các tứ giác EBOM và DCMO nội tiếp được trong đường tròn. Xác định tâm các đường tròn đó.
Hướng dẫn giải
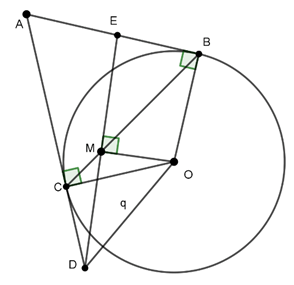
– Chứng minh tứ giác EBOM nội tiếp
Có OM ⊥ ME (gt) nên góc 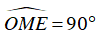
OB ⊥ BE (BE là tiếp tuyến của (O)) nên góc 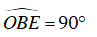
⇒ 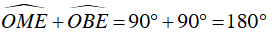
Tứ giác EBOM nội tiếp trong đường tròn đường kính OE.
– Chứng minh tứ giác DCMO nội tiếp
Có OM ⊥ DM (gt) nên góc 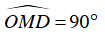
CD ⊥ OC (CĐ là tiếp tuyến của (O)) nên góc 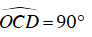
Nên M, C là hai đỉnh liên tiếp cùng nhìn OD dưới một góc 90o
⇒ Tứ giác DCMO nội tiếp trong đường tròn đường kính OD.
Ví dụ 3 : Qua điểm B nằm ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến BC và BD với đường tròn (O), (C, D là các tiếp điểm). Từ B vẽ cát tuyến BMN (M nằm giữa B và N, tia BN nằm giữa hai tia BC và BO), gọi H là giao điểm của BO và CD.
a. Chứng minh BM.BN = BH.BO.
b. Chứng minh tứ giác OHMN nội tiếp.
Hướng dẫn giải
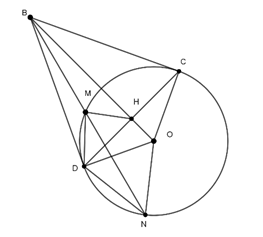
a. Ta có: BC = BD (tính chất hai tiếp tuyến cắt nhau)
OC = OD (bán kính đường tròn (O))
BO là đường trung trực của CD ⇒ BO ⊥ CD (1)
Xét ΔBMC và ΔBCN có:
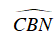 : chung
: chung
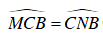 (cùng chắn cung
(cùng chắn cung 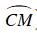 )
)
⇒ ΔBMC ∼ ΔBCN (g – g)
⇒ 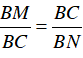 ⇒ BM.BN = BC2 (2)
⇒ BM.BN = BC2 (2)
Do (1) ta có △BCO vuông tại C, đường cao CH:
⇒ BC2 = BH.BO (hệ thức lượng trong tam giác vuông) (3)
Từ (2) và (3) ⇒ BM.BN = BH.BO.
b. Ta có: BM.BN = BH.BO (chứng minh trên)
⇒ 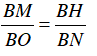
ΔBMO và ΔBHN có:
 : chung
: chung
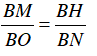
⇒ ΔBMO ∼ ΔBHN (c – g – c)
⇒ 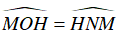 (hai góc tương ứng)
(hai góc tương ứng)
⇒ Tứ giác OHMN nội tiếp (hai góc bằng nhau cùng nhìn một cạnh).
Câu 1 : Cho hình vẽ sau, biết 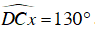 . Đáp án nào sau đây SAI
. Đáp án nào sau đây SAI
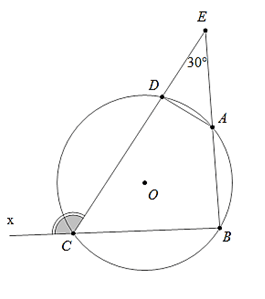
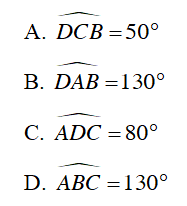
Hướng dẫn giải
Đáp án D
Ta có: 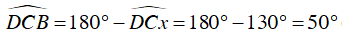 (hai góc kề bù)
(hai góc kề bù)
Ta lại có : 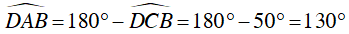 (ABCD là tứ giác nội tiếp đường tròn)
(ABCD là tứ giác nội tiếp đường tròn)
Lại có 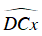 là góc ngoài của ΔECB
là góc ngoài của ΔECB
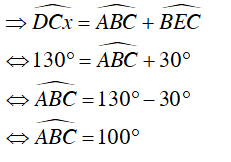
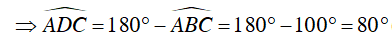 (ABCD là tứ giác nội tiếp đường tròn)
(ABCD là tứ giác nội tiếp đường tròn)
Vậy 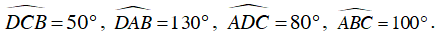
Câu 2 : Phát biểu nào sau đây sai ?
A. Tứ giác nội tiếp có 4 đỉnh cùng nằm trên cùng một đường tròn
B. Nếu một tứ giác có tổng hai góc đối bằng 180o thì tứ giác đó nội tiếp đường tròn.
C. Trong một tứ giác nội tiếp tổng hai góc bất kì bằng 180o
D. Hinh chữ nhật luôn nội tiếp đường tròn.
Hướng dẫn giải
Đáp án C
Trong tứ giác nội tiếp, tổng hai góc đối mới bằng 180o .
Câu 3 : Số đo góc A trong hình vẽ
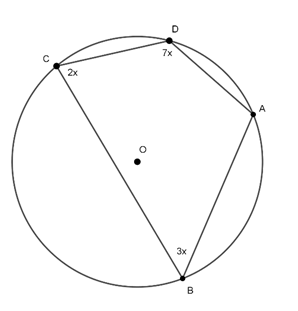
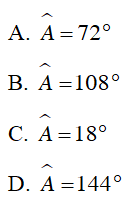
Hướng dẫn giải
Đáp án D
Ta có tứ giác ABCD nội tiếp đường tròn (O)
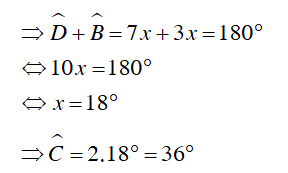
Mà 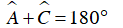
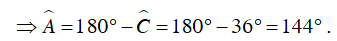
Câu 4 : Các hình nào sau đây nội tiếp đường tròn?
A. Hình thang, hình chữ nhật
B. Hình thang cân, hình bình hành
C. Hình thoi, hình vuông
D. Hình thang cân, hình chữ nhật, hình vuông
Hướng dẫn giải
Đáp án D
Hình thang cân, hình chữ nhật, hình vuông là các hình nội tiếp đường tròn.
Câu 5 : Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD. Tia AH cắt BC tại F. Số tứ giác nội tiếp có trong hình vẽ là:
A. 4
B. 6
C. 7
D. 8
Hướng dẫn giải
Đáp án B
Các tứ giác nội tiếp ADHE, BDHF, FHEC, BDEC, AEFB, ADFC.
Vậy có 6 tứ giác nội tiếp.
Câu 6 : Cho tam giác ABC vuông tại A, đường cao AH nội tiếp đường tròn (O;R) gọi I và K theo thứ tự là điểm đối xứng của H qua hai cạnh AB và AC. Khẳng định nào sau đây đúng?
A. Tứ giác AHBI nội tiếp đường tròn đường kính AB
B. Tứ giác AHCK nội tiếp đường tròn đường kính AC
C. Ba điểm I, A, K thẳng hàng
D. A, B, C đều đúng.
Hướng dẫn giải
Đáp án D
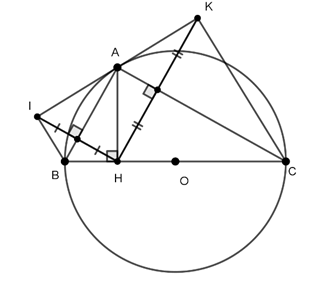
Ta có AH ⊥ BC 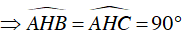
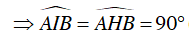 ( I đối xứng với H qua AB)
( I đối xứng với H qua AB)
Và 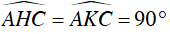 ( K đối xứng với H qua AC)
( K đối xứng với H qua AC)
Xét tứ giác AIBH, có: 
⇒ Tứ giác AIBH nội tiếp đường tròn đường kính AB
Xét tứ giác AKCH, có: 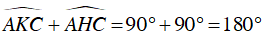
⇒ Tứ giác AKCH nội tiếp đường tròn đường kính AC
Ta lại có: 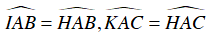 (do tính chất đối xứng)
(do tính chất đối xứng)
Mà 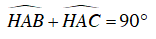
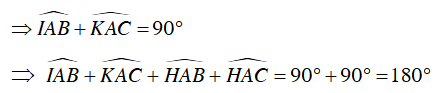
Suy ra ba điểm I, A, K thẳng hàng.
Do đó, cả A, B, C đều đúng.
Câu 7 : Cho hình vuông ABCD nội tiếp đường tròn (O;R). Độ dài cạnh hình vuông bằng:
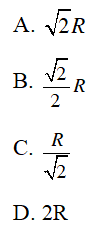
Hướng dẫn giải
Đáp án A
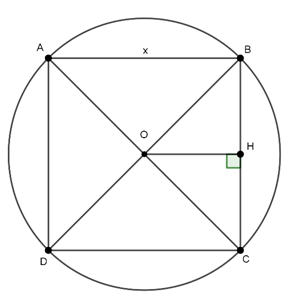
Đặt cạnh góc vuông là x
Ta có hình vuông ABCD nội tiếp (O; R)
Nên O là giao điểm của hai đường chéo, và OA = OB = OC = OD = R.
Kẻ OH vuông góc với BC.
Tam giác OBC vuông cân tại O, có OH ⊥ BC
⇒ H là trung điểm của BC
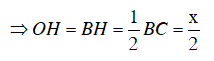
Xét tam giác OHB vuông tại H, có :
OB2 = OH2 + BH2
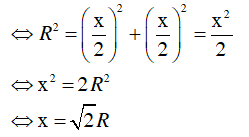
Vậy cạnh hình vuông có độ dài là 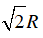 .
.
Câu 8 : Hình nào sau đây không nội tiếp đường tròn?
A. Hình vuông
B. Hình chữ nhật
C. Hình thoi
D. Hình thang cân
Hướng dẫn giải
Đáp án C
Hình vuông, hình chữ nhật và hình thang cân là các hình nội tiếp đường tròn.
Hình thoi là hình không nội tiếp đường tròn.
Câu 9 : Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính BD. Các đường chéo AC và BD cắt nhau tại E. Biết rằng AB = BC = 7,5cm và 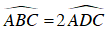 . Tính độ dài đường kính BD.
. Tính độ dài đường kính BD.
A. 11cm
B. 12cm
C. 14cm
D. 15cm
Hướng dẫn giải
Đáp án D
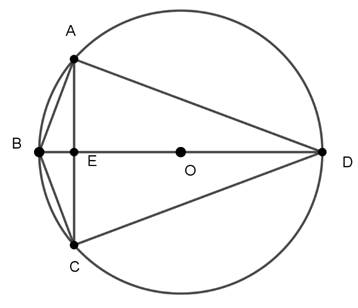
Do tứ giác ABCD nội tiếp (O) nên: 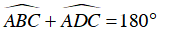
Mà 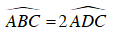
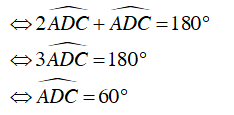
Ta có 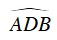 là góc nội tiếp chắn
là góc nội tiếp chắn 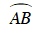
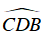 là góc nội tiếp chắn
là góc nội tiếp chắn 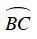
Mà 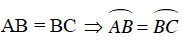
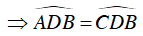 (hai góc nội tiếp chắn hai cung bằng nhau)
(hai góc nội tiếp chắn hai cung bằng nhau)
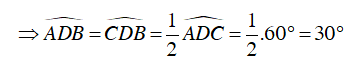
Ta có : 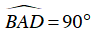 ( góc nội tiếp chắn nửa đường tròn)
( góc nội tiếp chắn nửa đường tròn)
⇒ tam giác ABD vuông tại A
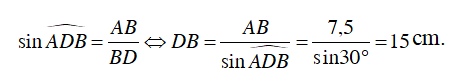
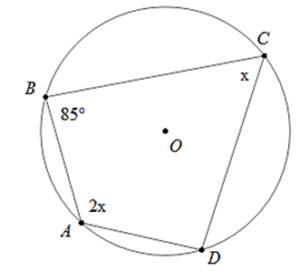
Câu 10 : Cho tứ giác ABCD nội tiếp trong đường tròn. Kéo dài AB về phía B một đoạn BE. Biết 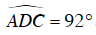 . Số đo góc EBC là:
. Số đo góc EBC là:
A.66
B.92
C.70
D.88
Hướng dẫn giải
Đáp án B
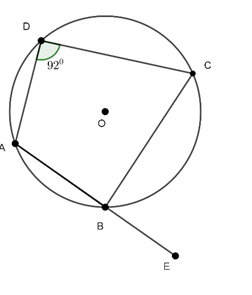
Vì tứ giác ABCD nội tiếp nên: 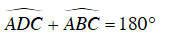
Mà: 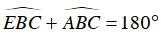 (hai góc kề bù)
(hai góc kề bù)
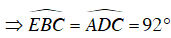 .
.
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có lời giải chi tiết hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn