Cách xác định vị trí tương đối của hai đường thẳng (cực hay) – Tổng hợp các dạng bài tập Toán 10 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 10.-Cách xác định vị trí tương đối của hai đường thẳng (cực hay)
Cách xác định vị trí tương đối của hai đường thẳng (cực hay)
Bài viết Cách xác định vị trí tương đối của hai đường thẳng với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách xác định vị trí tương đối của hai đường thẳng.
Cách xác định vị trí tương đối của hai đường thẳng (cực hay)
Cho hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0. Xét vị trí tương đối của hai đường thẳng d1 và d2:
+ Cách 1: Áp dụng trong trường hợp a1.b1.c1 ≠ 0:
Nếu 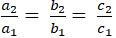
thì d1 ≡ d2.
Nếu 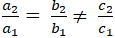
thì d1 // d2.
Nếu 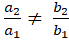
thì d1 cắt d2.
+ Cách 2: Dựa vào số điểm chung của hai đường thẳng trên ta suy ra vị trí tương đối của hai đường thẳng:
Giao điểm của hai đường thẳng d1 và d2( nếu có) là nghiệm hệ phương trình:
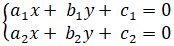
Nếu hệ phương trình trên có một nghiệm duy nhất thì 2 đường thẳng cắt nhau.
Nếu hệ phương trình trên có vô số nghiệm thì 2 đường thẳng trùng nhau.
Nếu hệ phương trình trên vô nghiệm thì 2 đường thẳng song song.
Ví dụ 1. Xét vị trí tương đối của hai đường thẳng d1: x- 2y+ 1= 0 và d2: -3x + 6y- 10= 0
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
Ta có: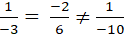
⇒ Hai đường thẳng đã cho song song với nhau.
Chọn B.
Ví dụ 2. Xét vị trí tương đối của hai đường thẳng d1: 3x – 2y – 6 = 0 và d2: 6x – 2y – 8 = 0.
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
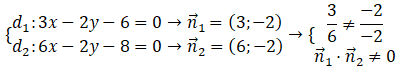
⇒ d1, d2 cắt nhau nhưng không vuông góc.
Chọn D.
Ví dụ 3. Xét vị trí tương đối của hai đường thẳng
d1: 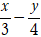
= 1 và d2: 3x + 4y – 10 = 0.
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
+ Đường thẳng d1 có VTPT n1→( 
; – 
) .
+ Đường thẳng d2 có VTPT n2→( 3; 4)
Suy ra: n1→.n2→ = 
.3 – 
.4 = 0
⇒ Hai đường thẳng đã cho vuông góc với nhau.
Chọn C.
Ví dụ 4. Đường thẳng nào sau đây song song với đường thẳng 2x + 3y – 1 = 0?
A. 4x + 6y + 10 = 0 .
B. 3x – 2y + 1 = 0
C. 2x – 3y + 1 = 0.
D. 4x + 6y – 2 = 0
Lời giải
Ta xét các phương án:
+ Phương án A:
Ta có: 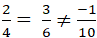
⇒ Hai đường thẳng này song song với nhau
+ Phương án B:
Ta có: 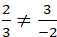
> Hai đường thẳng này cắt nhau.
+ Phương án C :
Ta có: 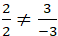
> Hai đường thẳng này cắt nhau.
+ Phương án D :
Ta có: 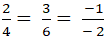
⇒ Hai đường thẳng này trùng với nhau
Chọn A.
Ví dụ 5. Với giá trị nào của m thì hai đường thẳng
a: 3x + 4y + 10 = 0 và b: (2m – 1)x + m2y + 10 = 0 trùng nhau?
A. m = ± 2
B. m = ± 1
C. m = 2
D. m = -2
Lời giải
Hai đường thẳng a và b trùng nhau khi và chỉ khi:
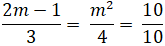
= 1
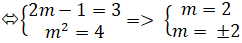
⇔ m = 2
Chọn C
Ví dụ 6. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng có phương trình
a: mx + (m-1)y + 2m = 0 và b: 2x + y – 1 = 0. Nếu a song song b thì:
A. m = 2
B. m = -1
C. m = – 2
D. m = 1 .
Lời giải
Ta có: hai đường thẳng a và b song song với nhau khi và chỉ khi :
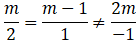
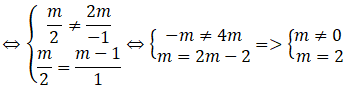
⇒ m = 2
Chọn A.
Ví dụ 7. Với giá trị nào của m thì hai đường thẳng (a) : 2x + y + 4 – m = 0
và ( b) : (m + 3)x + y + 2m – 1 = 0 song song?
A. m = 1
B. m = -1
C. m = 2
D. m = 3
Lời giải
+ Với m = 4 thì phương trình hai đường thẳng là:
( a) : 2x + y= 0 và ( b): 7x + y + 7 = 0
=> Với m = 4 hai đường thẳng a và b không song song với nhau.
+ Với m ≠ 4.
Để a // b khi và chỉ khi :
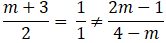
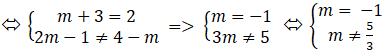
⇔ m = – 1
Vậy với m = -1 thì hai đường thẳng a và b song song với nhau.
Chọn B.
Ví dụ 8: Xét vị trí tương đối của hai đường thẳng (a): 2x – 3y + 2 = 0 và (b): y – 2 = 0.
A. Cắt nhau nhưng không vuông góc
B. Song song
C. Trùng nhau
D. Vuông góc
Lời giải
Giao điểm ( nếu có) của hai đường thẳng (a) và (b) là nghiệm hệ phương trình:
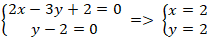
⇒ Hai đường thẳng đã cho cắt nhau tại A(2; 2). (1)
Lại có đường thẳng (a) có VTPT n→( 2; -3) và đường thẳng (b) có VTPT n’→( 0; 1)
⇒ n→.n’→ = 2.0 – 3.1 = -3 ≠ 0 (2)
Từ (1) và ( 2) suy ra hai đường thẳng đã cho cắt nhau nhưng không vuông góc.
Chọn A.
Ví dụ 9. Với giá trị nào của m thì hai đường thẳng ( a) : ( m- 3)x + 2y + m2 – 1 = 0
và (b): – x + my + m2 – 2m + 1 = 0 cắt nhau?
A. m ≠ 1.
B. m ≠ 1 và m ≠ 2
C. m ≠ 2
D. m ≠ 1 hoặc m ≠ 2
Lời giải
+ Nếu m = 0 thì hai đường thẳng đã cho trở thành:
(a) : – 3x + 2y – 1 = 0 và (b): – x + 1 = 0 .
Giao điểm của hai đường thẳng này là nghiệm hệ phương trình:
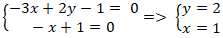
Vậy với m = 0 thì hai đường thẳng cắt nhau tại A( 1; 2) .
+ Nếu m ≠ 0. Để hai đường thẳng đã cho cắt nhau khi và chỉ khi:
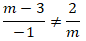
⇔ m(m – 3) ≠ – 2 ⇔ m2 – 3m + 2 ≠ 0
⇔ m ≠ 1 và m ≠ 2
Chọn B.
Ví dụ 10. Tìm tọa độ giao điểm của đường thẳng (a): 2x + 4y – 10 = 0 và trục hoành.
A.(0;2)
B. (0; 5)
C. (2;0)
D. (5;0)
Lời giải
Trục hoành có phương trình là: y = 0
Giao điểm của đường thẳng a và trục hoành nếu có nghiệm hệ phương trình :
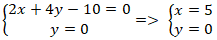
Vậy giao điểm của (a) và trục hoành là điểm A( 5; 0) .
Chọn D.
Ví dụ 11. Nếu ba đường thẳng (a): 2x + y- 4 = 0; (b) : 5x – 2y + 3 = 0 và
(c): mx + 3y – 2 = 0 đồng quy thì m nhận giá trị nào sau đây?
A. 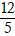
B. – 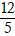
C. 12
D. – 12
Lời giải
Giao điểm của đường thẳng a và b là nghiệm hệ phương trình:
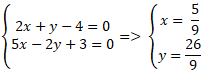
Vậy giao điểm của hai đường thẳng a và b là A( 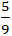
; 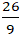
)
Để ba đường thẳng đã cho đồng quy khi và chỉ khi điểm A cũng thuộc đường thẳng c.
Thay tọa độ điểm A vào đường thẳng c ta được :
→ 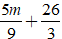
– 2 = 0 ⇔ m = -12
Chọn D.
Ví dụ 12. Với giá trị nào của m thì ba đường thẳng (a): 3x – 4y + 15 = 0;
(b): 5x + 2y – 1 = 0 và (c):mx – 4y + 15 = 0 đồng quy?
A. m = -5
B. m = 5
C. m = 3
D. m = -3
Lời giải
Giao điểm của đường thẳng a và b là nghiệm hệ phương trình:
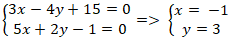
Vậy giao điểm của hai đường thẳng a và b là A( -1; 3)
Để ba đường thẳng đã cho đồng quy khi và chỉ khi điểm A cũng thuộc đường thẳng c.
Thay tọa độ điểm A vào đường thẳng c ta được :
– m – 4.3 + 15 = 0 ⇔ – m + 3 = 0 ⇔ m = 3
Chọn C.
Câu 1: Xác định vị trí tương đối của 2 đường thẳng sau đây: (a) : x – 2y + 1 = 0 và
(b): – 3x + 6y – 1 = 0
A. Song song.
B. Trùng nhau.
C. Vuông góc nhau.
D. Cắt nhau.
Lời giải:
Đáp án: A
Cách 1: Giải hệ phương trình thấy vô nghiệm nên hai đường thẳng song song
Cách 2: Đường thẳng a có vtpt n1→ = (1; -2) và (b) có vtpt n2→ = (-3; 6) .
Hai đường thẳng a và b có: 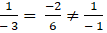
nên hai đường thẳng này song song.
Câu 2: Đường thẳng (a) :3x – 2y – 7 = 0 cắt đường thẳng nào sau đây?
A. ( d1) : 3x + 2y = 0
B. (d2) : 3x – 2y = 0
C. (d3): -3x + 2y – 7 = 0
D. (d4): 6x – 4y – 14 = 0
Lời giải:
Đáp án: A
+ Xét vị trí tương đối của đường thẳng a và d1 có:
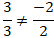
⇒ Hai đường thẳng này cắt nhau.
Câu 3: Hai đường thẳng (a): 4x + 3y – 18 = 0 và (b) : 3x + 5y – 19 = 0 cắt nhau tại điểm có toạ độ:
A. (3; 2)
B. ( -3; 2)
C. ( 3; -2)
D. (-3; -2)
Lời giải:
Đáp án: A
Gọi giao điểm của hai đường thẳng a và b là A.
Khi đó; tọa độ của điểm A là nghiệm hệ phương trình:
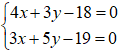
ta được 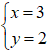
Vậy giao điểm của hai đường thẳng là A( 3; 2)
Câu 4: Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng d: y = 2x – 1
A. 2x – y + 5 = 0
B. 2x – y – 5 = 0
C. – 2x + y = 0
D. 2x + y – 5 = 0
Lời giải:
Đáp án: D
Ta đưa đường thẳng d về dạng tổng quát:
(d): y = 2x – 1 ⇔ (d): 2x – y – 1 = 0
Hai đường thẳng ( d): 2x – y – 1 = 0 và 2x + y – 5 = 0 không song song vì
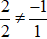
Câu 5: Hai đường thẳng (a) : mx + y = m + 1 và (b): x + my = 2 song song khi và chỉ khi:
A. m = 2
B. m = ± 1
C. m = -1
D. m = 1
Lời giải:
Đáp án: C
+ Nếu m= 0 hai đường thẳng trở thành : ( a) y = 1 và ( b) : x = 2.
Hai đường thẳng này cắt nhau nên với m= 0 thì không thỏa mãn .
+ Nếu m ≠ 0 .
Để hai đường thẳng a và b song song với nhau khi và chỉ khi :
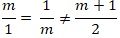
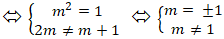
⇔ m = – 1
Vậy với m = -1 thì hai đường thẳng đã cho song song với nhau.
Câu 6: Tìm tất cả các giá trị của m để hai đường thẳng (a): 2x – 3my + 10 = 0 và
( b) : mx + 4y + 1 = 0 cắt nhau.
A. 1 < m < 10
B. m = 1
C. Không có m.
D. Với mọi m.
Lời giải:
Đáp án: D
+ Với m = 0 thì hai đường thẳng đã cho trở thành:
(a): x + 5 = 0 và (b) : 4y + 1 = 0
Giao điểm của hai đường thẳng a và b là nghiệm hệ phương trình :
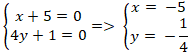
Vậy với m = 0 thì hai đường thẳng đã cho cắt nhau.
+ Với m ≠ 0.
Để hai đường thẳng đã cho cắt nhau khi và chỉ khi:
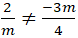
⇔ – 3m2 ≠ 8 hay m2 ≠ 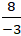
luôn đúng với m ≠ 0.
Vậy hai đường thẳng a và b luôn cắt nhau với mọi m.
Câu 7: Với giá trị nào của m thì hai đường thẳng (a): mx + y – 19 = 0 và
(b): ( m – 1).x + (m + 1).y – 20 = 0 vuông góc?
A. Với mọi m.
B. m = 2
C. Không có m.
D. m = 1
Lời giải:
Đáp án: C
Ta có đường thẳng ( a) nhận VTPT n→( m; 1)
Đường thẳng ( b) nhận VTPT n’→( m – 1; m + 1)
Để hai đường thẳng a và b vuông góc với nhau khi và chỉ khi hai VTPT của hai đường thẳng đó vuông góc với nhau.
⇔ n→.n’→ = 0 ⇔ m(m – 1) + 1(m + 1) = 0
⇔ m2 – m + m + 1 = 0 ⇔ m2 + 1 = 0 vô lí
vì m2 ≥ 0 với mọi m nên m2 + 1 > 0 với mọi m.
Vậy không có giá trị nào của m để hai đường thẳng đã cho vuông góc với nhau.
Câu 8: Với giá trị nào của m thì hai đường thẳng ( a): 3mx + 2y + 6 = 0 và
(b) : (m2 + 2)x + 2my + 6 = 0 cắt nhau?
A. m ≠ ±3
B. m ≠ ±2
C. mọi m
D. m ≠ ±1.
Lời giải:
Đáp án: D
+ Nếu m = 0 thì phương trình hai đường thẳng là :
(a) : 2y + 6 = 0 và (b):2x + 6 = 0.
Giao điểm của hai đường thẳng a và b là nghiệm hệ phương trình:
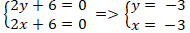
⇒ Với m = 0 thì hai đường thẳng đã cho cắt nhau.
+ Nếu m ≠ 0.
Để hai đường thẳng cắt nhau khi và chỉ khi:
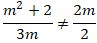
⇔ 2( m2 + 2) ≠ 6m2 ⇔ 4m2 ≠ 4
⇔ m2 ≠ 1 nên m ≠ ±1
Vậy để hai đường thẳng đã cho cắt nhau khi và chỉ khi m ≠ ±1
Câu 9: Tìm tọa độ giao điểm của hai đường thẳng (a) 7x – 3y – 1 = 0 và (b): x + 2 = 0.
A. (-2; 5)
B. (-2; -5)
C. (-2; -4)
D. (-4; 3)
Lời giải:
Đáp án: B
Giao điểm của hai đường thẳng a và b nếu có là nghiệm hệ phương trình:
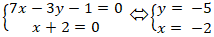
Vậy giao điểm của hai đường thẳng là M( -2; -5)
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình (a) : 3x – 4y + 15 = 0, ( b): 5x + 2y – 1 = 0 và (c) : mx – (2m – 1)y + 9m – 13 = 0. Tìm tất cả các giá trị của tham số m để ba đường thẳng đã cho cùng đi qua một điểm.
A. m = 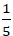
B. m= -5
C. m= – 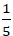
D. m= 5
Lời giải:
Đáp án: D
Giao điểm của đường thẳng a và b là nghiệm hệ phương trình:
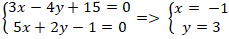
Vậy giao điểm của hai đường thẳng a và b là A( -1;3)
Để ba đường thẳng đã cho đồng quy khi và chỉ khi điểm A cũng thuộc đường thẳng c.
Thay tọa độ điểm A vào đường thẳng c ta được :
– m –(2m – 1).3 + 9m – 13 = 0 ⇔ – m – 6m + 3 + 9m – 13 = 0
⇔ 2m – 10 = 0 ⇔ m= 5.
Vậy ba đường thẳng đã cho đồng quy khi và chỉ khi m = 5.
Câu 11: Cho 3 đường thẳng d1 : 2x + y – 1 = 0 ; d2 : x + 2y + 1 = 0 và d3 : mx – y – 7 = 0. Để ba đường thẳng này đồng qui thì giá trị thích hợp của m là:
A. m= -6
B. m = 6
C. m = -5
D. m = 5
Lời giải:
Đáp án: B
+ Giao điểm của d1 và d2 là nghiệm của hệ 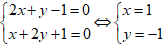
Vậy d1 cắt d2 tại A( 1 ; -1) .
+ Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên A thỏa phương trình của d3.
⇒ m.1 – (-1) – 7 = 0 ⇔ m = 6
Bài 1. Cho hai điểm A(3; 4) và B(4; 2). Viết phương trình đường trung trực của đoạn AB.
Bài 2. Cho điểm A(2; –3) và B(4; 7). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB.
Bài 3. Cho tam giác ABC cân tại A. Cho M(2; 3) là trung điểm của BC và B(–3 ; 4). Viết phương trình của đường thẳng AM.
Bài 4. Cho điểm A(1; 3) ; điểm B(m – 2; 2m + 3). Phương trình đường trung trực của AB là (d): 2x – 3y + 10 = 0. Tìm m.
Bài 5. Cho điểm A(m – 2; 3) và điểm B(–1; 2m). Phương trình đường trung trực của AB là ( d): 3x – 4y + 7 = 0. Tìm m.
Bài tập bổ sung
Bài 1. Xét vị trí tương đối của hai đường thẳng d1: 3x – y + 2= 0 và d2: –9x + 3y – 5= 0.
Bài 2. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng có phương trình a: mx + (2m – 3)y + 3m = 0 và b: x + 2y – 3 = 0. Tìm m để hai đường thẳng a và b song song với nhau.
Bài 3. Với giá trị nào của m thì hai đường thẳng (a) : 3x + 2y + 2 – 3m = 0 và (b) : 2mx + y + 2m – 3 = 0 song song với nhau?
Bài 4. Xét vị trí tương đối của hai đường thẳng (a): 3x – 5y + 2 = 0 và (b): 2y – 7 = 0.
Bài 5. Tìm tọa độ giao điểm của đường thẳng (d): 3x + 7y – 2 = 0 và trục hoành.
Xem thêm các dạng bài tập Toán 10 có đáp án hay khác:
Lời giải bài tập lớp 10 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn