Công thức lượng giác (Lý thuyết Toán lớp 11) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 11 Bài 2: Công thức lượng giác sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Công thức lượng giác (Lý thuyết Toán lớp 11) | Kết nối tri thức

Lý thuyết Công thức lượng giác

1. Công thức cộng

cos (a – b) = cosa cosb + sina sinb

cos (a + b) = cosa cosb – sina sinb

sin (a – b) = sina cosb – cosa sinb

sin (a + b) = sina cosb + cosa sinb

tan (a-b) = tana−tanb1+tanatanb

tan (a+b) = tana+tanb1-tanatanb

(giả thiết các biểu thức đều có nghĩa).

Ví dụ: Không dùng máy tính, hãy tính sin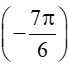 và tan 15°.

Hướng dẫn giải

Ta có

sin 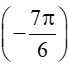= -sin7π6 = -sin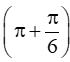

= -sinπcosπ6 – cosπsinπ6 = -0.32 – (-1).12 = 12.

Ta có

tan15^o = tan(60^o – 45^o) = tan60°−tan45°1+tan60°.tan45°

=3−11+3.1=3−13+1=2−3

2. Công thức nhân đôi

sin2a = 2sina cosa

cos2a = cos²a – sin²a = 2cos² – 1 = 1 – 2sin²a

tan2a = 2tana1−tan2a.

Chú ý: Từ công thức nhân đôi suy ra công thức hạ bậc:

cos2a=1+cos2a2

sin2a=1−cos2a2.

Ví dụ: Biết sinα = 25 và 0 < α < π2 . Tính sin2α ; cos2α và tan2α.

Hướng dẫn giải

Vì 0 < α < π2 nên cosα > 0.

Ta có:

sin²α + cos²α = 1 ⇒ cos²α = 1 – sin²α = 1-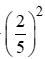= 2125

⇒ cosα = 215.

Ta có: sin2α = 2sinα cosα = 2.25.215=42125

cos2α = 1 – 2sin²α = 1 – 2.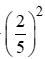= 1725

tanα=sinαcosα=22121

⇒ tan2α=2tanα1−tan2α=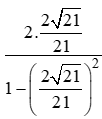=42117.

3. Công thức biến đổi tích thành tổng

cosacosb = 12[cos(a-b) + cos(a+b)]

sinasinb = 12[cos(a-b) – cos(a+b)]

sinacosb = 12[sin(a-b) + sin(a+b)].

Ví dụ: Tính giá trị của biểu thức

a) A = sin7π12cos5π12;

b) B = sinπ12sin7π12.

Hướng dẫn giải

a) Ta có:

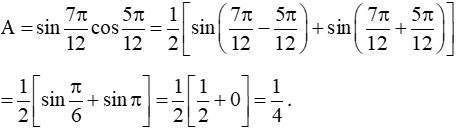
Vậy A = 14.

b) Ta có:

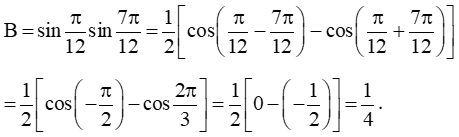
Vậy B = 14 .

4. Công thức biến đổi tổng thành tích

cosu + cosv = 2cosu+v2cosu-v2

cosu – cosv = -2sinu+v2sinu-v2

sinu + sinv = 2sinu+v2cosu-v2

sinu – sinv = 2cosu+v2sinu-v2.

Ví dụ: ChoA = cosπ17.cos4π17 và B = cos3π17 + cos5π17. Không dùng máy tính, tính giá trị của biểu thức AB.

Hướng dẫn giải

Ta có:

B = cos3π17 + cos5π17 = 2.cos3π17+5π172.cos3π17−5π172

= 2.cos4π17.cos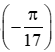 = 2cos4π17.cosπ17.

Suy ra AB=cosπ17.cos4π17cos3π17+cos5π17=cosπ17.cos4π172cos4π17.cosπ17=12 .

Bài tập Công thức lượng giác

Bài 1. Tính sin2a và tan2a biết cos a = 14 và 3π2<a<2π.

Hướng dẫn giải

Vì 3π2<a<2πnên sina < 0.

Ta có:

sin²a + cos²a = 1 ⇒ sin²a = 1 – cos²a = 1 – 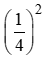= 1516

⇒ sina = −154.

Ta có: sin2a = 2sina cosa = 2.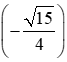.14 = -158

Ta có: tana = sinacosa=−15

⇒tan2a=2tana1−tan2a=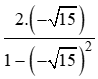==−215−14=157.

Bài 2. Tính

a) sin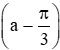 biết sin a = 34 và 0 < a < π2;

b) cos3π8.cosπ8 + sin3π8.sinπ8.

Hướng dẫn giải

a) Vì 0<a<π2 nên cosa > 0.

Ta có: sin²a + cos²a = 1 ⇒ cos²a = 1 – sin²a = 1-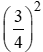=716

⇒ cosa = 74.

Vậy sin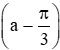=sinacosπ3−cosasinπ3=34.12−74.32=3−218 .

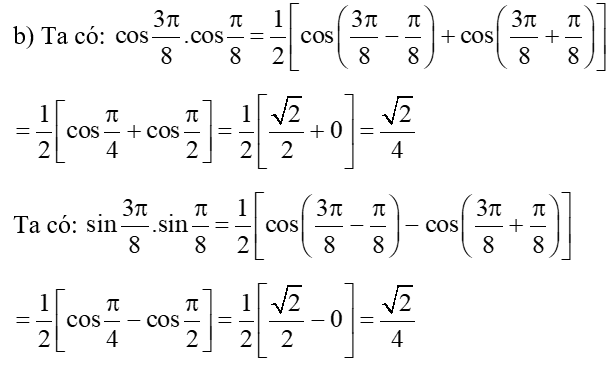
Suy ra: cos3π8.cosπ8+sin3π8.sinπ8=24+24=22.

Bài 3. Tính

a) cos(–15°) + cos255°;

b) sin13π24sin5π24.

Hướng dẫn giải

a) Ta có:

cos(-15^o) + cos255^o = 2.cos−15°+255°2.cos−15°−255°2

= 2.cos120^o.cos(135^o) = 2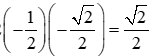

Vậy cos(–15°) + cos255° = 22.

b) Ta có:

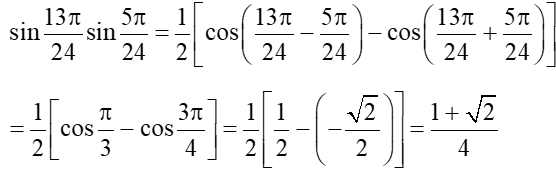
Vậy sin13π24sin5π24=1+24.

Học tốt Công thức lượng giác

Các bài học để học tốt Công thức lượng giác Toán lớp 11 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 11 hay khác:

Xem thêm các tài liệu học tốt lớp 11 hay khác:

---