Lý thuyết Đồ thị hàm số y = ax2 lớp 9 (hay, chi tiết) – Tổng hợp lý thuyết Toán 9 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm môn Toán 9.-Đồ thị hàm số y = ax2 (a ≠ 0): lý thuyết, các dạng bài tập có đáp án
Đồ thị hàm số y = ax2 (a ≠ 0): lý thuyết, các dạng bài tập có đáp án
Bài viết Lý thuyết Đồ thị hàm số y = ax2 lớp 9 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Đồ thị hàm số y = ax2.
Lý thuyết Đồ thị hàm số y = ax2 lớp 9 (hay, chi tiết)
1. Đồ thị hàm số y = ax2 (a ≠ 0)
Đồ thị của hàm số y = ax2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất cảu đồ thị.
2. Cách vẽ đồ thị hàm số y = ax2 (a ≠ 0)
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số y =ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
3. Ví dụ cụ thể
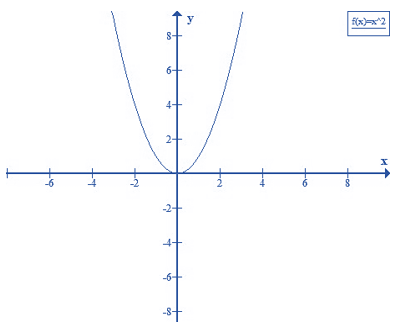
Câu 1: Vẽ đồ thị hàm số y = x2.
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = x2 | 0 | 1 | 1 | 4 | 4 |
Trên mặt phẳng tọa độ, lấy các điểm O(0;0): A(1; 1); B (-1; 1); C(2; 4) và D( -2;4) rồi lần lượt nối chúng để được đường cong như hình dưới đây.
Đồ thị của hàm số y = x2:
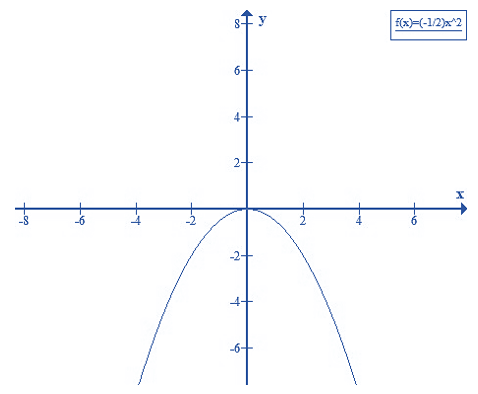
Câu 2: Vẽ đồ thị hàm số y = -(1/2)x2
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = -(1/2)x2 | 0 | -1/2 | -1/2 | -2 | -2 |
Đồ thị
Trên mặt phẳng tọa độ lấy các điểm
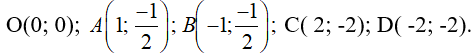
Nối các điểm đó ta được đường cong như hình vẽ dưới đây là đồ thị hàm số
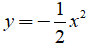
Câu 1: Cho hàm số y = ax2 . Tìm giá trị nhỏ nhất của y khi x đi từ -2017 đến 2018
Lời giải:
Ta thấy rằng hệ số a của đồ thị này dương, nên đồ thị có giá trị nhỏ nhất là y = 0 tại x = 0
Nhận thấy rằng trong khoảng -2017 đến 2018 đi qua hoành độ x = 0
Do đó giá trị nhỏ nhất của hàm số y = ax2 là y(0) = 0
Vậy giá trị nhỏ nhất của y bằng 0 tại x = 0
Câu 2: Cho hàm số 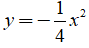 . Tìm giá trị nhỏ nhất của y khi đi từ đến 2.
. Tìm giá trị nhỏ nhất của y khi đi từ đến 2.
Lời giải:
Hệ số a của đồ thị này là số âm nên đồ thị này có giá trị lớn nhất là
* Khi x đi từ -1 đến 0 thì hàm số đồng biến nên trên đoạn [-1; 0] , hàm số đạt giá trị nhỏ nhất tại x = -1 và 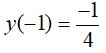
* Khi x đi từ 0 đến 2 thì hàm số nghịch biến nên hàm số đạt giá trị nhỏ nhất tại x = 2 trên đoạn
[ 0; 2] và y(2) = -1
* Suy ra, hàm số đạt giá trị nhỏ nhất tại x = 2 và 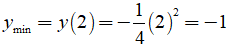
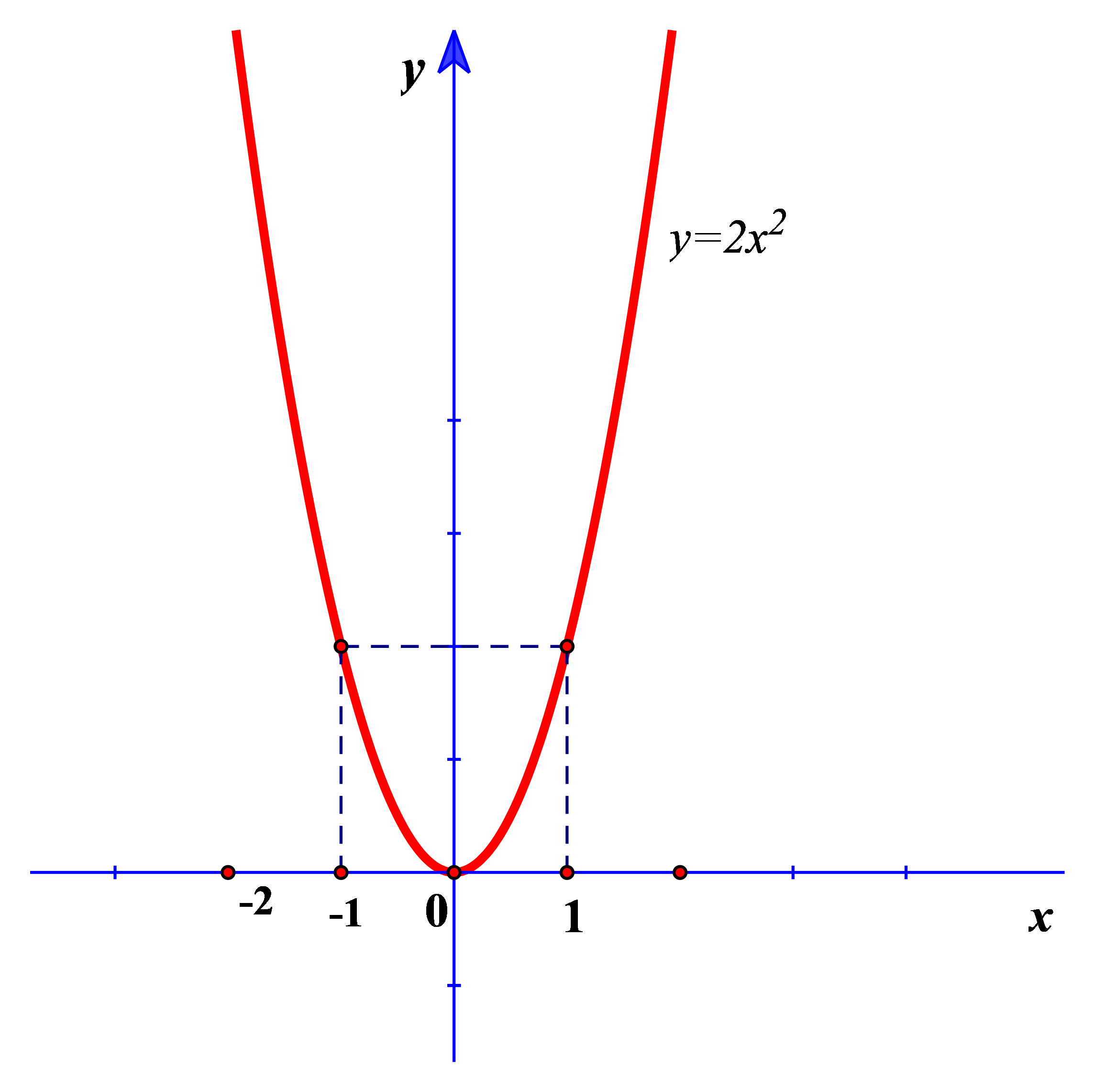
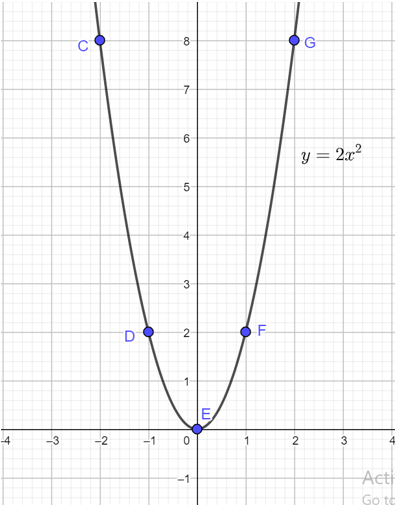
Câu 3: Trong mặt phẳng tọa độ Oxy , cho Parabol (P): y = 2x2 . Vẽ đồ thị parabol (P)
Lời giải:
Vẽ Parabol (P): y = 2x2
Bảng giá trị giữa x và y:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 8 | 2 | 0 | 2 | 8 |
Trên mặt phẳng tọa độ lấy các điểm A( – 2; 8); B(-1; 2) ; O(0; 0); C( 1;2) và D(2; 8).
Nối các điểm này ta được đường cong là đồ thị hàm số y = 2x2
Vẽ đúng đồ thị
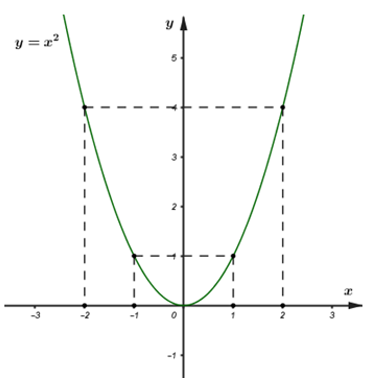
Bài 1. Cho hàm số y = x2 có đồ thị là (P). Hãy vẽ (P) trên hệ trục tọa độ.
Hướng dẫn giải:
Vẽ Parabol (P): y = x2
– Tập xác định: x ∈ R
– Bảng giá trị giữa x và y:
|
x |
– 2 |
– 1 |
0 |
1 |
2 |
|
y = 2x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm A(– 2; 4); B(– 1; 1); O(0; 0); C( 1; 1) và G(2; 4).
Nối các điểm này ta được đường cong là đồ thị hàm số y = x2.
– Vẽ đồ thị:
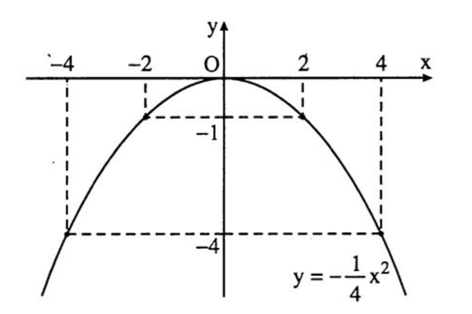
Bài 2. Cho hàm số có y=-14×2 đồ thị là (P). Hãy vẽ (P) trên hệ trục tọa độ.
Vẽ Parabol (P): y=-14×2
– Tập xác định: x ∈ R
– Bảng giá trị giữa x và y:
|
x |
– 4 |
– 1 |
0 |
2 |
4 |
| y=-14×2 |
– 4 |
– 1 |
0 |
– 1 |
– 4 |
Trên mặt phẳng tọa độ lấy các điểm A(– 4; – 4); B(– 2; – 1); O(0; 0); C(2; – 1) và G(4; – 4).
Nối các điểm này ta được đường cong là đồ thị hàm số y=-14×2.
– Vẽ đồ thị:
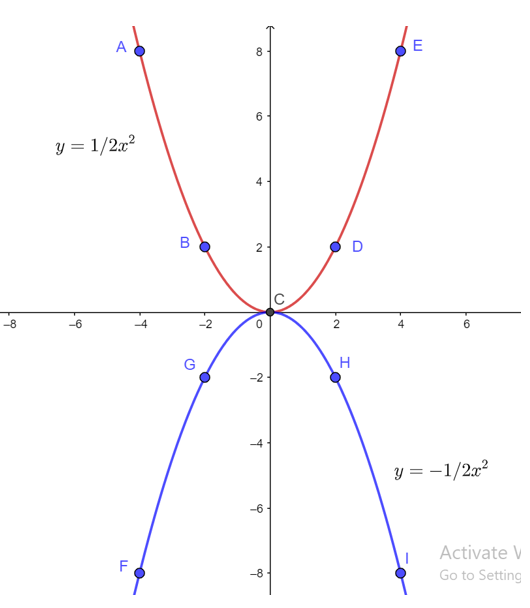
Bài 3. Cho hàm số y = ax2 (a ≠ 0) có đồ thị parabol (P). Xác định a để (P) đi qua điểm M(2;-1) và N(-2;1). Với giá trị a vừa tìm được hãy vẽ (P) trên mặt phẳng tọa độ.
Hướng dẫn giải:
– Thay x=2 và y = – 1 vào hàm số y = ax2.
Ta có: -1=a.(2)2 ⇔a=-12
Vậy đồ thị hàm số y=-12×2.
– Thay x = -2 và y = 1 vào hàm số y = ax2.
Ta có: 1 = a.(-2)2⇔a=12
Vậy đồ thị hàm số y=12×2.
– Vẽ đồ thị hàm số y=-12×2
Tập xác định: x ∈ R
Bảng giá trị giữa x và y:
|
x |
– 4 |
– 2 |
0 |
2 |
4 |
| y=-12×2 |
– 8 |
– 2 |
0 |
– 2 |
– 2 |
Trên mặt phẳng tọa độ lấy các điểm F(– 4; – 8); G(– 2; – 2); C(0; 0); H(2; – 2) và I(4; – 4).
Nối các điểm này ta được đường cong là đồ thị hàm số y=-12×2.
– Vẽ đồ thị hàm số y=12×2
Tập xác định: x ∈ R
Bảng giá trị giữa x và y:
|
x |
– 4 |
– 2 |
0 |
2 |
4 |
| y=12×2 |
8 |
2 |
0 |
2 |
8 |
Trên mặt phẳng tọa độ lấy các điểm A(– 4; 8); B(– 2; 2); C(0; 0); D(2; 2), E(4; – 8).
Nối các điểm này ta được đường cong là đồ thị hàm số y=-14×2.
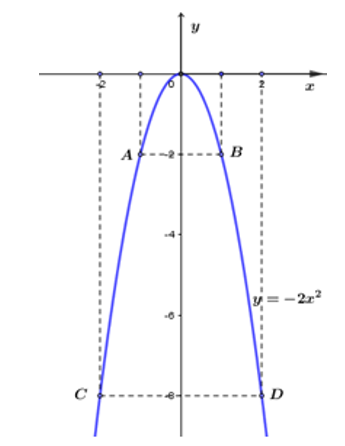
Bài 4. Cho hàm số y = ax2 (a ≠ 0) có đồ thị parabol (P)
a) Xác định a để (P) đi qua điểm A(-2;-4);
b) Với giá trị a vừa tìm được ở trên hãy vẽ (P) trên mặt phẳng tọa đô.
Hướng dẫn giải:
a) Thay x=-2 và y = – 4 vào hàm số y = ax2.
Ta có: -4 = a.(-2)2⇔a=-2
Vậy đồ thị hàm số y = – 2x2.
b) Với a = – 2 ta vẽ đồ thị hàm số
– Tập xác định: x ∈ R
– Bảng giá trị giữa x và y:
|
x |
– 2 |
– 1 |
0 |
1 |
2 |
|
y = –2x2 |
– 8 |
– 2 |
0 |
– 2 |
– 8 |
Trên mặt phẳng Oxy lấy các điểm C(– 2; – 8); A(– 1; – 2); O(0; 0); B( 1; – 2); G(2; – 8).
Nối các điểm này ta được đường cong là đồ thị hàm số y = –2x2.
– Vẽ đồ thị:
Bài 5. Cho hàm số y = 2x2 có đồ thị là (P).
a) Hãy vẽ (P) trên hệ trục tọa độ;
b) Tìm các điểm trên (P) có tung độ bằng 6.
Hướng dẫn giải:
a) Vẽ Parabol (P): y = 2x2
– Tập xác định: x ∈ R
– Bảng giá trị giữa x và y:
|
x |
– 2 |
– 2 |
0 |
1 |
2 |
|
y = 2x2 |
8 |
2 |
0 |
2 |
8 |
Trên mặt phẳng tọa độ lấy các điểm C(- 2; 8); D(-1; 2) ; E(0; 0); F(1;2) và G(2; 8).
Nối các điểm này ta được đường cong là đồ thị hàm số y = 2x2.
– Vẽ đồ thị:
b) Thay y = 6 vào y = 2x2 ta tìm được x=±3.
Vậy (P) có các điểm (3;6),(-3;6) khi tung độ bằng 6.
Bài 6. Trong mặt phẳng Oxy, hãy vẽ các đồ thị parabol (P).
a) y = x2;
b) y=-14×2;
c) y=12×2.
Bài 7. Cho hàm số y = – 2x2 là đồ thi parabol (P).
a) Vẽ (P) trên hệ trục tọa độ;
b) Trong các điểm A(1; 2), B(– 1; – 2), C(10; – 200) điểm nào thuộc (P), điểm nào không thuộc (P).
Bài 8. Đồ thị parabol (P): y = 2x2 hãy vẽ (P) trên mặt phẳng tọa độ và tìm các điểm thuộc (P) cách đều hai trục tọa độ.
Bài 9. Cho hàm số y = (m – 1)x2 (m ≠ 1) có đồ thị parabol (P).
a) Xác định m để (P) đi qua điểm A(-3;1);
b) Với giá trị m vừa tìm được hãy vẽ (P) trên mặt phẳng tọa độ.
Bài 10. Cho đồ thị parabol (P): y=13×2.
a) Vẽ (P) trên hệ trục tọa độ;
b) Tìm các điểm trên (P) có hoành độ bằng 1;
c) Tìm các điểm trên (P) có tung độ gấp đôi hoành độ.
Xem thêm lý thuyết và các dạng bài tập Toán lớp 9 có lời giải hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn