Nội dung bài viết
Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (10 đề) – Bộ 100 Đề thi Toán 9 năm học 2024 – 2025 học kì 1, học kì 2 chọn lọc, có đáp án giúp bạn ôn tập đạt điểm cao trong các bài thi Toán 9.-Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (10 đề)
Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (10 đề)
Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (10 đề)
Để học tốt Toán lớp 9, phần dưới đây liệt kê Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (10 đề), cực sát đề thi chính thức. Hi vọng bộ đề thi này sẽ giúp bạn ôn luyện & đạt điểm cao trong các bài thi, bài thi Toán lớp 9.
Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học
Phòng Giáo dục và Đào tạo …..
Đề kiểm tra 1 tiết chương 1 hình học Học kì 1
Môn: Toán lớp 9
Thời gian làm bài: 45 phút
(Đề 1)
Đề bài
Phần trắc nghiệm (3 điểm)
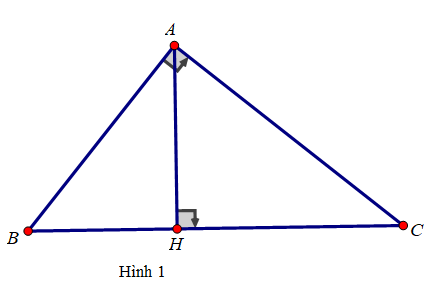
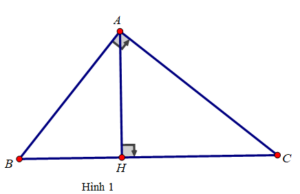
Câu 1: Dựa vào hình 1, hãy chọn câu đúng nhất:
A.BA2 = BC.CH B.BA2 = BC.BH
C.BA2 = BC2 + AC2 D.Cả 3 ý A,B,C đều sai
Câu 2: Dựa vào hình 1, độ dài của đoạn thẳng AH bằng
A.AB.AC B.BC.HB
C.√(HB.HC) D.BC.HC
Câu 3: Dựa vào hình 1, hệ thức nào sau đây là đúng:
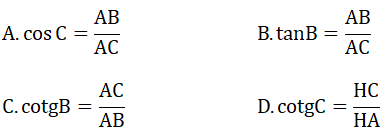
Câu 4: Cho tam giác ABC vuông tại A có ∠B =60o, AB = 6 cm. Kẻ đường cao AH. Độ dài đường cao AH là:
A.3 cm B.3√3 cm
C.6√3 cm D.Một kết quả khác
Câu 5: Đẳng thức nào sau đây không đúng
A.sin 37o = cos 53o
B.tan 30o.cotg 30o = 1
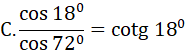
D.sinα + cosα=1
Câu 6: Giá trị của biểu thức: sin59o – cos31o bằng:
A.0 B.cos 28o C.sin 28o D.0,5
Phần tự luận (7 điểm)
Bài 1. (3 điểm) Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
a) Tính BC, ∠B, ∠C
b) Phân giác của góc A cắt BC tại D. Tính BD, CD
c) Từ D kẻ DE, DF vuông góc với AB, AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF
Bài 2. (3 điểm)
1) Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
2) Cho α là góc nhọn, chứng minh rằng:
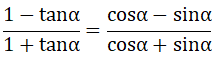
Bài 3. (1 điểm) Cho tam giác ABC có ∠A = 60o. Chứng minh rằng:
BC2 = AB2 + AC2 – AB.AC
Hướng dẫn giải
Phần trắc nghiệm (3 điểm)
| 1. B | 2.C | 3.D | 4.B | 5.D | 6.A |
Phần tự luận (7 điểm)
Bài 1.
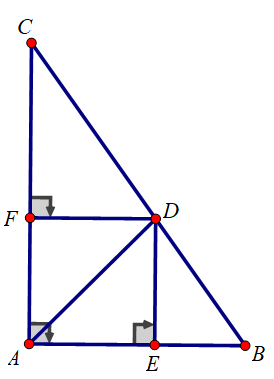
a) Xét tam giác ABC vuông tại A có:
BC2 = AB2 + AC2 = 62 + 82 = 100
⇒ BC = 10 (cm)
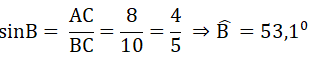
∠B + ∠C = 90o ⇒ ∠C = 90o – 53,1o = 36,9o
b) Do AD là tia phân giác của góc BAC, D ∈ BC nên ta có:
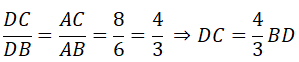
Mặt khác ta lại có:
DC + DB = BC ⇒ (4/3.BD) + BD = 10 ⇒ 7/3.BD = 10 ⇒ BD = 30/7 (cm)
Khi đó:
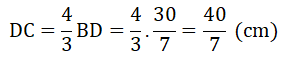
c) Xét tứ giác AEDF có:
∠(EAF) = ∠(AFD) = ∠(AED) = 90o
⇒ Tứ giác AEDF là hình chữ nhật
Lại có: ΔAFD vuông tại F, có ∠(FAD) = 45o
⇒ ΔAFD vuông cân tại F
⇒ AF = FD
⇒ tứ giác AEDF là hình vuông
Xét tam giác DEB vuông tại E có:
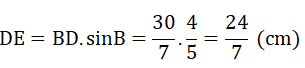
Chu vi hình vuông AEDF là:
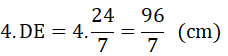
Diện tích hình vuông AEDF là:
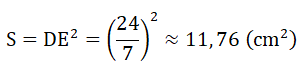
Bài 2.
1) Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin2α + cos2α = 1

Bài 3.
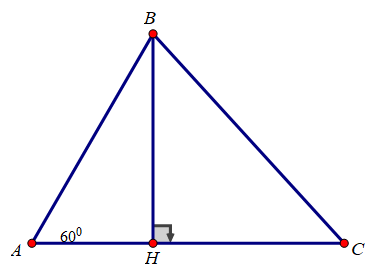
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60o
BH = AB.sin A = AB.sin 60o = (AB√3)/2
AH = AB.cos A = AB.cos 60o = AB/2
Xét tam giác BHC vuông tại H có:
BC2 = BH2 + HC2 = BH2 + (AC – AH)2
= BH2 + AC2 – 2.AC.AH + AH2
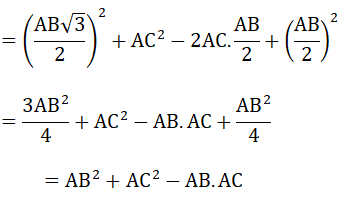
Vậy được điều phải chứng minh.
Phòng Giáo dục và Đào tạo …..
Đề kiểm tra 1 tiết chương 1 hình học Học kì 1
Môn: Toán lớp 9
Thời gian làm bài: 45 phút
(Đề 2)
Đề bài
Phần trắc nghiệm (3 điểm)
Câu 1: Tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, BC = 25cm, khi đó AB bằng:
A. 20cm B. 15cm C. 34cm D. 25/9
Câu 2: Giá trị của biểu thức sin 36o – cos54o bằng:
A. 0 B. 2 sin 36 C. 2 cos 54o D. 1
Câu 3: Tam giác DEF vuông tại D, biết DE = 25, góc E = 42o, thì độ dài của cạnh EF bằng bao nhiêu?
A. 18,58 B. 22,51
C. 16,72 D. Một kết quả khác.
Câu 4: Tam giác ABC vuông tại B, biết AB = 5, BC = 12 thì số đo của góc C bằng bao nhiêu?
A. 22o37′ B. 20o48′ C. 24o50′ D. 23o10′
Câu 5: Tam giác OPQ vuông tại P, đường cao PH Biết OP = 8, PQ = 15 thì PH bằng bao nhiêu?
A. 7,58 B. 5,78 C. 7,06 D. 6,07
Câu 6: Cho α + β = 90o, ta có:
A.sinα = sinβ
B.tanα.cotgα = √2/2
C.sin2α + cos2β = 1
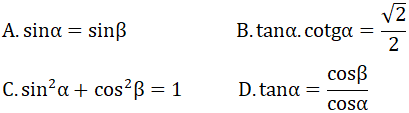
Phần tự luận (7 điểm)
Bài 1. (3 điểm) Đơn giản các biểu thức sau:
a) 1 – sin2α
b) sinα – sinα.cos2α
c)sin4α + cos4α + 2sin2αcos2α
d) sin220o + cos230o – sin240o – sin250o + cos260o + sin270o
Bài 2. (3 điểm ) Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Kẻ đường cao AH. Gọi P, Q lần lượt là hình chiếu của H trên AB và AC
a) Tính độ dài BH, CH, AH
b) Tính số đo góc B, góc C. Tính PQ
c) Tính AP.BP + AQ.AC
Bài 3. ( 1 điểm): Cho tam giác ABC nhọn, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Chứng minh rằng:
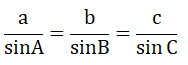
Hướng dẫn giải
Phần trắc nghiệm (3 điểm)
| 1.B | 2.A | 3.D | 4.A | 5.C | 6.D |
Phần tự luận (7 điểm)
Bài 1. Đơn giản các biểu thức sau:
a) 1 – sin2α = cos2α
b) sinα – sinα.cos2α
= sinα (1 – cos2α)
= sinα.sin2α
= sin3α
c) sin4α + cos4α + 2sin2αcos2α
= (sin2α + cos2α)2
= 1
d) sin220o + cos230o – sin240o – sin250o + cos260o + sin270o
= sin220o + cos230o – sin240o – cos240o + sin230o + cos220o
= (sin220o + cos220o) + (cos230o + sin230o ) – (sin240o + cos240o )
= 1 + 1 – 1
= 1
Bài 2.
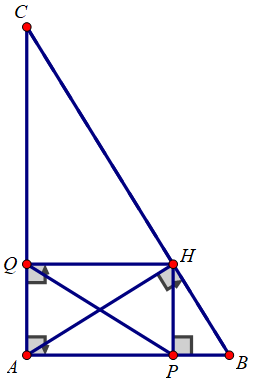
a) Xét tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
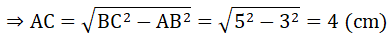
Tam giác ABC vuông tại A có AH là đường cao nên ta có:
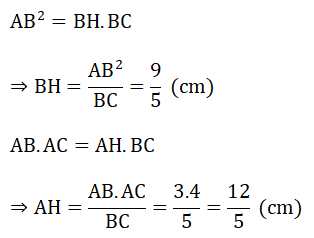
Ta có:
BH + CH = BC ⇒ CH = BC – BH = 5 – 9/5 = 16/5 (cm)
b)Xét tam giác ABC vuông tại A có:
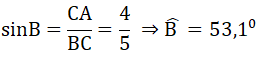
∠B + ∠C = 90o ⇒ ∠C = 90o – 53,1o = 36,9o
Xét tứ giác APHQ có:
∠(PAQ) = ∠(AQH) = ∠(APH) = 90o
⇒ Tứ giác APHQ là hình chữ nhật
⇒ PQ = AH = 12/5 (cm)
c) Xét tam giác AHB vuông tại H có HP là đường cao nên
AP.BP = HP2
Xét tam giác AHC có HQ là đường cao nên
AQ.AC = HQ2
Khi đó: AP.BP + AQ.AC = HP2 + HQ2 = PQ2 (ΔPHQ vuông tại H)
⇒ AP.BP + AQ.AC = (12/5)2 = 5,76 cm
Bài 3.
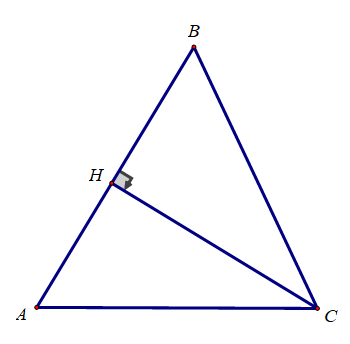
Kẻ đường cao CH của tam giác ABC. Ta có:
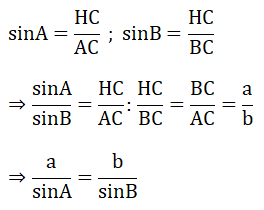
Chứng minh tương tự ta có:
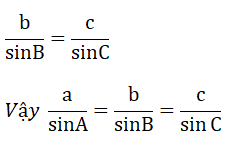
Phòng Giáo dục và Đào tạo …..
Đề kiểm tra 1 tiết chương 1 hình học Học kì 1
Môn: Toán lớp 9
Thời gian làm bài: 45 phút
(Đề 3)
Đề bài
Phần trắc nghiệm (3 điểm)
Câu 1: Cho tam giác ABC vuông tại A, hệ thức nào sau đây không đúng:
A.sinB = cos C B.sin2B + cos2B = 1
C.cosB = sin( 90o – B) D.sin C = cos (90o – B)
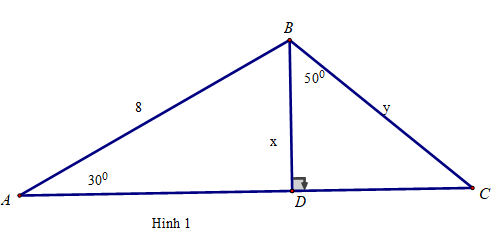
Câu 2: Dựa vào hình 1, tính x
A.x = 4 B.x = 4√3 C.x = (8√3)/3 D.x = 8
Câu 3: Dựa vào hình 1, tính y
A.y = 8,07 B.y = 7,98 C.y = 6,22 D.y = 5,81
Câu 4: Cho cosα = 0,8, khi đó:
A.tanα = 0,8 B.tanα – sinα = 0,15
C.cotgα = 0,75 D.sinα = 0,75
Câu 5: Tam giác ABC vuông tại A, AB = 20 cm, BC = 29 cm, ta có tanB=
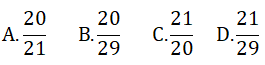
Câu 6:Cho tam giác ABC vuông tại A, đường cao AD. Biết DB = 4cm, CD = 9 cm. Độ dài của AD là:
A.6cm B.13 cm C.√6 cm D.2√13 cm
Phần tự luận (7 điểm)
Bài 1. (3 điểm) Đơn giản các biểu thức sau:
a) (1 – cosα)(1 + cosα)
b) tan2α – sin2α.tan2α
c) tan2α(2cos2α + sin2α – 1)
d) cos2 25o – cos2 35o + cos2 45o – cos2 55o + cos2 65o
Bài 2. : (3 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM ⊥ AB;HN ⊥ AC. Biết AB = 3cm; AC = 4 cm
a) Tính BC, BH, CH, MN
b) Tính số đo các góc của tam giác AMN
c) Tính diện tích tứ giác BMNC
Bài 3. (1 điểm) Cho tam giác ABC vuông tại A. Chứng minh rằng:
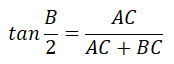
Hướng dẫn giải
Phần trắc nghiệm (3 điểm)
| 1.D | 2.A | 3.C | 4.B | 5.C | 6.A |
Phần tự luận (7 điểm)
Bài 1.
a) (1 – cosα)(1 + cosα)
= 1 – cos2α
= sin2α
b) tan2α – sin2α.tan2α
= tan2α(1 – sin2α)
= tan2α.cos2α
= sin2α
c) tan2α(2cos2α + sin2α – 1)
= tan2α(cos2α + cos2α + sin2α – 1)
= tan2α(cos2α + 1 – 1)
= tan2α.cos2α
= sin2α
d) cos225o – cos235o + cos245o-cos255o + cos265o
= cos225o – cos235o + cos245o-sin235o + sin225o
= (cos225o + sin225o ) – (cos235o + sin235o ) + cos245o
= 1 – 1 + 1/2
= 1/2
Bài 2.
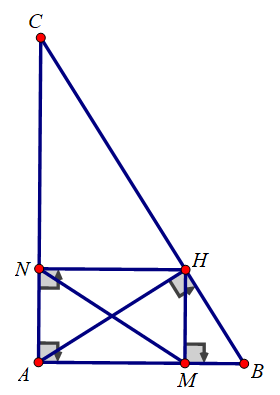
a) Xét tam giác ABC vuông tại A, đường cao AH có:
BC2 = AB2 + AC2 = 32 + 42 = 25 ⇒ BC = 5(cm)
AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)
BH + CH = BC⇒ CH = BC – BH = 5 – 1,8 = 3,2 (cm)
AH2= BH.CH ⇒ AH = √(BH.CH) = √(1,8.3,2) = 2,4 (cm)
Xét tứ giác AMHN có:
∠(MAN) = ∠(ANH) = ∠(AMH) = 90o
⇒ Tứ giác AMHN là hình chữ nhật
⇒ MN = AH = 2,4 (cm)
b) Xét tam giác AHB vuông tại H, HM là đường cao có:
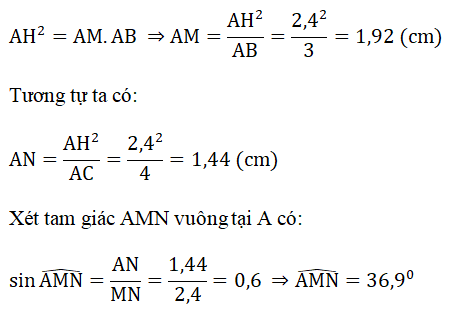
∠(AMN) + ∠(ANM ) = 90o ⇒ ∠(ANM ) = 90o– ∠(AMN) = 53,1o
c) Ta có:
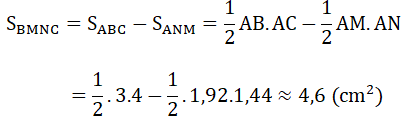
Bài 3.
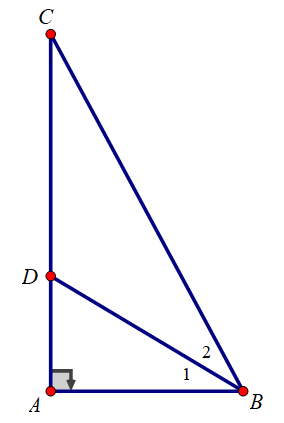
Vẽ đường phân giác BD của góc ABC
Xét tam giác ABD vuông tại A có:
tanB1 = DA/AB
Mặt khác ta có: BD là tia phân giác của góc ABC nên:
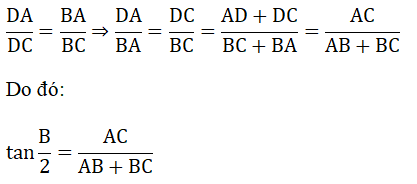
Xem thêm các đề kiểm tra, Đề thi Toán 9 chọn lọc, có đáp án hay khác:

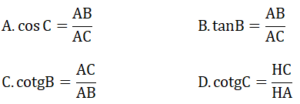
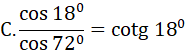

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn