Phương trình đường thẳng và cách giải bài tập (hay, chi tiết) – Tổng hợp phương pháp giải các dạng bài tập Toán lớp 10 giúp bạn biết cách làm bài tập Toán 10 dễ dàng hơn.-Phương trình đường thẳng và cách giải bài tập (hay, chi tiết)
Phương trình đường thẳng và cách giải bài tập (hay, chi tiết)
Với loạt Phương trình đường thẳng và cách giải bài tập sẽ giúp học sinh nắm vững lý thuyết, biết cách làm bài tập
từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 10.
Phương trình đường thẳng và cách giải bài tập
A. Lí thuyết tổng hợp
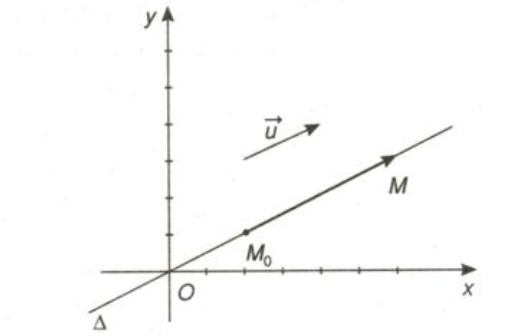
1. Các vectơ của đường thẳng:
+) Vectơ chỉ phương: Vectơ 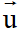 được gọi là vectơ chỉ phương của đường thẳng
được gọi là vectơ chỉ phương của đường thẳng 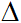 nếu
nếu 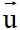 # 0 và giá của song song hoặc trùng với
# 0 và giá của song song hoặc trùng với  .
.
+) Vectơ pháp tuyến: Vectơ 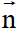 được gọi là vectơ pháp tuyến của đường thẳng
được gọi là vectơ pháp tuyến của đường thẳng  nếu
nếu 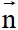 # 0 và vuông góc với vectơ chỉ phương của
# 0 và vuông góc với vectơ chỉ phương của  .
.
+) Nhận xét:
– Nếu 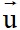 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng  thì k
thì k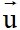 (k#0) cũng là một vectơ chỉ phương của
(k#0) cũng là một vectơ chỉ phương của  .
.
– Nếu 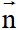 là một vectơ pháp tuyến của đường thẳng
là một vectơ pháp tuyến của đường thẳng  thì k
thì k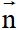 (k#0) cũng là một vectơ pháp tuyến của
(k#0) cũng là một vectơ pháp tuyến của  .
.
– Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương hoặc một vectơ pháp tuyến của đường thẳng đó.
– Một đường thẳng có vô số vectơ chỉ phương, vô số vectơ pháp tuyến.
2. Phương trình tổng quát của đường thẳng:
+) Định nghĩa: Phương trình  : ax + by + c = 0 (a2 + b2 # 0) là phương trình tổng quát của đường thẳng
: ax + by + c = 0 (a2 + b2 # 0) là phương trình tổng quát của đường thẳng  nhận
nhận 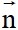 (a; b) làm vectơ pháp tuyến.
(a; b) làm vectơ pháp tuyến.
+) Các dạng đặc biệt:
 : ax + c = 0 , a#0
: ax + c = 0 , a#0 
 song song với Oy hoặc trùng với Oy khi a = 1 và c = 0.
song song với Oy hoặc trùng với Oy khi a = 1 và c = 0.
 : ay + c = 0 , a#0
: ay + c = 0 , a#0 
 song song với Ox hoặc trùng với Ox khi a = 1 và c = 0.
song song với Ox hoặc trùng với Ox khi a = 1 và c = 0.
 : ax + by = 0 , a2 + b2 # 0
: ax + by = 0 , a2 + b2 # 0 
 đi qua gốc tọa độ O(0; 0)
đi qua gốc tọa độ O(0; 0)
3. Phương trình tham số của đường thẳng:
+) Định nghĩa: Hệ 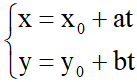 , a2 + b2 # 0 là phương trình tham số của đường thẳng
, a2 + b2 # 0 là phương trình tham số của đường thẳng  đi qua điểm A(x0;y0) và nhận vectơ
đi qua điểm A(x0;y0) và nhận vectơ 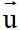 (a;b) làm vectơ chỉ phương, với t là tham số.
(a;b) làm vectơ chỉ phương, với t là tham số.
+) Chú ý:
Với mỗi t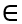 R thay vào phương trình tham số ta được một điểm M (x; y)
R thay vào phương trình tham số ta được một điểm M (x; y) 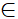

Một đường thẳng có vô số phương trình tham số.
– Phương trình chính tắc: 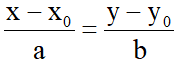 (a.b#0) là phương trình chính tắc của đường thẳng đi qua điểm M(x0;y0) và nhận
(a.b#0) là phương trình chính tắc của đường thẳng đi qua điểm M(x0;y0) và nhận 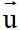 (a;b) làm vectơ chỉ phương.
(a;b) làm vectơ chỉ phương.
– Phương trình đoạn chắn: Đường thẳng cắt hai trục Ox và Oy lần lượt tại hai điểm A (a; 0), B (0; b) với a.b#0 có phương trình đoạn chắn là
cắt hai trục Ox và Oy lần lượt tại hai điểm A (a; 0), B (0; b) với a.b#0 có phương trình đoạn chắn là 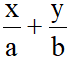 = 1.
= 1.
4. Hệ số góc:
Phương trình đường thẳng  đi qua điểm M(x0;y0) có hệ số góc k thỏa mãn: y – y0 = k(x-x0)
đi qua điểm M(x0;y0) có hệ số góc k thỏa mãn: y – y0 = k(x-x0)
+ Nếu  có vectơ chỉ phương
có vectơ chỉ phương 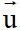 = (u1;u2) với u1#0 thì hệ số góc của
= (u1;u2) với u1#0 thì hệ số góc của là k =
là k = 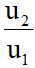
+ Nếu  có hệ số góc k thì
có hệ số góc k thì  có vectơ chỉ phương là
có vectơ chỉ phương là 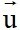 = (1;k)
= (1;k)
5. Vị trí tương đối của hai đường thẳng:
+) Xét hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0 với a12 + b12 # 0, a22 + b22 #0. Tọa độ giao điểm của hai đường thẳng đó là nghiệm của hệ phương trình:
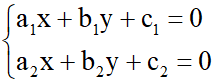 (1)
(1)
Ta có các trường hợp sau:
TH1: Hệ (1) có duy nhất một nghiệm (x0;y0) 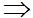 d1
d1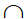 d2 tại M(x0;y0)
d2 tại M(x0;y0)
TH2: Hệ (1) có vô số nghiệm 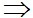 d1 trùng với d2
d1 trùng với d2
TH3: Hệ (1) vô nghiệm 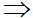 d1//d2
d1//d2
+) Chú ý: Với a2, b2, c2 #0 ta có:
d1 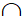 d2
d2 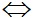
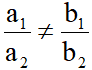
d1//d2 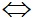
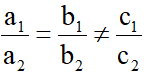
d1  d2
d2 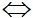
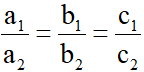
6. Góc giữa hai đường thẳng:
+ Cho hai đường thẳng d1: a1x + b1y + c1 = 0 có vectơ pháp tuyến 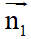 và d2: a2x + b2y + c2 = 0 có vectơ pháp tuyến
và d2: a2x + b2y + c2 = 0 có vectơ pháp tuyến 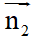 với a12 + b12 # 0, a22 + b22 #0, góc giữa hai đường thẳng đó được kí hiệu là (d1,d2), (d1,d2) luôn nhỏ hơn hoặc bằng
với a12 + b12 # 0, a22 + b22 #0, góc giữa hai đường thẳng đó được kí hiệu là (d1,d2), (d1,d2) luôn nhỏ hơn hoặc bằng 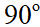 . Đặt
. Đặt 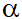 = (d1,d2) ta có:
= (d1,d2) ta có:
cos 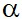 = |cos
= |cos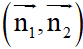 | =
| = 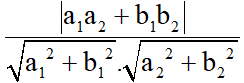
+ Chú ý:
d1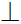 d2
d2 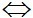
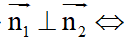 a1a2 + b1b2 = 0
a1a2 + b1b2 = 0
Nếu d1 và d2 có phương trình đường thẳng là y = k1x + m1 và y = k2x + m2 thì d1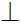 d2
d2 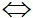 k1k2 = -1
k1k2 = -1
7. Khoảng cách từ một điểm đến một đường thẳng:
Trong mặt phẳng Oxy cho đường thẳng  có phương trình ax + by + c = 0 và điểm M(x0;y0). Khoảng cách từ điểm M đến đường thẳng
có phương trình ax + by + c = 0 và điểm M(x0;y0). Khoảng cách từ điểm M đến đường thẳng  được kí hiệu là d (M,
được kí hiệu là d (M, ) và tính bằng công thức:
) và tính bằng công thức:
d (M, ) =
) = 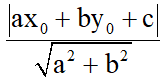
B. Các dạng bài.
Dạng 1: Cách viết các dạng phương trình đường thẳng.
Phương pháp giải:
a) Cách viết phương trình tổng quát của đường thẳng 
+ Tìm vectơ pháp tuyến 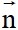 (a; b) của đường thẳng
(a; b) của đường thẳng 
+ Tìm một điểm M(x0;y0) thuộc 
+ Viết phương trình theo công thức: a(x-x0) + b(y-y0) = 0
+ Biến đổi thành dạng ax + by + c = 0
Nếu đường thẳng 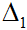 song song với đường thẳng
song song với đường thẳng 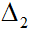 : ax + by + c = 0 thì
: ax + by + c = 0 thì 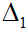 có phương trình tổng quát ax + by + c’ = 0, c ≠ c’.
có phương trình tổng quát ax + by + c’ = 0, c ≠ c’.
Nếu đường thẳng 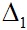 vuông góc với đường thẳng
vuông góc với đường thẳng 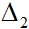 : ax + by + c = 0 thì có phương trình tổng quát -bx + ay + c’ = 0, c ≠ c’.
: ax + by + c = 0 thì có phương trình tổng quát -bx + ay + c’ = 0, c ≠ c’.
b) Cách viết phương trình tham số của đường thẳng
+ Tìm vectơ chỉ phương 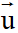 = (u1;u2) của đường thẳng
= (u1;u2) của đường thẳng 
+ Tìm một điểm M(x0;y0) thuộc 
+ Viết phương trình tham số: 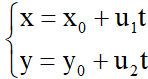
Nếu  có hệ số góc k thì
có hệ số góc k thì  có vectơ chỉ phương
có vectơ chỉ phương 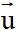 = (1;k)
= (1;k)
Nếu  có vectơ pháp tuyến
có vectơ pháp tuyến 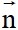 (a;b) thì
(a;b) thì  có vectơ chỉ phương
có vectơ chỉ phương 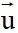 = (-b;a) hoặc
= (-b;a) hoặc 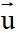 = (b;-a) và ngược lại.
= (b;-a) và ngược lại.
c) Cách viết phương trình chính tắc của đường thẳng  . (chỉ áp dụng khi có vectơ chỉ phương
. (chỉ áp dụng khi có vectơ chỉ phương 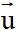 = (a;b) với a.b#0)
= (a;b) với a.b#0)
+ Tìm vectơ chỉ phương 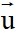 = (a;b) (a.b#0) của đường thẳng
= (a;b) (a.b#0) của đường thẳng 
+ Tìm một điểm M(x0;y0) thuộc 
+ Viết phương trình chính tắc: 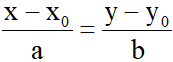
d) Cách viết phương trình đoạn chắn của đường thẳng  (chỉ áp dụng khi đường thẳng cắt hai trục Ox, Oy)
(chỉ áp dụng khi đường thẳng cắt hai trục Ox, Oy)
+ Tìm hai giao điểm của  với trục Ox, Oy lần lượt là A(a; 0), B(0; b)
với trục Ox, Oy lần lượt là A(a; 0), B(0; b)
+ Viết phương trình đoạn chắn 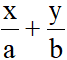 = 1 (a.b#0).
= 1 (a.b#0).
Ví dụ minh họa:
Bài 1: Cho đường thẳng d cắt trục Ox, Oy tại hai điểm A(0; 5) và B(6; 0). Viết phương trình tổng quát và phương trình đoạn chắn của đường thẳng d.
Lời giải:
Vì A(0; 5) và B(6; 0) thuộc đường thẳng d nên ta có 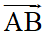 là vectơ chỉ phương của đường thẳng d.
là vectơ chỉ phương của đường thẳng d.
 = (6-0;0-5) = (6;-5)
= (6-0;0-5) = (6;-5)
 Vectơ pháp tuyến của d là
Vectơ pháp tuyến của d là 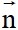 (5;6)
(5;6)
Chọn điểm A(0; 5) thuộc đường thẳng d, ta có phương trình tổng quát của đường thẳng d:
5.(x – 0) + 6.(y – 5) = 0
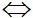 5x + 6y – 30 = 0
5x + 6y – 30 = 0
Vì đường thẳng d cắt trục Ox, Oy lần lượt tại hai điểm A(0; 5) và B(6; 0) nên ta có phương trình đoạn chắn: 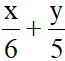 = 1.
= 1.
Bài 2: Cho đường thẳng d đi qua hai điểm M(5; 8) và N(3; 1). Viết phương trình tham số và phương trình chính tắc của đường thẳng d.
Lời giải:
Vì M(5; 8) và N(3; 1) thuộc đường thẳng d nên ta có 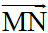 là vectơ chỉ phương của đường thẳng d, có
là vectơ chỉ phương của đường thẳng d, có 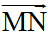 = (3 – 5; 1 – 8) = (-2; -7)
= (3 – 5; 1 – 8) = (-2; -7)
Chọn điểm N(3; 1) thuộc đường thẳng d ta có phương trình tham số của đường thẳng d: 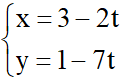
Chọn điểm M(5; 8) thuộc đường thẳng d ta có phương trình chính tắc của đường thẳng d: 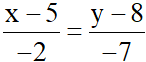
Dạng 2: Vị trí tương đối giữa hai đường thẳng.
Phương pháp giải:
Áp dụng lí thuyết về vị trí tương đối giữa hai đường thẳng: d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0 với a12 + b12 # 0, a22 + b22 #0.
Tọa độ giao điểm của hai đường thẳng đó là nghiệm của hệ phương trình:
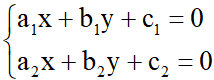 (1)
(1)
Với a2, b2, c2 #0 ta có:
d1 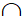 d2
d2 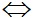
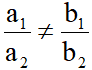
d1//d2 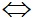
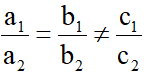
d1  d2
d2 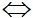
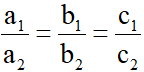
Ví dụ minh họa:
Bài 1: Xét vị trí tương đối của hai đường thẳng sau:
a) d1: 4x – 10y + 1 = 0 và d2 : x + y + 2 = 0.
b) d3: 12x – 6y + 10 = 0 và d4 : 2x – y + 5 = 0.
c) d5: 8x + 10y – 12 = 0 và d6 : 4x + 5y – 6 = 0.
Lời giải:
a) Xét hai đường thẳng d1: 4x – 10y + 1 = 0 và d2 : x + y + 2 = 0 có:
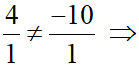 d1 và d2 cắt nhau.
d1 và d2 cắt nhau.
b) Xét hai đường thẳng d3: 12x – 6y + 10 = 0 và d4 : 2x – y + 5 = 0 có:
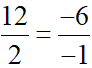 = 6 #
= 6 # 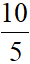 = 2
= 2  d3//d4
d3//d4
c) Xét hai đường thẳng d5: 8x + 10y – 12 = 0 và d6 : 4x + 5y – 6 = 0 có:
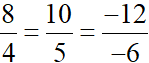 = 2
= 2 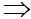 d5
d5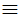 d6
d6
Bài 2: Cho hai đường thẳng: d1: x – 2y + 5 = 0 và d2 : 3x – y = 0. Tìm tọa độ giao điểm của d1 và d2.
Lời giải:
Xét tỉ số: 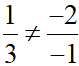
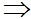 d1
d1  d2 . Gọi tọa độ giao điểm của d1 và d2 là M(x; y) với x và y là nghiệm của hệ phương trình:
d2 . Gọi tọa độ giao điểm của d1 và d2 là M(x; y) với x và y là nghiệm của hệ phương trình:
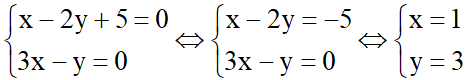
Vậy d1  d2 tại M (1; 3).
d2 tại M (1; 3).
Dạng 3: Tính góc giữa hai đường thẳng.
Phương pháp giải:
Áp dụng lí thuyết về góc giữa hai đường thẳng:
– Cho hai đường thẳng d1: a1x + b1y + c1 = 0 có vectơ pháp tuyến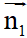 và d2: a2x + b2y + c2 = 0 có vectơ pháp tuyến
và d2: a2x + b2y + c2 = 0 có vectơ pháp tuyến 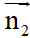 với a12 + b12 # 0, a22 + b22 #0, góc giữa hai đường thẳng được kí hiệu là (d1,d2), (d1,d2) luôn nhỏ hơn hoặc bằng
với a12 + b12 # 0, a22 + b22 #0, góc giữa hai đường thẳng được kí hiệu là (d1,d2), (d1,d2) luôn nhỏ hơn hoặc bằng 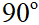 Đặt
Đặt 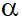 = (d1,d2) ta có:
= (d1,d2) ta có:
cos 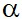 = |cos
= |cos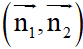 | =
| = 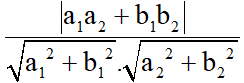
– Chú ý:
d1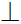 d2
d2 
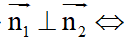 a1a2 + b1b2 = 0
a1a2 + b1b2 = 0
d1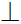 d2
d2 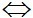
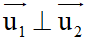
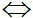 x1x2 + y1y2 = 0 với
x1x2 + y1y2 = 0 với 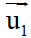 = (x1;y1) là vectơ chỉ phương của d1,
= (x1;y1) là vectơ chỉ phương của d1, 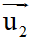 = (x2;y2)là vectơ chỉ phương của d2.
= (x2;y2)là vectơ chỉ phương của d2.
Nếu d1 và d2 có phương trình đường thẳng là y = k1x + m1 và y = k2x + m2 thì d1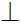 d2
d2 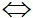 k1k2 = -1
k1k2 = -1
Ví dụ minh họa:
Bài 1: Cho hai đường thẳng d: 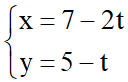 và d’:
và d’: 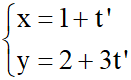 . Xác định số đo góc giữa d và d’.
. Xác định số đo góc giữa d và d’.
Lời giải:
Xét d: 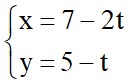 ta có vectơ chỉ phương của d là =
ta có vectơ chỉ phương của d là = 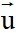 (-2; -1)
(-2; -1)
 Vectơ pháp tuyến của d là
Vectơ pháp tuyến của d là 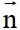 = (1; -2).
= (1; -2).
Xét d’: 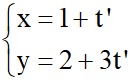 ta có vectơ chỉ phương của d’ là =
ta có vectơ chỉ phương của d’ là = 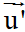 (1; 3)
(1; 3)
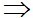 Vectơ pháp tuyến của d’ là =
Vectơ pháp tuyến của d’ là = 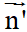 (-3; 1).
(-3; 1).
Ta có:
cos(d;d’) = |cos(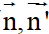 )| =
)| = 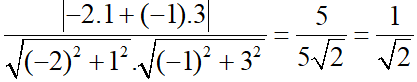
Góc giữa hai đường thẳng luôn nhỏ hơn hoặc bằng 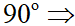 (d;d’) =
(d;d’) = 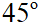 .
.
Bài 2: Cho hai đường thẳng d: 4x – 2y + 6 = 0 và d’: x + 2y + 1 = 0. Xác định số đo góc giữa d và d’.
Lời giải:
Xét d: 4x – 2y + 6 = 0 ta có vectơ pháp tuyến của d là 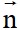 = (4; -2)
= (4; -2)
Xét d’: x + 2y + 1 = 0 ta có vectơ pháp tuyến của d’ là 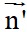 = (1; 2)
= (1; 2)
Ta có: 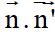 = 4.1 + (-2).2 = 0
= 4.1 + (-2).2 = 0
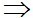 d
d  d’
d’
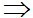 (d;d’) =
(d;d’) = 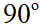
Dạng 4: Khoảng cách từ một điểm đến một đường thẳng.
Phương pháp giải:
Áp dụng lí thuyết về khoảng cách từ một điểm đến một đường thẳng: Trong mặt phẳng Oxy, đường thẳng  có phương trình ax + by + c = 0 và điểm M(x0;y0) . Khoảng cách từ điểm M đến đường thẳng
có phương trình ax + by + c = 0 và điểm M(x0;y0) . Khoảng cách từ điểm M đến đường thẳng  được kí hiệu là d (M,
được kí hiệu là d (M, ), tính bằng công thức:
), tính bằng công thức:
d (M, ) =
) = 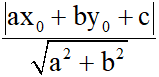
Ví dụ minh họa:
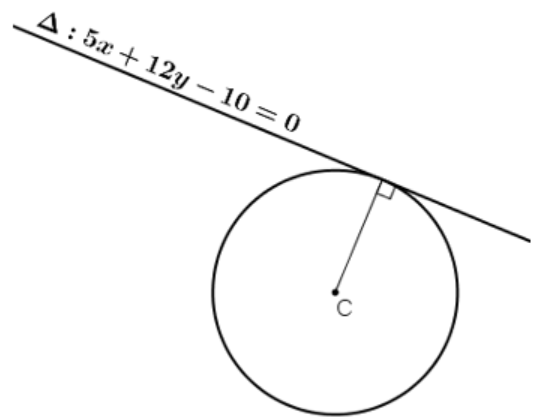
Bài 1: Tìm bán kính của đường tròn tâm C(-2; -2) . Biết đường tròn tiếp xúc với đường thẳng  : 5x + 12y -10 = 0.
: 5x + 12y -10 = 0.
Lời giải:
Vì đường tròn tiếp xúc với đường thẳng  : 5x + 12y – 10 = 0 nên ta có bán kính của đường tròn bằng khoảng từ tâm C đến đường thẳng
: 5x + 12y – 10 = 0 nên ta có bán kính của đường tròn bằng khoảng từ tâm C đến đường thẳng  . Ta có:
. Ta có:
R = d(C, ) =
) = 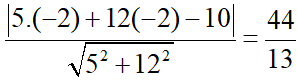
Bài 2: Cho điểm A (3; 6). Tìm khoảng cách từ A đến đường thẳng d: 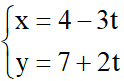
Lời giải:
Xét đường thẳng d: 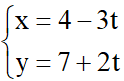 ta có vectơ chỉ phương của d là
ta có vectơ chỉ phương của d là 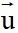 = (-3; 2)
= (-3; 2)
vectơ pháp tuyến của d là 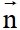 = (2; 3)
= (2; 3)
Chọn điểm M (4; 7) thuộc d ta có phương trình tổng quát của d là:
2.(x – 4) + 3.(y – 7) = 0
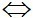 2x – 8 + 3y – 21 = 0
2x – 8 + 3y – 21 = 0
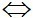 2x + 3y – 29 = 0
2x + 3y – 29 = 0
Khoảng cách từ A (3; 6) đến đường thẳng d là:
d(A;d) = 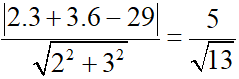
C. Bài tập tự luyện.
Bài 1: Viết phương trình tổng quát của đường thẳng d biết d đi qua 2 điểm A (3; 5) và B (4; 6).
Đáp án: d: – x + y = 2
Bài 2: Viết phương trình tham số của đường thẳng d’ biết d’ đi qua 2 điểm A (2; 7) và B (0; 5).
Đáp án: d’: 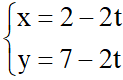
Bài 3: Viết phương trình chính tắc của đường thẳng d đi qua hai điểm M (1; 6) và N (2; 3)
Đáp án: d: 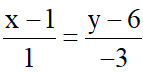
Bài 4: Viết phương trình đoạn chắn của đường thẳng d biết d song song với đường thẳng d’: 4x – 3y + 2 = 0 và d đi qua điểm (2; 3)
Đáp án: d: 4x – 3y + 1 = 0
Bài 5: Xét vị trí tương đối giữa đường thẳng d: 3x – 5y + 2 = 0 và đường thẳng d’: 3x – 5y = 0.
Đáp án: d // d’
Bài 6: Cho đường thẳng d: 2x – 6y + 3 = 0 và đường thẳng d’: x – m + 7 = 0. Tìm m để d // d’.
Đáp án: m = 3
Bài 7: Cho hai đường thẳng d: 6x – y = 0 và d’: 2x + 8y – 1 = 0. Tìm tọa độ giao điểm I của d và d’.
Đáp số: I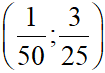
Bài 8: Cho hai đường thẳng d: 8x – 3y + 2 = 0 và d’: x = 4. Tìm số đo góc giữa d và d’.
Đáp án: (d;d’) = 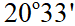
Bài 9: Cho điểm A (4; 7) và đường thẳng d’: x – 6 = 0. Tìm khoảng cách từ A đến đường thẳng d.
Đáp án: d (A, d’) = 2
Bài 10: Cho đường thẳng d: 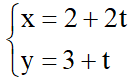 . Tìm m để khoảng cách giữa A (2; m) và đường thẳng d là 5.
. Tìm m để khoảng cách giữa A (2; m) và đường thẳng d là 5.
Đáp số: 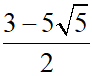
Bài tập bổ sung
Bài 1. Viết phương trình chính tắc của đường thẳng đi qua hai điểm A(1; 2) và B(2; 3).
Hướng dẫn giải
Ta có AB→=1; 1.
Phương trình chính tắc:
x−11=y−21 hay x – 1 = y – 2.
Bài 2. Viết phương trình tổng quát của đường thẳng đi qua hai điểm A(1; 2) và B(2; 3).
Hướng dẫn giải
Gọi phương trình tổng quát của đường thẳng là: y = ax + b.
Ta có 2=a+b3=2a+b hay a=1b=1.
Phương trình tổng quát của đường thẳng là y = x + 1.
Bài 3. Viết phương trình đường thẳng y = ax + b biết đường thẳng này đi qua 2 điểm A(–3, 2), B(5, –4).
Hướng dẫn giải
Ta có 2=−3a+b−4=5a+b hay a=−34b=−14.
Phương trình tổng quát của đường thẳng là y=−34x−14.
Bài 4. Viết phương trình đường thẳng y = ax + b biết đường thẳng này đi qua A (3; 1) và song song với đường thẳng y = –2x + m – 1.
Hướng dẫn giải
Do đường thẳng y = ax + b song song với đường thẳng y = –2x + m – 1 nên a = –2.
Phương trình đường thẳng trở thành y = –2x + b
đường thẳng này đi qua A (3; 1) nên 1 = (–2).3 + b hay b = 7.
x3 – x = 0 ⇔[x=0x=1
Phương trình tổng quát của đường thẳng là y = –2x + 7.
Bài 5. Cho đường thẳng AB với A(–2; 3) và B(4; –1). Hãy tìm phương trình chính tắc của đường thẳng AB.
Hướng dẫn giải
Ta có AB→=6;−4
Phương trình tham số:
x−−26=y−3−4 hay x+26=3−y4
Bài 6. Viết phương trình chính tắc của đường thẳng ∆ đi qua M(2; 3) và nhận vectơ u→=1;2 làm vectơ chỉ phương.
Bài 7. Cho đường thẳng d đi qua điểm M(3; 5) và N(2; 1). Viết phương trình tổng quát của đường thẳng d.
Bài 8. Cho đường thẳng d đi qua điểm M(3; 5) và N(2; 1). Viết phương trình tham số của đường thẳng d.
Bài 9. Cho đường thẳng d đi qua điểm M(3; 4) nhận vectơ u→1; 3 làm vectơ chỉ phương. Viết phương trình đường thẳng d dưới dạng chính tắc?
Bài 10. Cho parabol (P): y = –x2. Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc (P) và có hoành độ lần lượt là 1 và 2.
Xem thêm phương pháp giải các dạng bài tập Toán lớp 10 hay, chi tiết khác:
Lời giải bài tập lớp 10 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn