Phương sai, độ lệch chuẩn và cách giải (hay, chi tiết) – Tổng hợp phương pháp giải các dạng bài tập Toán lớp 10 giúp bạn biết cách làm bài tập Toán 10 dễ dàng hơn.-Phương sai, độ lệch chuẩn và cách giải (hay, chi tiết)
Phương sai, độ lệch chuẩn và cách giải (hay, chi tiết)
Với loạt Phương sai, độ lệch chuẩn và cách giải sẽ giúp học sinh nắm vững lý thuyết, biết cách làm bài tập
từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 10.
Phương sai, độ lệch chuẩn và cách giải
A. Lí thuyết.
1. Phương sai:
Phương sai của bảng thống kê số liệu x kí hiệu là sx2.
Công thức tính phương sai:
+ Trường hợp bảng phân bố tần số, tần suất: ni, fi, xi lần lượt là tần số, tần suất và giá trị của số liệu, n là số các số liệu thống kê, 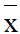 là số trung bình cộng của các số liệu thống kê đã cho.
là số trung bình cộng của các số liệu thống kê đã cho.
sx2 = 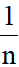 [n1(x1–
[n1(x1–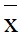 )2 + n2(x2–
)2 + n2(x2–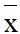 )2 + … + nk(xk–
)2 + … + nk(xk–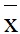 )2]
)2]
= f1(x1–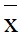 )2 + f2(x2–
)2 + f2(x2–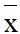 )2 + … + fk(xk–
)2 + … + fk(xk–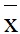 )2
)2
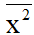 =
= 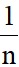 (n1x12 + n2x22 + … + nkxk2) = f1x12 + f2x22 + … + fkxk2
(n1x12 + n2x22 + … + nkxk2) = f1x12 + f2x22 + … + fkxk2
+ Trường hợp bảng phân bố tần số, tần suất ghép lớp: Trong đó ni, fi, ci lần lượt là tần số, tần suất, giá trị đại diện của lớp thứ i, n là số các số liệu thống kê, 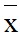 là số trung bình cộng của các số liệu thống kê đã cho.
là số trung bình cộng của các số liệu thống kê đã cho.
sx2 = 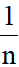 [n1(c1–
[n1(c1–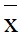 )2 + n2(c2–
)2 + n2(c2–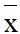 )2 + … + nk(ck–
)2 + … + nk(ck–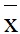 )2]
)2]
= f1(c1–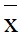 )2 + f2(c2–
)2 + f2(c2–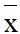 )2 + … + fk(ck–
)2 + … + fk(ck–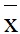 )2
)2
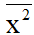 =
= 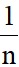 (n1c12 + n2c22 + … + nkck2) = f1c12 + f2c22 + … + fkck2
(n1c12 + n2c22 + … + nkck2) = f1c12 + f2c22 + … + fkck2
– Ý nghĩa của phương sai:
+ Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
+ Khi hai dãy số liệu có cùng đơn vị đo và có số trung bình bằng nhau hoặc xấp xỉ nhau, dãy có phương sai càng nhỏ thì mức độ phân tán (so với số trung bình) của các số liệu thống kê càng bé.
2. Độ lệch chuẩn:
Căn bậc hai của phương sai gọi là độ lệch chuẩn, kí hiệu sx. Ta có: sx = 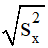
– Ý nghĩa độ lệch chuẩn: Độ lệch chuẩn cũng dùng đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình). Khi cần chú ý đến đơn vị đo ta dùng độ lệch chuẩn để đánh giá vì độ lệch chuẩn có cùng đơn vị đó với số liệu được nghiên cứu.
B. Phương pháp giải.
– Phương pháp tính phương sai, độ lệch chuẩn:
+ Tính trung bình cộng
+ Tính độ lệch của mỗi số liệu thống kê
+ Áp dụng các công thức:
sx = 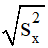
Đối với bảng phân bố tần số, tần suất:
sx2 = 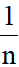 [n1(x1–
[n1(x1–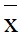 )2 + n2(x2–
)2 + n2(x2–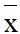 )2 + … + nk(xk–
)2 + … + nk(xk–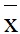 )2]
)2]
= f1(x1–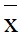 )2 + f2(x2–
)2 + f2(x2–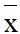 )2 + … + fk(xk–
)2 + … + fk(xk–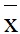 )2
)2
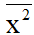 =
= 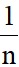 (n1x12 + n2x22 + … + nkxk2) = f1x12 + f2x22 + … + fkxk2
(n1x12 + n2x22 + … + nkxk2) = f1x12 + f2x22 + … + fkxk2
Đối với bảng phân bố tần số, tần suất ghép lớp:
sx2 = 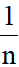 [n1(c1–
[n1(c1–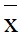 )2 + n2(c2–
)2 + n2(c2–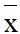 )2 + … + nk(ck–
)2 + … + nk(ck–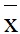 )2]
)2]
= f1(c1–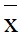 )2 + f2(c2–
)2 + f2(c2–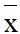 )2 + … + fk(ck–
)2 + … + fk(ck–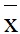 )2
)2
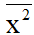 =
= 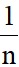 (n1c12 + n2c22 + … + nkck2) = f1c12 + f2c22 + … + fkck2
(n1c12 + n2c22 + … + nkck2) = f1c12 + f2c22 + … + fkck2
C. Ví dụ minh họa.
Bài 1: Điểm trung bình các môn học của học sinh được cho trong bảng sau:
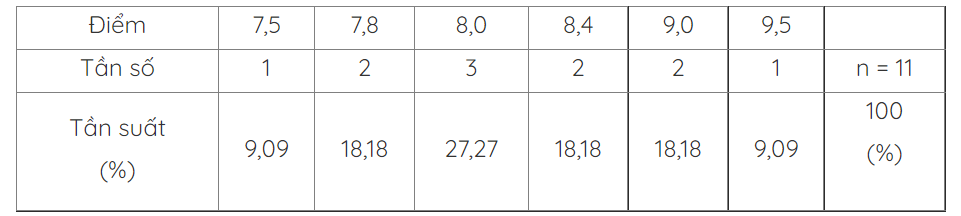
Hãy tính phương sai và độ lệch chuẩn của bảng phân bố tần số, tần suất.
Lời giải:
Điểm trung bình của học sinh là:
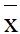 = f1x1 + f2x2 + f3x3 + f4x4 + f5x5 + f6x6
= f1x1 + f2x2 + f3x3 + f4x4 + f5x5 + f6x6
= 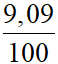 .7,5 +
.7,5 + 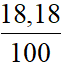 .7,8 +
.7,8 + 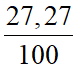 .8,0 +
.8,0 + 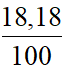 .8,4 +
.8,4 + 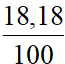 .9,0 +
.9,0 + 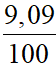 .9,5
.9,5 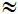 8,3
8,3
Phương sai:
sx2 = f1(x1–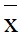 )2 + f2(x2–
)2 + f2(x2–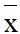 )2 + … + fk(xk–
)2 + … + fk(xk–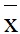 )2
)2
= 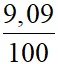 (7,5-8,3)2 +
(7,5-8,3)2 + 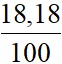 (7,8-8,3)2 +
(7,8-8,3)2 + 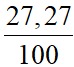 (8,0-8,3)2 +
(8,0-8,3)2 + 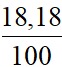 (8,4-8,3)2 +
(8,4-8,3)2 + 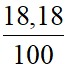 (9,0-8,3)2 +
(9,0-8,3)2 + 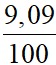 (9,5-8,3)2
(9,5-8,3)2
Độ lệch chuẩn: sx = 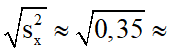 0,59
0,59
Bài 2: Cho bảng phân bố tần số và tần suất ghép lớp sau: Nhiệt độ trung bình của tháng 2 tại thành phố Vinh từ 1961 đến hết 1990 (30 năm)
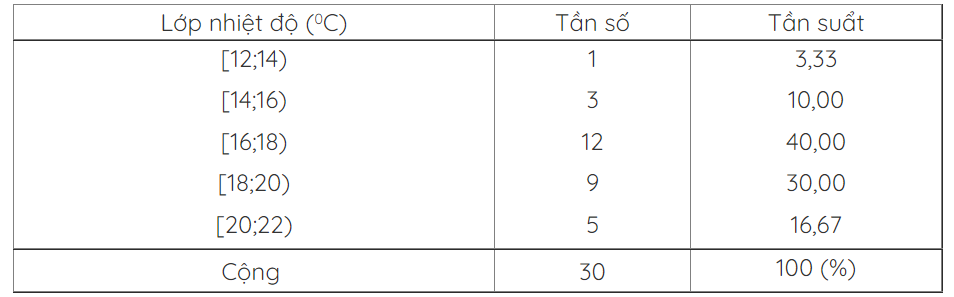
Hãy tính phương sai và độ lệch chuẩn.
Lời giải:
Số trung bình cộng:
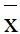 = f1c1 + f2c22 + … + fkck
= f1c1 + f2c22 + … + fkck
= 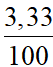 .13 +
.13 + 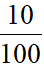 .15 +
.15 + 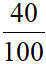 .17 +
.17 + 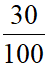 .19 +
.19 + 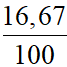 .21
.21
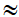 17,93
17,93
Phương sai:
sx2 = f1(c1–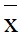 )2 + f2(c2–
)2 + f2(c2–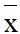 )2 + … + fk(ck–
)2 + … + fk(ck–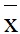 )2
)2
= 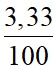 (13-17,93)2 +
(13-17,93)2 + 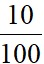 (15-17,93)2 +
(15-17,93)2 + 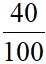 (17-17,93)2 +
(17-17,93)2 + 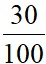 (19-17,93)2 +
(19-17,93)2 + 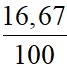 (21-17,93)2
(21-17,93)2
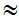 3,93
3,93
Độ lệch chuẩn: sx 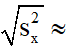 1,98
1,98
Bài 3: Lớp 10C của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được trình bày ở bảng phân bố tần số sau đây:

Hãy tính các số trung bình, phương sai, độ lệch chuẩn.
Lời giải:
Số trung bình:
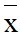 =
= 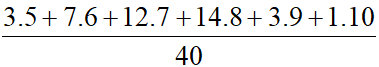 = 7,25
= 7,25
Phương sai:
sx2 = 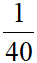 [3.(5-7,25)2 + 7.(6-7,25)2 + 12.(7-7,25)2 + 14.(8-7,25)2 + 3(9-7,25)2 + 1.(10-7,25)2]
[3.(5-7,25)2 + 7.(6-7,25)2 + 12.(7-7,25)2 + 14.(8-7,25)2 + 3(9-7,25)2 + 1.(10-7,25)2]
= 1,2875
Độ lệch chuẩn: sx 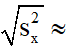 1,135
1,135
D. Bài tập tự luyện.
Bài 1: Lớp 10D của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được trình bày ở bảng phân bố tần số sau đây:

Hãy tính phương sai, độ lệch chuẩn.
Đáp án: sx2 = 0,7875, sx 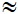 0,8874
0,8874
Bài 2: Cho bảng tần số ghép lớp : Khối lượng của cá mè trong một bể (đơn vị: kg). Hãy tính phương sai, độ lệch chuẩn.

Đáp án: sx2 = 0,042, sx 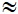 0,2
0,2
Bài 3: Cho bảng tần số ghép lớp : Khối lượng của cá rô phi trong một bể (đơn vị: kg). Hãy tính phương sai, độ lệch chuẩn.

Đáp án: sx2 = 0,064, sx 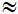 0,253
0,253
Bài 4: Cho bảng tần số ghép lớp : Tuổi thọ của bóng đèn (đơn vị: giờ). Hãy tính phương sai, độ lệch chuẩn.
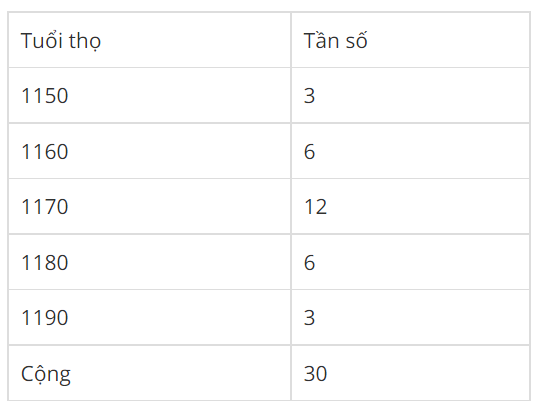
Đáp án: sx2 = 120, sx 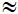 0,95
0,95
Bài 5: Cho bảng tần số ghép lớp : Điểm kiểm tra Toán của học sinh. Hãy tính phương sai, độ lệch chuẩn.
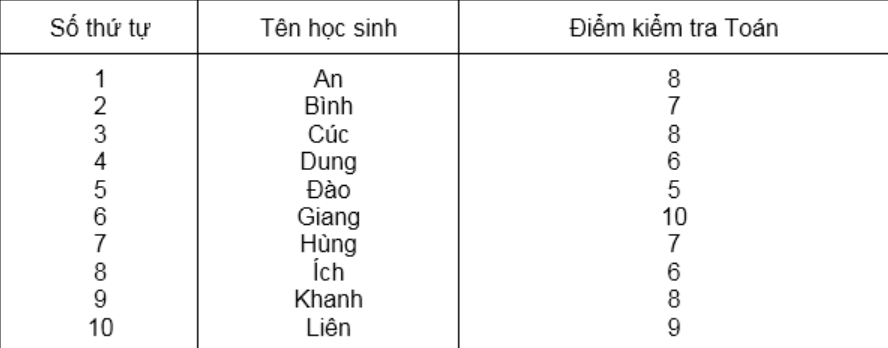
Đáp án: sx2 = 2,04, sx 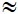 1,43
1,43
Bài 6: Khi điều tra về số cây trồng được của mỗi lớp trong dịp phát động phong trào Tết trồng cây, người ta điều tra và lập được bảng dưới đây:
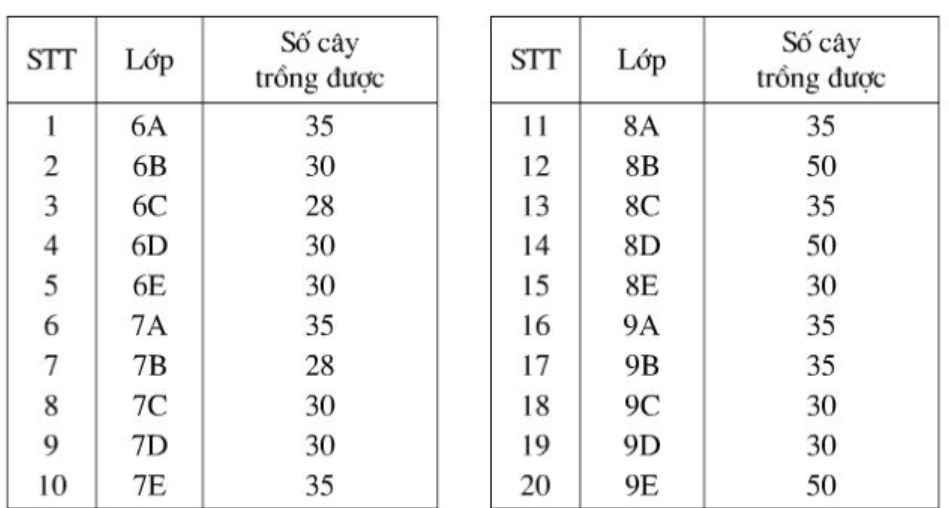
Hãy tính phương sai, độ lệch chuẩn.
Đáp án: sx2 = 48,45, sx 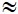 6,96
6,96
Bài 7: Chọn 30 hộp chè mộ cách tùy ý trong kho của một cửa hàng và đem cân, kết quả được ghi lại trong bảng 7 (sau khi đã trừ khối lượng của vỏ):

Hãy tính phương sai, độ lệch chuẩn.
Đáp án: sx2 = 1,067, sx 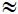 1,033
1,033
Bài 8: Hàng ngày, bạn An thử ghi lại thời gian cần thiết để đi từ nhà đến trường và thực hiện trong 10 ngày, kết quả thu được ghi trong bảng sau (đơn vị: phút). Hãy tính phương sai, độ lệch chuẩn.

Đáp án: sx2 = 1,29, sx 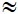 1,136
1,136
Bài tập bổ sung
Bài 1. Cho bảng phân bố tần số và tần suất ghép lớp sau: Nhiệt độ trung bình của tháng 2 tại thành phố Vinh từ 1961 đến hết 1990 (30 năm).
|
Lớp nhiệt độ |
Tần số |
Tần suất |
|
[12;14) |
1 |
3,33 |
|
[14;16) |
3 |
10,00 |
|
[16;18) |
12 |
40,00 |
|
[18;20) |
9 |
30,00 |
|
[20;22) |
5 |
16,67 |
|
Tổng |
30 |
100 (%) |
Hãy tính phương sai và độ lệch chuẩn.
Bài 2. Lớp 10C của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được trình bày ở bảng phân bố tần số sau đây:
|
Điểm thi |
5 |
6 |
7 |
8 |
9 |
10 |
Tổng |
|
Tần số |
3 |
7 |
12 |
14 |
3 |
1 |
40 |
Hãy tính các số trung bình, phương sai, độ lệch chuẩn.
Bài 3. Điểm trung bình các môn học của học sinh được cho trong bảng sau:
|
Điểm |
7,8 |
7,8 |
8,0 |
8,4 |
9,0 |
9,5 |
Tổng |
|
Tần số |
1 |
2 |
3 |
2 |
2 |
1 |
11 |
|
Tần suất (%) |
9,09 |
18,18 |
27,27 |
18,18 |
18,18 |
9,09 |
100 |
Hãy tính phương sai và độ lệch chuẩn của bảng phân bố tần số, tần suất.
Bài 4. Để biết cây đậu phát triển như thế nào sau khi gieo hạt, bạn Châu gieo 5 hạt đậu vào 5 chậu riêng biệt và cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau hai tuần, 5 hạt đậu đã nảy mầm và phát triển thành 5 cây con. Bạn Châu đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị: mi-li-mét) và ghi kết quả là mẫu số liệu sau:
112 102 106 94 101
Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.
Bài 5. Mẫu số liệu về số lượng áo bán ra lần lượt từ tháng 1 đến tháng 12 của một doanh nghiệp là:
430 560 450 550 760 430 525 410 635 450 800 900
Tính độ lệch chuẩn của mẫu số liệu đó.
Xem thêm phương pháp giải các dạng bài tập Toán lớp 10 hay, chi tiết khác:
Lời giải bài tập lớp 10 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn