Cách tìm tâm và bán kính mặt cầu (cực hay) – Tổng hợp các dạng bài tập Toán 12 với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 12.-Cách tìm tâm và bán kính mặt cầu (cực hay)
Cách tìm tâm và bán kính mặt cầu (cực hay)
Bài viết Cách tìm tâm và bán kính mặt cầu với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách tìm tâm và bán kính mặt cầu.
Cách tìm tâm và bán kính mặt cầu (cực hay)
Bài giảng: Cách viết phương trình mặt cầu – dạng bài cơ bản – Cô Nguyễn Phương Anh (Giáo viên VietJack)
+ Phương trình (S): (x-a)2+(y-b)2+(z-c)2=R2 là phương trình mặt cầu (S) có tâm I (a; b; c), bán kính R
+ Phương trình (S): x2+y2+z2-2ax-2by-2cz+d=0 thỏa mãn điều kiện a2+b2+c2-d>0 là phương trình mặt cầu tâm I (a; b; c); bán kính
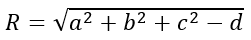
Bài 1: Trong không gian hệ trục tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu, nếu là phương trình mặt cầu, hãy tìm tâm và bán kính của mặt cầu đó
a) (x-2)2+(y+3)2+z2=5
b) x2+y2+z2-2x+4y-6z+1=0
c) 3x2+3y2+3z2-6x+3y+21=0
Lời giải:
a) Phương trình (x-2)2+(y+3)2+z2=5 có dạng
(x-a)2+(y-b)2+(z-c)2=R2 nên là phương trình mặt cầu có tâm
I (2; -3; 0) và bán kính R=√5.
b) Phương trình x2+y2+z2-2x+4y-6z+1=0 có dạng
x2+y2+z2-2ax-2by-2cz+d=0 với a = 1; b = -2; c = 3, d = 1
⇒ a2+b2+c2-d=13>0
Vậy phương trình đã cho là phương trình mặt cầu có tâm I (1; -2; 3) và bán kính R=√13.
c) Phương trình 3x2+3y2+3z2-6x+3y+21=0
⇔ x2+y2+z2-2x+y+7=0
Phương trình có dạng x2+y2+z2-2ax-2by-2cz+d=0 với
a=1;b=(-1)/2;c=0;d=7 ⇒a2+b2+c2-d=(-23)/4<0
Vậy phương trình đã cho không phải là phương trình mặt cầu.
Bài 2: Trong không gian với hệ tọa độ Oxyz, tìm m để mỗi phương trình sau là phương trình mặt cầu.
a) x2+y2+z2-2mx+2(m+1)y-4z+1=0
b) x2+y2+z2-2(m-3)x-4mz+8=0
Lời giải:
a) Phương trình x2+y2+z2-2mx+2(m+1)y-4z+1=0 có
a=m;b=-(m+1); c=2;d=1.
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ m2+(m+1)2+22-1>0⇔2m2+2m+3>0 ⇔m∈R.
b) Phương trình x2+y2+z2-2(m-3)x-4mz+8=0 có a=m-3;
b=0;c=2m;d=8
Phương trình là phương trình mặt cầu ⇔a2+b2+c2-d>0
⇔(m-3)2+4m2-8>0 ⇔5m2-6m+1>0
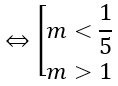
Bài 3: Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 là phương trình của mặt cầu có bán kính nhỏ nhất.
Lời giải:
Phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 có:
a=-(m+2);b=0;c=m-3;d=m2-1
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ (m+2)2+(m-3)2-m2+1>0 ⇔ m2-2m+14>0 ⇔ m∈R.
Khi đó, bán kính mặt cầu là:
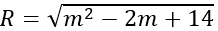
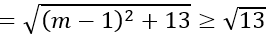
Dấu bằng xảy ra khi m = 1.
Vậy với m = 1 thì mặt cầu có bán kính nhỏ nhất R=√13.
Bài 1: Phương trình nào sau đây là phương trình mặt cầu ?
A. x2+y2+z2-2x=0
B. x2+y2 – z2+2x-y+1=0
C. 2x2+2y2 = (x+y)2 – z2+2x-1
D. (x+y)2 = 2xy – z2 – 1
Lời giải:
Đáp án : A
Giải thích :
Phương trình x2+y2+z2-2ax-2by-2cz+d=0 là phương trình mặt cầu ⇔ a2+b2+c2-d>0
Bài 2: Phương trình nào sau đây không phải là phương trình mặt cầu?
A. x2 + y2 + z2 + 2x – 2y + 1 = 0.
B. x2 + y2 + z2 – 2x = 0.
C. 2x2 + 2y2 = (x + y)2 – z2 + 2x – 1.
D. ( x + y)2 = 2xy – z2 + 1 – 4x.
Lời giải:
Đáp án : C
Giải thích :
Bài 3: Cho các phương trình sau:
( x – 1)2 + y2 + z2 = 1
x2 + ( 2y – 1)2+ z2 = 4
x2 + y2 + z2 + 1 = 0
( 2x + 1)2+ ( 2y – 1)2 + 4z2 = 16
Số phương trình là phương trình mặt cầu là:
A. 1 B. 3
C. 4 D. 2
Lời giải:
Đáp án : D
Giải thích :
Các phương trình mặt cầu là:
( x – 1)2 + y2 + z2 = 1
x2 + ( 2y – 1)2 + z2 = 4
Bài 4: Mặt cầu ( S ): x2+ y2+ z2– 2x + 10y + 3z + 1 = 0 đi qua điểm có tọa độ nào sau đây?
A. (3; – 2; – 4) B. ( 2;1;9)
C. ( 4; – 1;0) D.(- 1;3; – 1)
Lời giải:
Đáp án : B
Giải thích :
Thử trực tiếp đáp án, điểm (2; 1; 9) thỏa mãn phương trình mặt cầu.
Bài 5: Mặt cầu ( S ): x2+ y2 + z2 – 4x + 1 = 0 có tọa độ tâm và bán kính R là:
A. I(-2;0;0), R = √3
B. I(2;0;0), R = √3
C. I(0;2;0), R = √3
D. I(2;0;0), R = 3
Lời giải:
Đáp án : B
Giải thích :
( S ): x2 + y2 + z2– 4x + 1 = 0
⇔ (x-2)2+y2+z2=3
Phương trình có tâm I (2 ; 0 ; 0), bán kính R=√3
Bài 6: Phương trình mặt cầu có tâm I(-1;2;3), bán kình R=3 là:
A. (x + 1)2+ ( y – 2)2 + ( z + 3)2 = 9
B. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 3
C. ( x – 1)2+ ( y + 2)2 + ( z – 3)2 = 9
D. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 9
Lời giải:
Đáp án : A
Giải thích :
Phương trình mặt cầu tâm I (a; b; c), bán kính R là:
(x-a)2+(y-b)2+(z-c)2=R2
Bài 7: Mặt cầu ( S ): ( x + y)2= 2xy – z2 + 1 – 4x có tâm là:
A. I(2;0;0) B. I(4;0;0)
C. I(-4;0;0) D. I(-2;0;0)
Lời giải:
Đáp án : D
Giải thích :
(x+y)2=2xy-z2+1-4x ⇔ x2+y2+z2+4x=1
Phương trình có a=-2;b=0;c=0 ⇒ I(-2;0;0)
Bài 8: Mặt cầu có phương trình nào sau đây có tâm là I(-1;1;0) ?
A. x2+ y2 + z2+ 2x – 2y + 1 = 0.
B. x2 + y2+ z2 – 2x + 2y = 0.
C. 2x2 + 2y2 = ( x + y)2 – z2+ 2x – 1 – 2xy.
D. ( x + y)2 = 2xy – z2+ 1 – 4x.
Lời giải:
Đáp án : A
Giải thích :
A. x2+ y2 + z2 + 2x – 2y + 1 = 0.
⇔ (x+1)2+(y-1)2+z2=1
Phương trình có tâm I (-1 ; 1 ; 0), bán kính R =1
B. x2 + y2 + z2 – 2x + 2y = 0.
⇔ (x-1)2+(y+1)2+z2=2
Phương trình có tâm I (1 ; -1 ; 0), bán kính R=√2
C.2x2+ 2y2= ( x + y )2 – z2 + 2x – 1 – 2xy.
⇔ x2+y2+z2-2x+1=0
⇔ (x-1)2+y2+z2=0
Đây không phải là phương trình mặt cầu.
D. (x + y)2= 2xy – z2+ 1 – 4x.
⇔ x2+y2+z2+4x-1=0
⇔(x+2)2+y2+z2=5
Phương trình có tâm I (-2 ; 0 ; 0), bán kính R=√5
Bài 9: Gọi I là tâm mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4. Độ dài OI→ (O là gốc tọa độ) bằng?
A. 1 B. 4
C. 2 D. √2
Lời giải:
Đáp án : C
Giải thích :
Mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4 có tâm I (0; 0; 2) ⇒ OI=2
Bài 10: Phương trình mặt cầu có bán kính bằng 3 và tâm là giao điểm của ba trục toạ độ ?
A. x2+ y2 + z2 – 6x = 0.
B. x2 + y2 + z2 – 6y = 0.
C. x2 + y2 + z2 – 6z = 0.
D. x2 + y2 + z2 = 9.
Lời giải:
Đáp án : D
Giải thích :
Giao điểm của 3 trục tọa độ là điểm O (0; 0; 0)
Khi đó, phương trình mặt cầu có tâm O (0; 0; 0) và bán kính R = 3 là
x2+y2+z2=9
Bài 1. Cho mặt cầu (S): x2 + y2 + z2 – 2x + 10y + 3z + 1 = 0, tìm tâm và bán kính mặt cầu.
Bài 2. Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2 + y2 + z2 + 2(m + 2)x – 2(m – 3)z + m2 – 1 = 0 là phương trình của mặt cầu có bán kính nhỏ nhất.
Bài 3. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x + 1)2 + (y – 2)2 + (z – 1)2 = 9. Tìm tọa độ tâm I và tính bán kính R của (S).
Bài 4. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x + 1)2 + (y + 3)2 + z2 = 9. Tìm tọa độ tâm I và tính bán kính R của (S).
Bài 5. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): x2 + y2 – 2x + 4y – 2z = 19. Tìm tọa độ tâm O và tính bán kính R của (S).
Bài giảng: Cách viết phương trình mặt cầu – dạng bài nâng cao – Cô Nguyễn Phương Anh (Giáo viên VietJack)

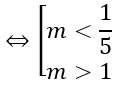

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn