Công thức, cách tính độ dài đường trung tuyến (cực hay, chi tiết) – Tổng hợp các dạng bài tập Toán 10 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 10.-Công thức, cách tính độ dài đường trung tuyến (cực hay, chi tiết)
Công thức, cách tính độ dài đường trung tuyến (cực hay, chi tiết)
Bài viết Công thức, cách tính độ dài đường trung tuyến với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Công thức, cách tính độ dài đường trung tuyến.
Công thức, cách tính độ dài đường trung tuyến (cực hay, chi tiết)
Áp dụng công thức tính độ dài đường trung tuyến:
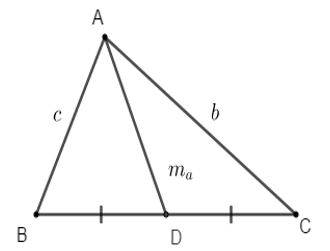
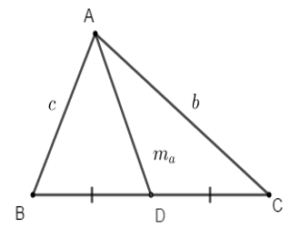
Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi ma; mb; mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác. Khi đó
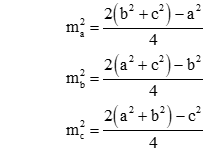
Ví dụ 1: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài các đường trung tuyến của tam giác ABC.
Hướng dẫn giải:
Gọi độ dài trung tuyến từ các đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc.
Áp dụng công thức trung tuyến ta có:
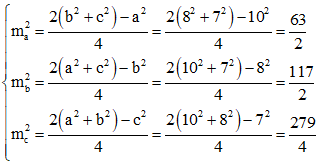
Vì độ dài các đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:
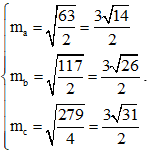
Ví dụ 2: Cho tam giác ABC, có BC = a, CA = b và AB = c. Chứng minh rằng nếu b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau.
Hướng dẫn giải:
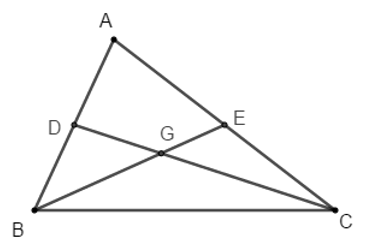
Gọi D và E lần lượt là trung điểm của AB và AC, G là trọng tâm tam giác ABC.
Đặt BE = mb, CD = mc
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
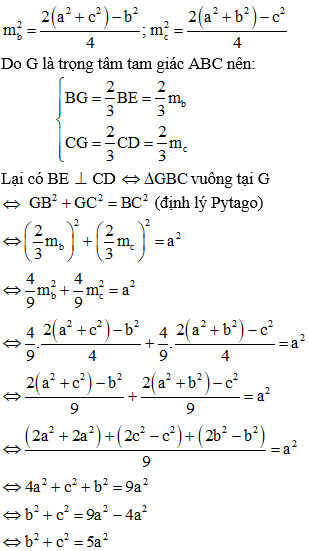
Vậy b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau. (đpcm)
Ví dụ 3: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến 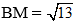 . Độ dài AC là:
. Độ dài AC là:
Hướng dẫn giải:
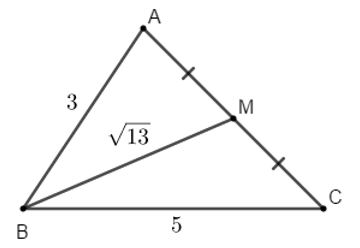
BM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có:
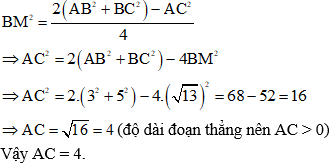
Đáp án B
Ví dụ 4: Tam giác ABC có BC = 6, AC = 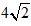 , AB = 2. M là một điểm trên cạnh BC sao cho BM = 3. Giá trị của AM là?
, AB = 2. M là một điểm trên cạnh BC sao cho BM = 3. Giá trị của AM là?
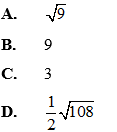
Hướng dẫn giải:
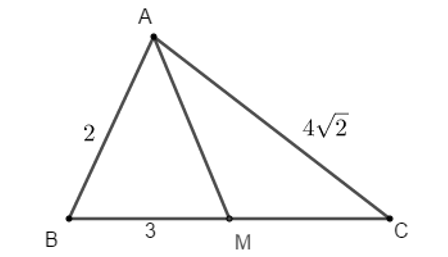
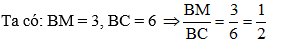
Mà M thuộc BC.
Do đó M là trung điểm của BC => AM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có.
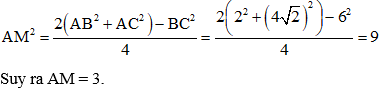
Đáp án C
Ví dụ 5: Gọi S = ma2 + mb2 + mc2 là tổng bình phương độ dài ba đường trung tuyến của tam giác ABC. Khẳng định nào sau đây là đúng? (cho BC = a, CA = b, AB = c)
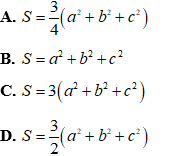
Hướng dẫn giải:
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
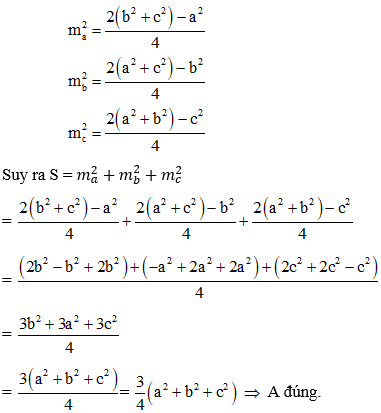
Đáp án A
Bài 1. Tam giác ABC có AB = AC = 10 cm, BC = 12 cm. Tính độ dài đường trung tuyến AM.
Hướng dẫn giải:
Ta có tam giác ABC cân tại A, AM là trung tuyến suy ra AM là đường cao, đường phân giác của tam giác ABC nên BM = MC = 12BC = 6 cm
Áp dụng định lý Pythagore cho tam giác vuông AMC có:
AC2 = AM2 + MC2 ⇒AM=AC2-MC2 = 8 cm
Bài 2. Tính độ dài đường trung tuyến AM của tam giác ABC có góc BAC^=120°, AB = 4 cm, AC = 6 cm
Hướng dẫn giải:
Ta có BC2 = AB2 + AC2 – 2.AB.AC.cos120o
⇒BC=29
⇒AM2=AB2+AC22-BC24
⇒AM=7
Bài 3. Cho tam giác ABC vuông tại A có độ dài hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm. Tính độ dài cạnh AB.
Hướng dẫn giải:
Tam giác ABC vuông tại A, AM là trung tuyến nên AM = BM = MC = 6
Suy ra BC = 12
Mặt khác:
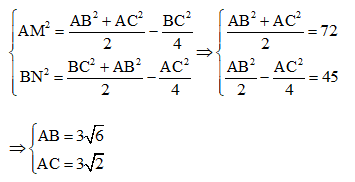
Bài 4. Cho tam giác ABC cân ở A có AB = AC = 17 cm, BC= 16 cm. Kẻ trung tuyến AM.
a) Chứng minh: AM ⊥ BC;
b) Tính độ dài AM.
Hướng dẫn giải:
a. Ta có AM là đường trung tuyến tam giác ABC nên MB = MC
Mặt khác tam giác ABC là tam giác cân tại A
Suy ra AM vừa là đường trung tuyến vừa là đường cao
Vậy AM vuông góc với BC
b. Ta có
BC = 16cm nên BM = MC = 8cm
AB = AC = 17cm
Xét tam giác AMC vuông tại M
Áp dụng định lý Pythagore ta có: AC2 = AM2 + MC2 hay 172 = AM2 + 82.
Suy ra AM2 = 172 – 82 = 225.
Do đó AM = 15 cm.
Bài 5. Cho tam giác MNP cân ở M có MB = MC = 17 cm, NP= 16 cm. Kẻ trung tuyến MI.
a) Chứng minh: MI ⊥ NP;
b) Tính độ dài MI.
Hướng dẫn giải:
a) Do MI là đường trung tuyến MNP nên IP = IN.
Mặt khác tam giác MNP cân tại M.
Do đó MI vừa là đường trung tuyến vừa là đường cao hay MI ⊥ NP.
b) Ta có:
• NP = 16 cm nên NI = PI = 8 cm.
• MN = MP = 17 cm.
Xét tam giác MIP vuông tại I
Áp dụng định lý Pythagore, ta có:
• MP2 = MI2 + IP2 hay 192 = MI2 + 82
• MI2 = 172 – 82 = 225 suy ra MI = 15 cm.
Bài 6. Tam giác MNP cho biết NP = 20 cm, PM = 16 cm, MN = 14 cm. Tính độ dài các đường trung tuyến của tam giác MNP.
Bài 7. Cho tam giác ABC có a = 6 cm, b = 8 cm, c = 10 cm. Tính độ dài các đường trung tuyến của tam giác ABC.
Bài 8. Cho tam giác ABC vuông tại B có độ dài hai đường trung tuyến BM và CN lần lượt bằng 5 cm và 7 cm. Tính độ dài cạnh BC.
Bài 9. Tính độ dài đường trung tuyến BM của tam giác ABC có góc ABC^=120°, BC = 5 cm, AB = 10 cm.
Bài 10. Cho tam giác ABC có AB = 6, BC = 10 và độ dài đường trung tuyến BM = 19. Tính độ dài AC.
Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:
Lời giải bài tập lớp 10 sách mới:

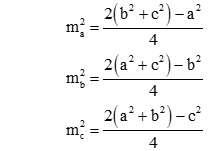
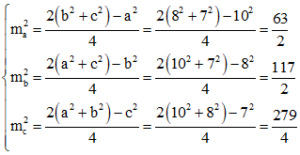

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn