Công thức, cách tính Diện tích tam giác (cực hay, chi tiết) – Tổng hợp các dạng bài tập Toán 10 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 10.-Công thức, cách tính Diện tích tam giác (cực hay, chi tiết)
Công thức, cách tính Diện tích tam giác (cực hay, chi tiết)
Bài viết Công thức, cách tính Diện tích tam giác với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Công thức, cách tính Diện tích tam giác.
Công thức, cách tính Diện tích tam giác (cực hay, chi tiết)
1. Phương pháp giải
Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức dưới đây.
Cho tam giác ABC có BC = a, CA = b và AB = c, gọi ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;

2. Bài tập tự luyện
Ví dụ minh họa hoặc bài tập có giải
Ví dụ 1: Cho tam giác ABC có AC = 3, AB = 5, cosA = 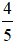 .
.
a, Tính diện tích tam giác ABC.
b, Tính đường cao ha của tam giác ABC.
Hướng dẫn giải:
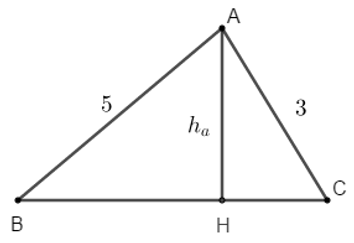
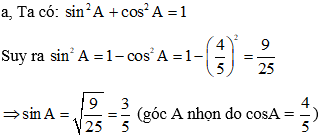
Áp dụng công thức tính diện tích tam giác, ta có diện tích tam giác ABC là:
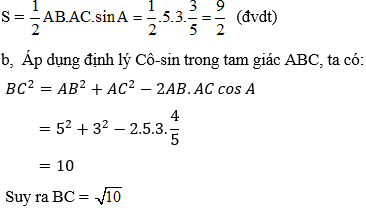
Áp dụng công thức tính diện tích tam giác ABC ta lại có:
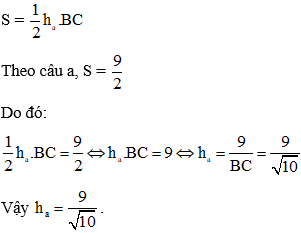
Ví dụ 2: Cho tam giác ABC có 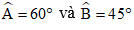 và cạnh AC = 4. Tính các cạnh còn lại, diện tích tam giác ABC và đường cao hạ từ đỉnh B.
và cạnh AC = 4. Tính các cạnh còn lại, diện tích tam giác ABC và đường cao hạ từ đỉnh B.
Hướng dẫn giải:
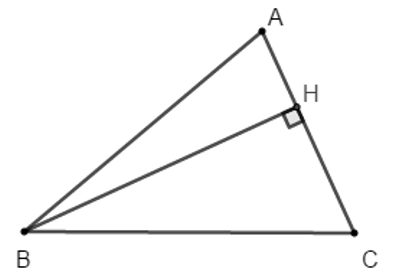

Ví dụ 3: Cho tam giác ABC ngoại tiếp đường tròn tâm O, bán kính r = 5cm. Tính diện tích tam giác ABC biết các cạnh BC = 7cm, CA = 8cm, AB = 10cm.
Hướng dẫn giải:
+ Nửa chu vi tam giác ABC là: 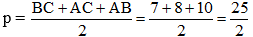
+ Tam giác ABC ngoại tiếp đường tròn tâm O bán kính r = 5cm, nên r là bán kính đường tròn nội tiếp tam giác ABC, áp dụng công thức tính diện tích, ta có diện tích tam giác ABC là:
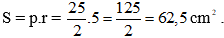
Ví dụ 4: Cho tam giác ABC có các đỉnh A(1; -2), B(-2; 3), C(0; 4). Tính diện tích tam giác ABC.

Hướng dẫn giải:
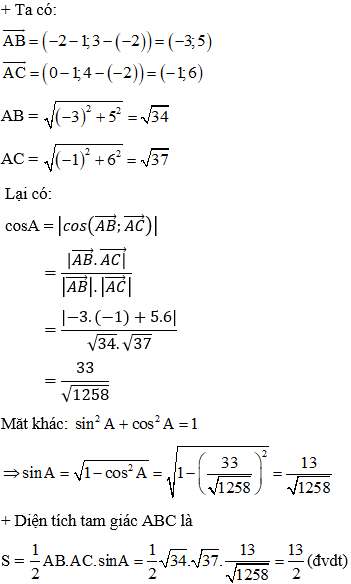
Đáp án A
Ví dụ 5: Cho tam giác ABC vuông tại A có AC = 15 và AB = 8. Diện tích, chu vi và đường cao hạ từ A của tam giác ABC lần lượt là.

Hướng dẫn giải:
+ Tam giác ABC vuông tại A
Do đó diện tích tam giác ABC là: 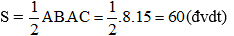
+ Ta có: BC2 = AB2 + AC2 (theo định lý Pytago trong tam giác vuông ABC)
Suy ra: 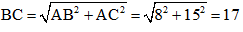
Chu vi tam giác ABC là: C = AB + AC + BC = 8 + 15 + 17 = 40
+ Lại có diện tích tam giác ABC là
S = 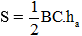 (với ha là độ dài đường cao hạ từ A)
(với ha là độ dài đường cao hạ từ A)
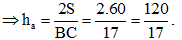
Đáp án B
Bài tập tự luyện
Bài 1. Tam giác ABC có AB = 2, AC = 5, BAC^=60°. Tính diện tích tam giác ABC.
Bài 2. Tam giác ABC có AB = 21, AC = 17, BC = 10. Tính diện tích của tam giác ABC.
Bài 3. Tính diện tích tam giác đều nội tiếp đường tròn bán kính R = 6 cm.
Bài 4. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C. Tính diện tích của tam giác mới được tạo thành.
Bài 5. Tam giác ABC có BC = a và AC = b. Tìm giá trị góc C để diện tích tam giác ABC là lớn nhất.
Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:
Lời giải bài tập lớp 10 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn