Bài 2.6 trang 58 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12 – Tuyển chọn giải Toán 12 Kết nối tri thức Tập 1, Tập 2 hay, chi tiết giúp bạn làm bài tập Toán 12.-Bài 2.6 trang 58 Toán 12 Kết nối tri thức Tập 1
Bài 2.6 trang 58 Toán 12 Kết nối tri thức Tập 1
Giải Toán 12 Bài 6: Vectơ trong không gian – Kết nối tri thức
Bài 2.6 trang 58 Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu SA→+SC→=SB→+SD→.
Lời giải:
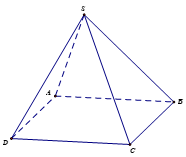
Chứng minh: Nếu ABCD là hình bình hành thì SA→+SC→=SB→+SD→ .
Vì ABCD là hình bình hành nên
AD→=BC→ ⇔SD→−SA→=SC→−SB→⇔SA→+SC→=SB→+SD→.
Chứng minh: Nếu SA→+SC→=SB→+SD→ thì ABCD là hình bình hành.
Có SA→+SC→=SB→+SD→ ⇔SA→−SD→=SB→−SC→⇔DA→=CB→ .
Suy ra ABCD là hình bình hành.
Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 12 hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn