Các dạng bài tập Nguyên hàm chọn lọc, có đáp án

---

---

Phần Nguyên hàm Toán lớp 12 với các dạng bài tập chọn lọc có trong Đề thi THPT Quốc gia và trên 200 bài tập trắc nghiệm chọn lọc, có đáp án. Vào Xem chi tiết để theo dõi các dạng bài Nguyên hàm hay nhất tương ứng.

Các dạng bài tập Nguyên hàm chọn lọc, có đáp án

Bài giảng: Cách làm bài tập nguyên hàm và phương pháp tìm nguyên hàm của hàm số cực nhanh – Cô Nguyễn Phương Anh (Giáo viên VietJack)

Cách tìm nguyên hàm của hàm số

I. NGUYÊN HÀM VÀ TÍNH CHẤT

1. Nguyên hàm

Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.

Định lí:

    1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

    2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó F(x)+C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C.

2. Tính chất của nguyên hàm

        Tính chất 1: (∫f(x)dx)’ = f(x) và ∫f'(x)dx = f(x) + C

        Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.

        Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx

3. Sự tồn tại của nguyên hàm

        Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Bảng nguyên hàm của một số hàm số sơ cấp

Nguyên hàm của hàm số sơ cấp	Nguyên hàm của hàm số hợp (u = u(x)

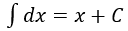
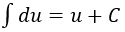
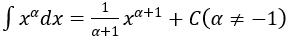
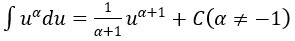
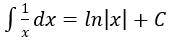
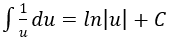
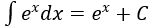
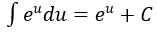
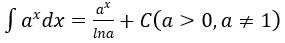
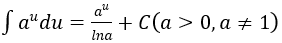
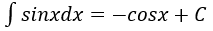
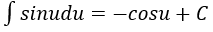
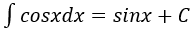
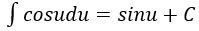
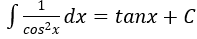
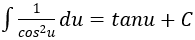
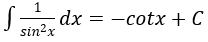
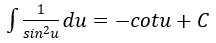
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM

Phương pháp dùng định nghĩa vá tính chất

    + Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x.

    + Đưa các mỗi biểu thức chứa x về dạng cơ bản có trong bảng nguyên hàm.

    + Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản.

Bài 1: Tìm nguyên hàm của hàm số

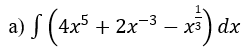
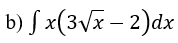
Lời giải:

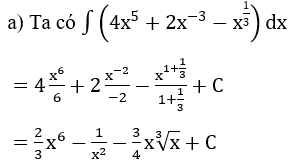
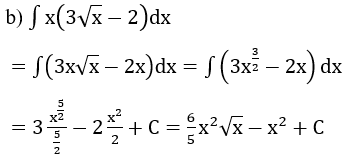
Bài 2: Tìm nguyên hàm của hàm số

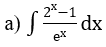
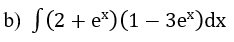
Lời giải:

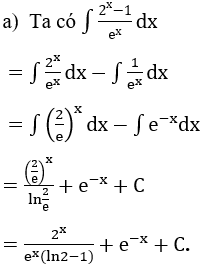
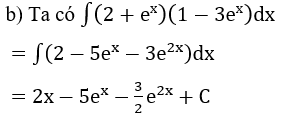
Tìm nguyên hàm bằng phương pháp đổi biến số

STT	Dạng tích phân	Cách đặt	Đặc điểm nhận dạng
1		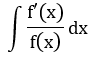t = f(x)	Biểu thức dưới mẫu
2		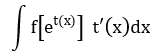t = t(x)	Biểu thức ở phần số mũ
3		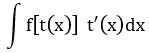t = t(x)	Biểu thức trong dấu ngoặc
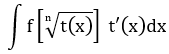
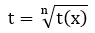
4			Căn thức
5		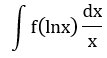t = lnx	dx/x đi kèm biểu thức theo lnx
6		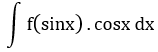t = sinx	cosx dx đi kèm biểu thức theo sinx
7		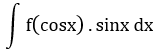t = cosx	sinx dx đi kèm biểu thức theo cosx
8		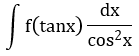t = tanx	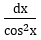đi kèm biểu thức theo tanx
9		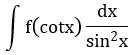t = cotx	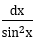đi kèm biểu thức theo cotx
10		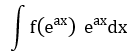t = eax	eax dx đi kèm biểu thức theo eax
Đôi khi thay cách đặt t = t(x) bởi t = m.t(x) + n ta sẽ biến đổi dễ dàng hơn.

Bài 1: Tìm các họ nguyên hàm sau đây:

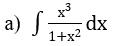
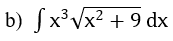
Lời giải:

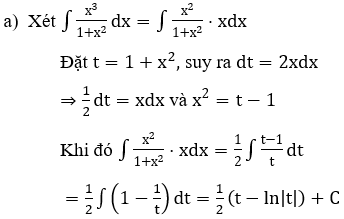
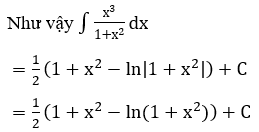
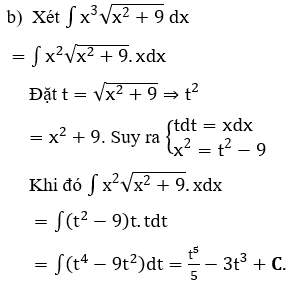
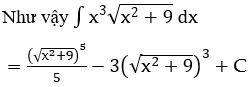
Bài 2: Tìm các họ nguyên hàm sau đây:

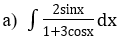
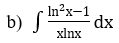
Lời giải:

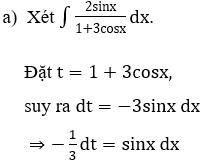
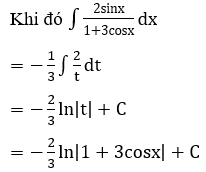
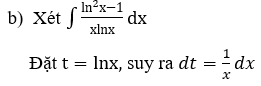
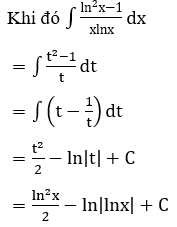
Bài 3: Tìm các họ nguyên hàm sau đây:

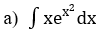
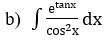
Lời giải:

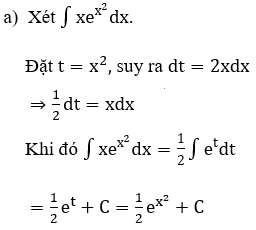
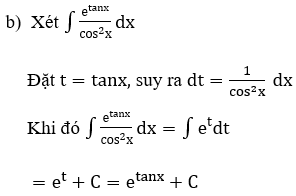
Cách tìm nguyên hàm bằng phương pháp từng phần

Với bài toán tìm nguyên hàm của các hàm số dạng tích (hoặc thương) của hai hàm số “khác lớp hàm” ta thường sử dụng phương pháp nguyên hàm từng phần theo công thức

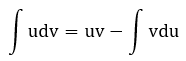
Dưới đây là một số trường hợp thường gặp như thế (với P(x) là một đa thức theo ẩn x)

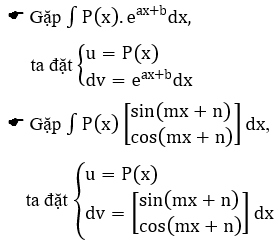
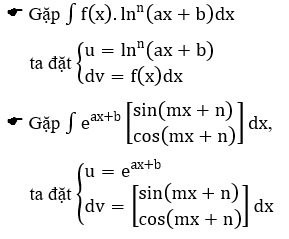
Bài 1: Tìm họ nguyên hàm của hàm số

a) ∫xsinxdx

b) ∫e^x sinx dx

Lời giải:

a) Xét ∫xsinxdx

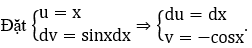
Theo công thức tính nguyên hàm từng phần, ta có

F(x) = ∫xsinxdx = -xcosx+∫cosxdx = -xcosx+sinx+C

b) Xét F(x) = ∫e^x sinx dx

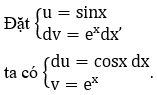
F(x) = e^x sinx-∫e^x cosx dx = e^x sinx-G(x) (1)

Với G(x) = ∫e^x cosx dx

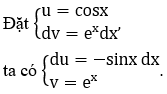
G(x) = e^x cosx+∫e^x sinx dx+C’=e^x cosx+F(x)+C’ (2)

Từ (1) và (2) ta có F(x) = e^x sinx-e^x cosx – F(x) – C’

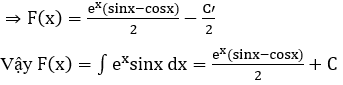
Ghi nhớ: Gặp ∫e^mx+n.sin(ax+b)dx hoặc ∫e^mx+n.cos(ax+b)dx ta luôn thực hiện phương pháp nguyên hàm từng phần 2 lần liên tiếp.

Bài 2: Tìm họ nguyên hàm của hàm số

a) ∫x.2^x dx

b) ∫(x²-1) e^x dx

Lời giải:

a) Xét ∫x.2^x dx

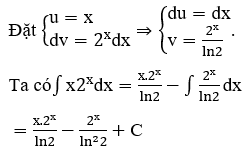
b)

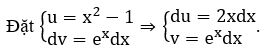
Suy ra ∫f(x)dx = (x²-1) e^x – ∫2x.e^x dx

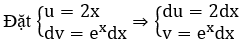
Suy ra ∫f(x)dx = (x²-1) e^x – ∫2x.e^x dx = (x²-1) e^x-(2x.e^x – ∫2.e^x dx)

= (x²-1) e^x – 2x.e^x + 2.e^x+C = (x-1)² e^x + C.

Bài 3: Tìm họ nguyên hàm của hàm số

a) ∫2xln(x-1)dx

b)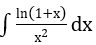

Lời giải:

a) Xét ∫2xln(x-1)dx

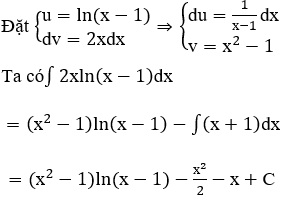
b)

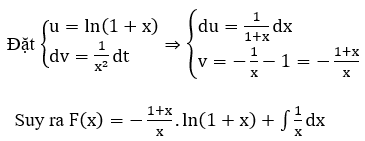
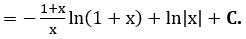
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:

---

---

---