Nội dung bài viết
Các phương pháp tính thể tích hình chóp, khối chóp (cực hay) – Tổng hợp các dạng bài tập Toán 12 với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 12.-Các phương pháp tính thể tích hình chóp, khối chóp (cực hay)
Các phương pháp tính thể tích hình chóp, khối chóp (cực hay)
Dưới đây là các phương pháp, các cách tính Thể tích hình chóp, khối chóp cực hay với phương pháp giải và nhiều ví dụ, bài tập minh họa có lời giải.
Các phương pháp tính thể tích hình chóp, khối chóp (cực hay)
Bài giảng: Cách tính Thể tích hình chóp, hình lăng trụ – Cô Nguyễn Phương Anh (Giáo viên Meraki Center)
Công thức tính thể tích khối chóp
* Nếu khối chóp đã cho có chiều cao h và diện tích đáy Sday thì thể tích tính theo công thức:
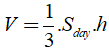
* Để xác định được chiều cao của hình chóp ta cần xác định:
• Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
• Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
• Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.
• Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
• Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt đáy thuộc cạnh mặt đáy đường cao là từ đỉnh tới hình chiếu.
Chú ý: Các công thức tính diện tích đa giác
a) Tam giác:
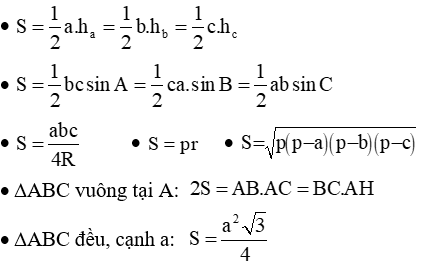
b) Hình vuông cạnh a: S = a2(a: cạnh hình vuông)
c) Hình chữ nhật: S = a.b (a, b: hai kích thước)
d) Hình bình hành ABCD: S = đáy x cao = AB. AD.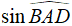
e) Hình thoi ABCD: S= AB. AD.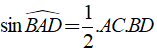
f) Hình thang: 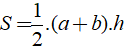 (a,b: hai đáy, h: chiều cao)
(a,b: hai đáy, h: chiều cao)
g) Tứ giác ABCD có hai đường chéo vuông góc: 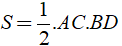
Tính thể tích khối chóp có cạnh bên vuông góc với đáy
Chú ý khi giải toán
+ Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.
+ Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, AC=a√2, SA vuông góc với mặt phẳng (ABC), SA = a. Tính thể tích khối chóp S.ABC
Lời giải:
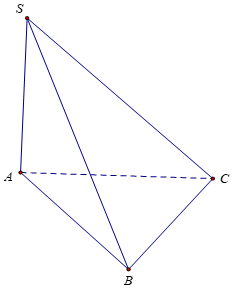
ABC là tam giác vuông cân ở B, AC=a√2 nên
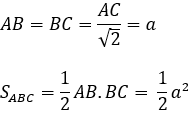
SA vuông góc với mặt phẳng ABC nên SA là đường cao
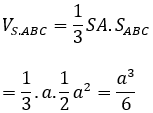
Bài 2: Cho khối chóp S.ABC có SA vuông góc với đáy, SA = 4; AB = 6; BC = 10 và CA = 8. Tính thể tích V của khối chóp S.ABC
Lời giải:
Nửa chu vi của tam giác là: p = 12
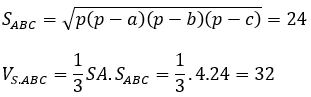
Bài 3: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. SA vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 30º.Tính theo a thể tích của khối chóp S.ABC
Lời giải:
Do SA ⊥ (ABC) nên AB là hình chiếu vuông góc của SB lên mặt phẳng (ABC).
⇒ Góc giữa đường thẳng SB và mặt phẳng (ABC) là 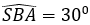
Xét tam giác SAB vuông tại A có:
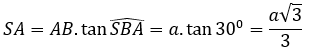
∆ABC đều cạnh a nên
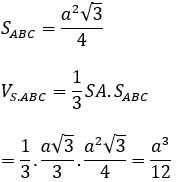
Bài 4: Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = 2a, AD = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa SC và mặt phẳng S.ABCD bằng 60º. Tính theo a thể tích khối chóp S.ABCD
Lời giải:
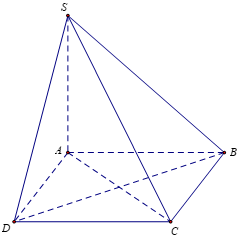
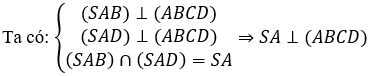
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)
Do đó, góc giữa SC và mặt phẳng (ABCD) là 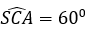
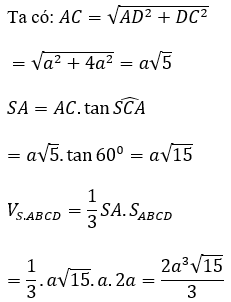
Bài 5: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy và AB = a, AC = 2a, góc BAC = 120º. Mặt phẳng (SBC) tạo với đáy một góc 60º. Tính theo a thể tích khối chóp S.ABC
Lời giải:
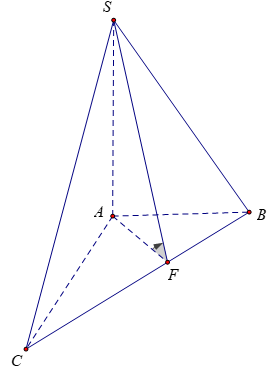
Gọi F là hình chiếu vuông góc của A lên BC.
(SBC) ∩ (ABC) = BC
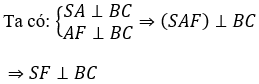
Vậy góc giữa (SBC) và (ABC) là góc SFA = 60º
Xét tam giác ABC, AB = a, AC = 2a, góc BAC = 120º có:
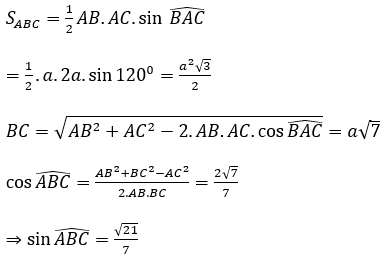
Xét tam giác ABF vuông tại F có:
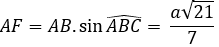
Xét tam giác ABF vuông tại F có:
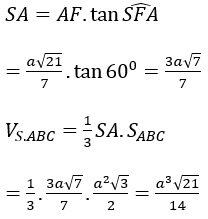
Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là một đa giác đều và các cạnh bên bằng nhau.
2. Kết quả: Trong hình chóp đều:
+ Đường cao hình chóp qua tâm của đa giác đáy.
+ Các cạnh bên tạo với đáy các góc bằng nhau.
+ Cắt mặt bên tạo với đáy các góc bằng nhau.
Bài 1: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5
Lời giải:
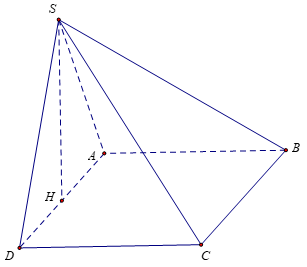
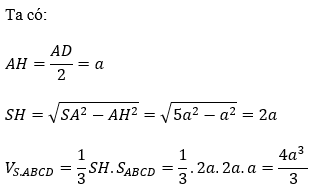
Bài 2: Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB = 3a, AC = 6a. Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH = 2HB. Biết SC hợp với (ABC) một góc bằng 60º . Tính thể tích khối chóp S.ABC
Lời giải:
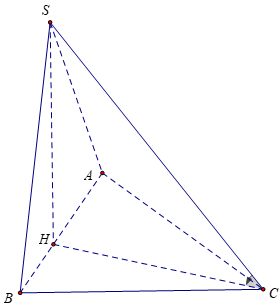
Tam giác ABC vuông tại B, AB = 3a, AC = 6a
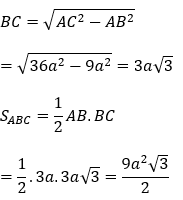
AH = 2HB; AB = 3a ⇒ HB = a
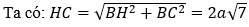
Có: SH⊥(ABCD) nên góc giữa SC và (ABC) là góc giữa SC và HC
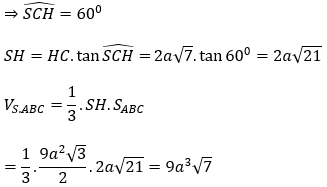
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, BC=a√3, H là trung điểm của cạnh AD. Biết hai mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt đáy, đường thẳng SD tạo với đáy một góc 60º . Tính thể tích của khối chóp theo a
Lời giải:
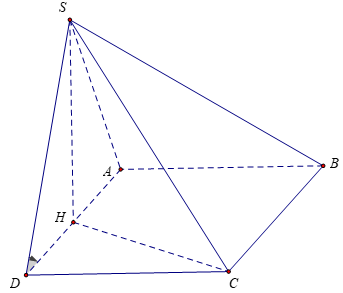
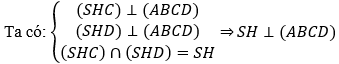
HD là hình chiếu vuông góc của SD lên mặt phẳng (ABCD). Do đó góc giữa đường thẳng SD và đáy là góc giữa HD và SD
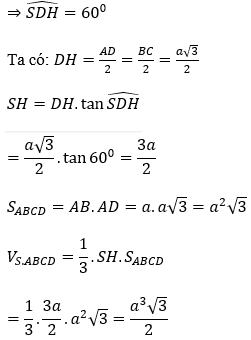
Bài 4: Cho khối chóp đều S.ABCD có cạnh đáy bằng a√3. Tính thể tích khối chóp S.ABCD biết góc giữa cạnh bên và mặt đáy bằng 60°.
Lời giải:
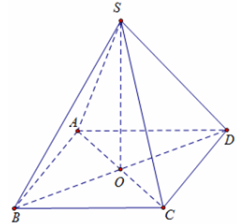
Gọi O là tâm của hình vuông ABCD khi đó SO⊥(ABCD)
suy ra góc SDO =(SD,(ABCD))=60º .
Lại có đáy ABCD là hình vuông cạnh a√3
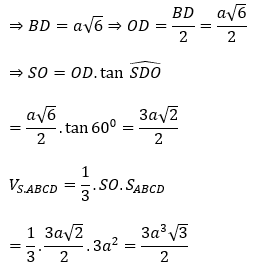
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:



Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn