Các trường hợp đồng dạng của tam giác đầy đủ, chi tiết – Tổng hợp Lý thuyết Toán 8 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 8.-Các trường hợp đồng dạng của tam giác đầy đủ, chi tiết
Các trường hợp đồng dạng của tam giác đầy đủ, chi tiết
Bài viết Các trường hợp đồng dạng của tam giác lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Các trường hợp đồng dạng của tam giác.
Các trường hợp đồng dạng của tam giác
Bài giảng: Bài 5: Trường hợp đồng dạng thứ nhất – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
1. Trường hợp đồng dạng thứ nhất: Góc – Góc
a) Định nghĩa
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
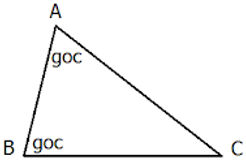
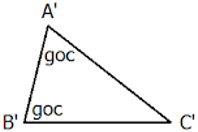
Tổng quát: Δ ABC ∼ Δ A’B’C’ ⇔ 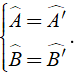
b) Ví dụ áp dụng
Ví dụ: Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
Lời giải:
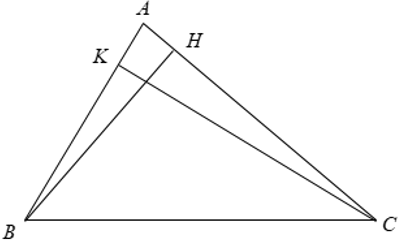
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g – g )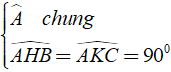
2. Trường hợp đồng dạng thứ hai: Cạnh – Cạnh – Cạnh
a) Định nghĩa
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
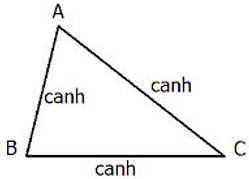
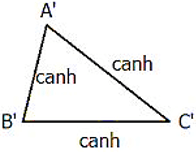
Tổng quát: Δ ABC,Δ A’B’C’ có A’B’/AB = A’C’/AC = B’C’/BC ⇒ Δ ABC ∼ Δ A’B’C’
b) Ví dụ áp dụng
Ví dụ: Cho Δ ABC,Δ A’B’C’ có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A’B’C’
Lời giải:
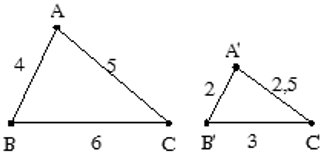
Xét Δ ABC,Δ A’B’C’ có A’B’/AB = A’C’/AC = B’C’/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A’B’C’ ( c – c – c )
3. Trường hợp đồng dạng thứ ba: Cạnh – Góc – Cạnh
a) Định nghĩa
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng
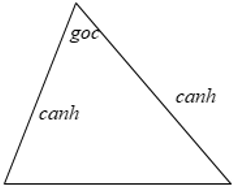
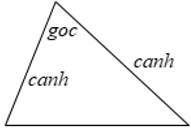
Tổng quát: Δ ABC,Δ A’B’C’ có A’B’/AB = A’C’/AC và Aˆ = A’ˆ
⇒ Δ ABC ∼ Δ A’B’C’ ( c – g – c )
b) Ví dụ áp dụng
Ví dụ: Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Lời giải:
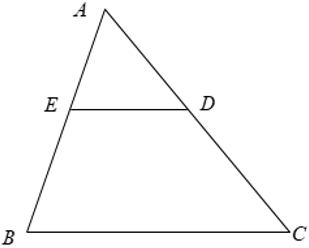
Xét Δ AED và Δ ABC có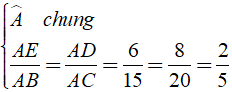
⇒ Δ AED ∼ Δ ABC ( c – g – c )
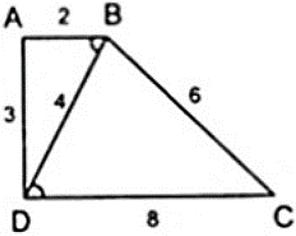
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Lời giải:
a) Ta có:
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c – c – c )
b) Ta có: Δ BAD ∼ Δ DBC
⇒ ABDˆ = BDCˆ nên AB//CD
⇒ ABCD là hình thang.
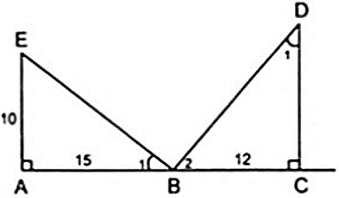
Bài 2: Cho hình vẽ như bên, biết EBAˆ = BDCˆ
a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.
b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)
c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD
Lời giải:
a) Từ giả thiết và tính chất về góc của tam giác vuông BCD ta có: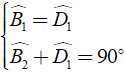
⇒ Bˆ1 + Bˆ2 = 900 ⇒ EBDˆ = 900 , do ABCˆ là góc bẹt
Vậy trong hình vẽ có 3 tam giác vuông là ABE, BCD, EDB
b) Ta có: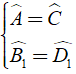
⇒ Δ CDB ∼ Δ ABE ( g – g )
⇒ CD/AB = BC/AE
hay CD/15 = 10/12 ⇔ CD = (10.15)/12 ⇒ CD = 18 ( cm )
Áp dụng định lý Py – ta – go vào tam giác vuông ABE có:
BE2 = AE2 + AB2 ⇒ BE2 = 102 + 152 ⇒ BE ≈ 18,0( cm )
Áp dụng định lý Py – ta – go vào tam giác vuông BCD có:
BD2 = CD2 + BC2 ⇒ BD2 = 182 + 122 = 468 ⇒ BD ≈ 21,6( cm )
Áp dụng định lý Py – ta – go vào tam giác vuông EBD có:
ED2 = BD2 + BE2 ⇒ ED2 = 325 + 468 = 793 ⇒ ED ≈ 28,2( cm )
c) Ta có:
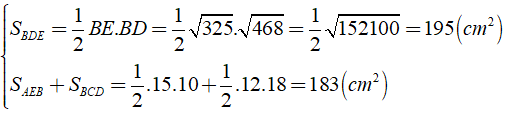
Vậy SBED > SAEB + SBCD
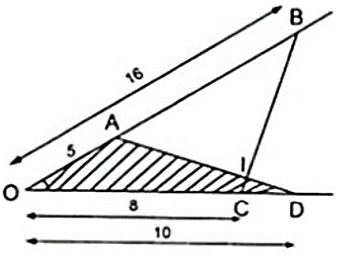
Bài 3: Trên một cạnh của một góc xOy ( Ox ≠ Oy ) đặt các đoạn thẳng OA = 5cm, OB = 16cm
Trên cạnh thứ hai của góc đó đặt các đoạn thẳng OC = 8cm, OD = 10cm.
a) Chứng minh Δ OCB ∼ Δ OAD
b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng Δ IAB và Δ ICD có các góc bằng nhau từng đôi một
Lời giải:
a) Xét Δ OCB và Δ OAD có
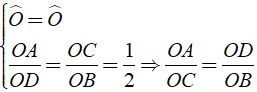
⇒ Δ OCB ∼ Δ OAD ( c – g – c )
b) Ta có: Δ OCB ∼ Δ OAD
⇒ ADOˆ = CBOˆ hay IDCˆ = IBAˆ
Mà CIDˆ = AIBˆ (vì đối đỉnh) ⇒ ICDˆ = IABˆ
Bài giảng: Bài 6: Trường hợp đồng dạng thứ hai – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Bài giảng: Bài 7: Trường hợp đồng dạng thứ ba – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

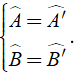

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn