Cách chia đơn thức cho đơn thức (cực hay, có lời giải)

Bài viết Cách chia đơn thức cho đơn thức với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách chia đơn thức cho đơn thức cực.

Cách chia đơn thức cho đơn thức (cực hay, có lời giải)

1. Định nghĩa:

Với A và B là hai đơn thức,B ≠ 0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B. Q

Trong đó:

      . A là đơn thức bị chia.

      . B là đơn thức chia.

      . Q là đơn thức thương (hay gọi là thương)

Kí hiệu: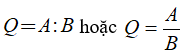

2. Quy tắc

Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với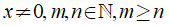
thì:

x^m : xⁿ = x^m-n       nếu m > n

x^m : xⁿ = 1       nếu m = n
Và (xⁿ)^m = x^n.m

Quy tắc:

Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:

      + Chia hệ số của đơn thức A cho hệ số của đơn thức B.

      + Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

      + Nhân các kết quả vừa tìm được với nhau.

Ví dụ 1. Tính (-4)¹³ : 4¹⁰

A. – 64
            B. 12
            C. -12
            D. 64

Lời giải

Ta có: (-4)¹³ : 4¹⁰ = (-4)¹³ : (-4)¹⁰ = (-4)³ = -64

( vì (-4)¹⁰ = (-1.4)¹⁰ = (-1)¹⁰.4¹⁰ = 1.4¹⁰ = 4¹⁰)

Chọn A.

Ví dụ 2. Tính 39x⁵ : 13x²

A.3x²
            B. – 3x³
            C. 3x³
            D. -3x²

Lời giải

39x⁵ : 13x² = (39 : 13).(x⁵ : x²) = 3x³

Chọn C.

Ví dụ 3. Tính 16x²y³ : (-4xy³)

A. – 4x.y
            B.4x²y
            C. – 4xy
            D. – 4x

Lời giải

16x²y³ : (-4xy³) = [16 : (-4)].(x² : x)(y³ : y³)

= -4x²-1.y³-3 = -4×1.y⁰ = -4x

Chọn D.

Ví dụ 4. Tính (2x²y²)³ : (2xy²)

A.4x⁵y⁴
            B. 2x²y
            C. 3x⁵y³
            D. 3x³y³

Lời giải

(2x²y²)³ : (2xy²) = 8x⁶y⁶ : 2xy²

= (8 : 2).(x⁶ : x).(y⁶ : y²) = 4x⁵y⁴

Chọn A.

Câu 1. Tính 6¹² : (-6)⁸

A. 6⁴
            B. – 6⁴
            C. 6²
            D. – 6²

Lời giải:

6¹² : (-6)⁸ = 6¹² : 6⁸ = 6^12-8 = 6⁴

(-6)⁸ = (-1.6⁸) = (-1)⁸.6⁸ = 1.6⁸ = 6⁸

Chọn A

Câu 2. Tính (-8x⁶) : 2x³

A. 4x²
            B. 4x³
            C. – 4x³
            D. -4x²

Lời giải:

(-8x⁶) : 2x³ = (-8:2).(x⁶ : x³)

= -4x⁶-3 = -4x³

Chọn C.

Câu 3. Tính (2x³y⁴)³ : (x²y)⁴

A. 6xy⁷
            B. 8xy⁷
            C. 6x³y
            D. 8xy⁸

Lời giải:

(2x³y⁴)³ : (x²y)⁴ = 8x⁹y¹² : x⁸y⁴ = 8xy⁸

Chọn D.

Câu 4. Tính 12x⁵y⁷ : (-2x²y³)²

A. -6xy
            B. 3xy
            C. – 3xy
            D. 6xy

Lời giải:

12x⁵y⁷ : (-2x²y³)² = 12x⁵y⁷ : 4x⁴y⁶ = 3xy

Chọn B.

Câu 5. Tính (-8x²y⁵):(2xy)

A. – 4xy²
            B. – 4xy⁵
            C. – 4xy⁴
            D. 4x²y⁵

Lời giải:

(-8x²y⁵):(2xy) = -4xy⁴

Chọn C.

Câu 6. Tính (-2x³y⁵)³ : (2x³y⁵)²

A. 2x²y⁴
            B. -2x³y⁵
            C. – 2x²y⁴
            D. – 2x³y⁵

Lời giải:

(-2x³y⁵)³ : (2²x³y⁵)2 = -8x⁹y¹⁵ : 4x⁶y¹⁰ = -2x³y⁵

Chọn D.

Câu 7. Tính (3x³y⁴)² : (-xy²)³

A. – 9x²y²
            B. – 9x³y²
            C. 9x²y³
            D. 3x²y³

Lời giải:

(3x³y⁴)² : (-xy²)³ = 9x⁶y⁸:(-x³y⁶) = -9x³y²

Chọn B.

Câu 8: Tính (-8x³y³):(-xy)³

A. 8
            B. 8xy
            C. 8x
            D. 8y

Lời giải:

(-8x³y³):(-xy)³ = (-8x³y³):(-x³y³) = 8

Chọn A.

Câu 9. Tính (-3x²y³)² : 3xy²

A. – xy

B. – x²y²

C. – 3xy

D. 3x³y⁴

Lời giải:

Ta có: (-3x²y³)² : 3xy² = 9x⁴y⁶ : 3xy² = 3x³y⁴

Chọn D.

Câu 10. Tính x⁴y⁷ : (-2x²y)²

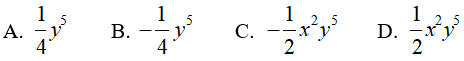
Lời giải:

Ta có: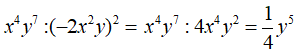

Chọn A .

   

Xem thêm các dạng bài tập Toán lớp 8 chọn lọc, có đáp án hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

---