Cách giải bài tập Công thức biến đổi tích thành tổng (cực hay, chi tiết) – Tổng hợp các dạng bài tập Toán 10 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 10.-Cách giải bài tập Công thức biến đổi tích thành tổng (cực hay, chi tiết)
Cách giải bài tập Công thức biến đổi tích thành tổng (cực hay, chi tiết)
Bài viết Cách giải bài tập Công thức biến đổi tích thành tổng với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách giải bài tập Công thức biến đổi tích thành tổng.
Cách giải bài tập Công thức biến đổi tích thành tổng (cực hay, chi tiết)
Để làm bài tập dạng này, ta phải nắm vững công thức biến đổi tích thành tổng và áp dụng để biến đổi.
Công thức biến đổi tích thành tổng:
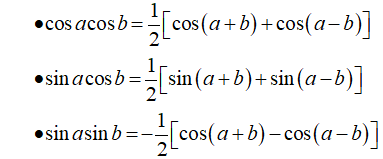
Ví dụ 1: Tính giá trị của biểu thức 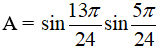
Hướng dẫn giải:
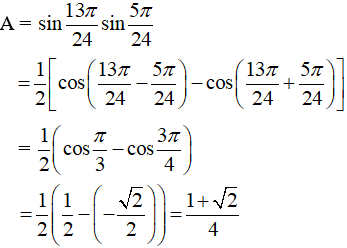
Ví dụ 2: Biến đổi thành tổng: A = 2 sinx.sin2x.sin3x
Hướng dẫn giải:
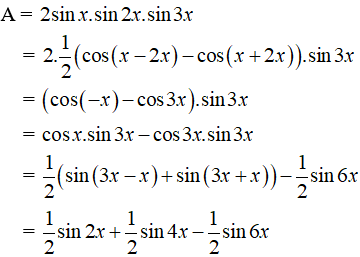
Ví dụ 3: Cho 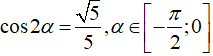 . Tính P = sinα.cos3α + cos2α
. Tính P = sinα.cos3α + cos2α
Hướng dẫn giải:
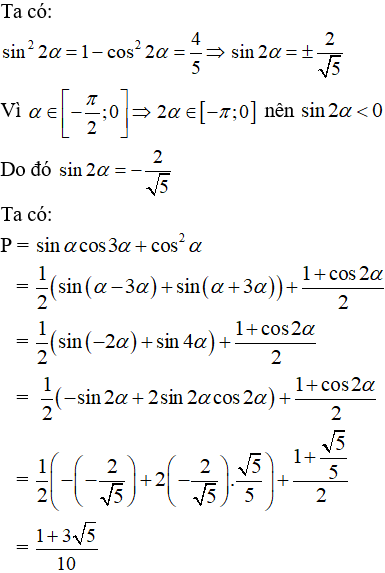
Ví dụ 4: Rút gọn biểu thức lượng giác sau:
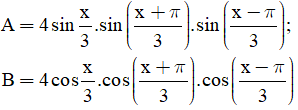
Hướng dẫn giải:
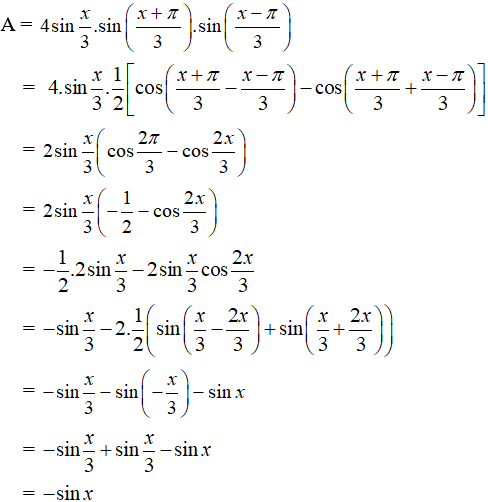
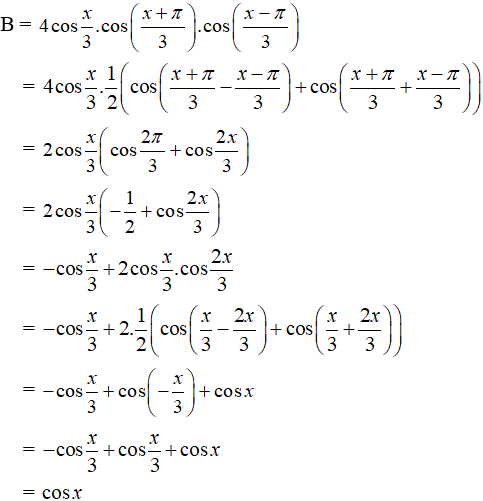
Ví dụ 5: Chọn đáp án đúng: Giá trị của biểu thức A = cos15o.cos45o.cos75o là:

Hướng dẫn giải:
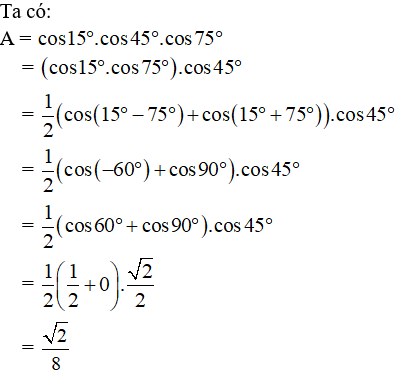
Đáp án C
Bài 1. Biến đổi tích thành tổng A = 2sin(x + y)cos(x – y).
Hướng dẫn giải:
A = 2sin(x + y)cos(x – y)
= sin2x + sin2y
Bài 2. Biến đổi tích thành tổng A = 2cos(x + y)cos(x – y).
Hướng dẫn giải:
A = 2cos(x + y)cos(x – y)
= cos2x + cos2y
Bài 3. Biến đổi tích thành tổng A = 4sin 3a. sin 2a. sin a.
Hướng dẫn giải:
A = 4sin 3a. sin 2a. sin a
= –2 sin 2a. (cos 4a – cos 2a)
= –2cos 4a. sin 2a + 2sin 2a. cos 2a
= –(sin 6a – sin 2a) + sin 4a
= –sin 6a + sin 4a + sin 2a.
Bài 4. Biến đổi tích thành tổng A = 2sin4a.sin2a + 2sin22a
Hướng dẫn giải:
A = 2sin4a.sin2a + 2sin22a
= -(cos6a – cos2a) + 1 – cos4a
= -cos6a – cos4a + cos2a + 1
Bài 5. Chứng minh đẳng thức sau
sina + sin2a + sin3a +…+sinna = sinna2.sin(n+1)a2sina2
Hướng dẫn giải:
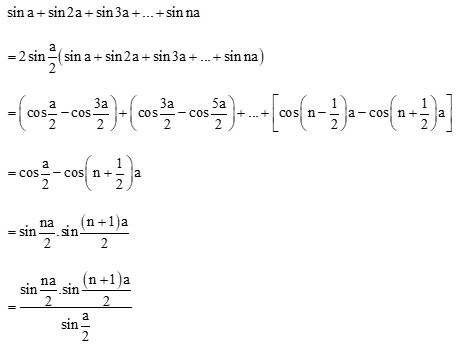
Bài 6. Tính sin5π24sinπ24.
Bài 7. Tính cos2xsin5xcos 3x
Bài 8. Tính sin40ocos10ocos8o.
Bài 9. Biến đổi tích thành tổng 4cos(a – b)cos(b – c)cos(c – a).
Bài 10. Tính cosπ15cos2π15cos3π15…cos7π15.
Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:
Lời giải bài tập lớp 10 sách mới:

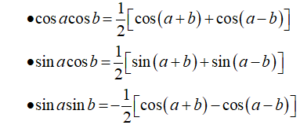
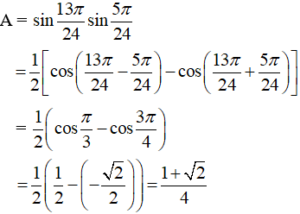

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn