Cách giải bất phương trình (hay, chi tiết) – Chuyên đề Toán 8 tổng hợp phương pháp giải các dạng bài tập Toán 8 hay, chi tiết giúp bạn học tốt Toán lớp 8.-Cách giải bất phương trình (hay, chi tiết)
Cách giải bất phương trình (hay, chi tiết)
Với Cách giải bất phương trình hay, chi tiết môn Toán lớp 8 phần Đại số sẽ giúp học sinh ôn tập, củng cố kiến thức từ đó biết cách làm các dạng bài tập Toán lớp 8 Chương 4: Bất phương trình bậc nhất một ẩn để đạt điểm cao trong các bài thi môn Toán 8.
Cách giải bất phương trình (hay, chi tiết)
Dạng bài: Giải bất phương trình
A. Phương pháp giải
Sử dụng các hằng đẳng thức, các quy tắc chuyển vế hoặc nhân (chia) với một số khác 0 để giải các bất phương trình đã cho.
*Giải bất phương trình bậc nhất một ẩn
Bước 1: Áp dụng quy tắc (quy tắc chuyển vế hoặc quy tắc nhân với một số) để đưa bất phương trình về dạng 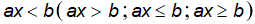 .
.
Bước 2: Kết luận nghiệm của bất phương trình.
B. Ví dụ minh họa
Câu 1: Giải các bất phương trình (theo quy tắc chuyển vế)
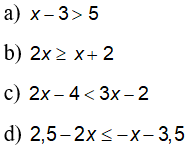
Lời giải:
a) Ta có: 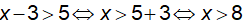
Vậy tập nghiệm của bất phương trình là
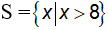
b) Ta có: 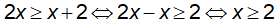
Vậy tập nghiệm của bất phương trình là
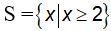
c) Ta có: 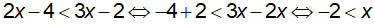
Vậy tập nghiệm của bất phương trình là
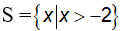
d) Ta có: 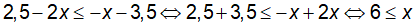
Vậy tập nghiệm của bất phương trình là
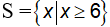
Câu 2: Giải các bất phương trình sau
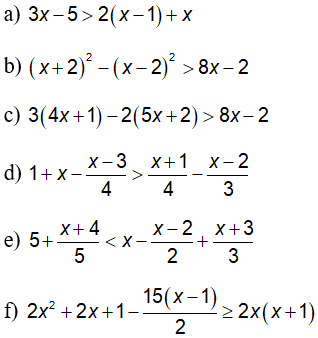
Lời giải:
a) Ta có:
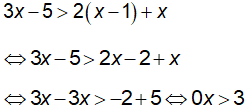
Vậy bất phương trình vô nghiệm.
b) Ta có:
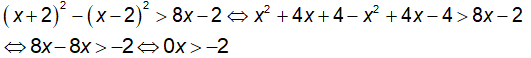
Vậy bất phương trình có vô số nghiệm.
c) Ta có:
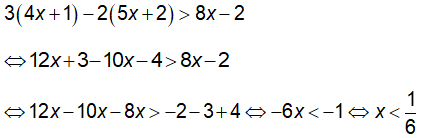
Vậy tập nghiệm của bất phương trình là
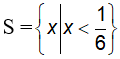
d) Ta có:
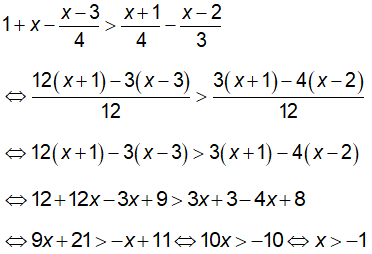
Vậy tập nghiệm của bất phương trình là
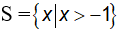
e) Ta có:
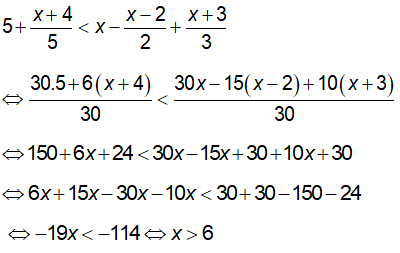
Vậy tập nghiệm của bất phương trình là
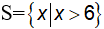
f) Ta có:
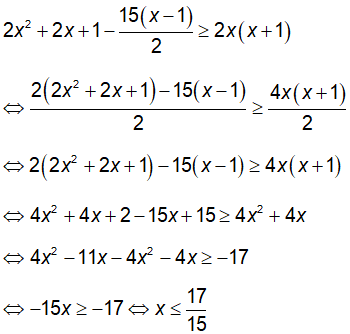
Vậy tập nghiệm của bất phương trình là
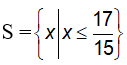
Câu 3: Giải các bất phương trình sau và biểu diễn tập nghiệm của mỗi bất phương trình trên một trục số
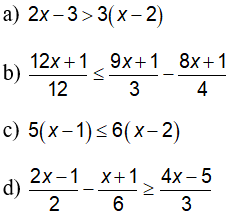
Giải
a) Ta có
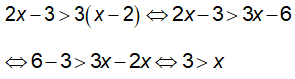
Vậy tập nghiệm của bất phương trình là
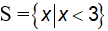
+) Biểu diễn trục số

b) Ta có
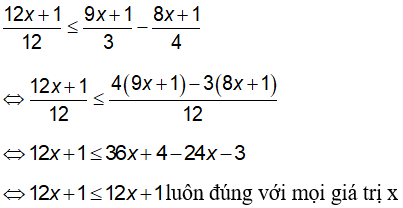
Vậy tập nghiệm của bất phương trình là 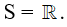
+) Biểu diễn trên trục số:
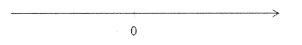
c) Ta có:
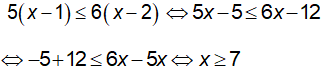
Vậy tập nghiệm của bất phương trình là
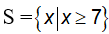
+) Biểu diễn trên trục số:
d) Ta có:
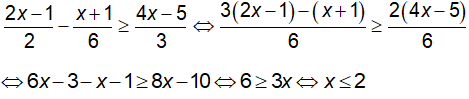
Vậy tập nghiệm của bất phương trình là
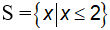
+) Biểu diễn trên trục số:

C. Bài tập tự luyện
Câu 1: Giải các bất phương trình sau:
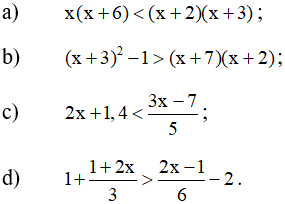
Câu 2: Với giá trị nào của x thì:
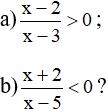
Câu 3: Giải bất phương trình:
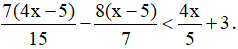
Câu 4: Khi giải các bất phương trình 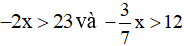 , một học sinh thực hiện như sau:
, một học sinh thực hiện như sau:
a) Ta có:
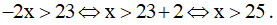
Vậy nghiệm là x>25.
b) Ta có:
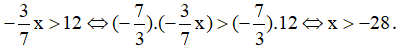
Vậy nghiệm là x>-28.
Em có đồng ý với học sinh đó hay không? Nếu không thì giải thích?
Câu 5: Giải các bất phương trình:
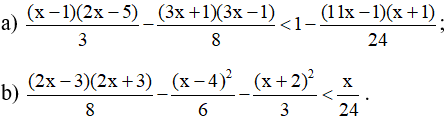
Câu 6: Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
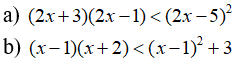
Câu 7: Giải các bất phương trình sau: (Biến đổi đặc biệt)
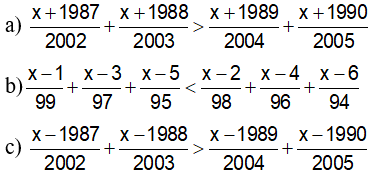
D. Bài tập bổ sung
Bài 1. Giải các bất phương trình sau:
a) x-26+x-35<x-44+x-17
b) x+27+x+45<x+63+x+18
Bài 2. Giải các bất phương trình sau:
a) 1-2×4-2<1-5×8
b) 35-x>3-5×2+3x
Bài 3. Giải các bất phương trình sau:
a) x-412-x≤-3(x+3)4-x-56
b) 3 + 5x ³ (4 + 2x) – (5 + 6x).
Bài 4. Giải các bất phương trình sau:
a) (x + 5)(x – 1) ≤ 2x(x – 1).
b) 3(x – 1)(2x – 1) ≥ 5(x + 8)(x – 1).
Bài 5. Giải các bất phương trình sau:
a) 8x + 4 < 5(2x + 5).
b) 3x + 8 < 5(x + 2) – 2.
Xem thêm các dạng bài tập Toán lớp 8 chọn lọc hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

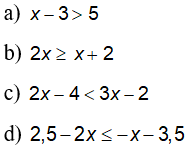

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn