Cách giải hệ phương trình bằng phương pháp cộng đại số lớp 9 (cực hay) – Tổng hợp các dạng bài tập Toán 9 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 9.-Cách giải hệ phương trình bằng phương pháp cộng đại số lớp 9 (cực hay)
Cách giải hệ phương trình bằng phương pháp cộng đại số lớp 9 (cực hay)
Bài viết Cách giải hệ phương trình bằng phương pháp cộng đại số lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải hệ phương trình bằng phương pháp cộng đại số lớp 9 (cực hay)
Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp(nếu cần) sao cho các hệ số của một ẩn nào đó(ẩn x hay y) trong hai phương trình của hệ bằng nhau hoặc đối nhau.
Bước 2: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới
Bước 3: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)
Bước 4: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Bước 5: Kết luận
Ví dụ 1: Giải hệ phương trình sau: 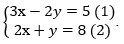
Hướng dẫn:
Nhân hai vế của pt (2) với 2 ta được:
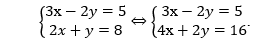
Cộng các vế tương ứng của hai phương trình ta có: 7x = 21 ⇔ x = 3.
Thay vào phương trình (2) ta được: 6 + y = 8 ⇔ y = 2
Vậy nghiệm của hệ phương trình là (x;y) = (3;2).
Ví dụ 2: Giải hệ phương trình sau: 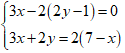
Hướng dẫn:
Ta có:
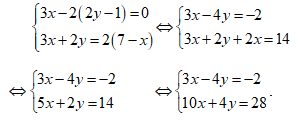
Cộng các vế tương ứng của hai phương trình ta có: 13x = 26 ⇔ x = 2.
Thay x = 2 vào phương trình thứ hai: 5.2 + 2y = 14 ⇔ y = 2.
Vậy nghiệm của hệ phương trình là (x;y) = (2;2).
Ví dụ 3: Giải hệ phương trình: 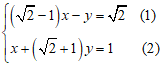
Hướng dẫn:
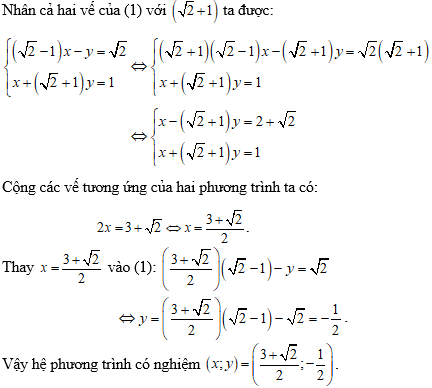
Câu 1: Hệ phương trình: 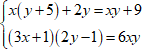 có nghiệm (x;y) = ?
có nghiệm (x;y) = ?
A. (x;y) = (2;1)
B. (x;y) = (1;2)
C. (x;y) = (2;–1)
D. (x;y) = (1;1)
Lời giải:
Ta có:
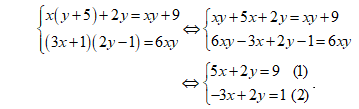
Trừ các vế tương ứng của hai phương trình ta có: 8x = 8 ⇔ x = 1.
Thay x = 1 vào phương trình thứ nhất: 5.1 + 2y = 9 ⇔ y = 2..
Vậy hệ phương trình có nghiệm là (x;y) = (1;2).
Chọn đáp án B.
Câu 2: Hệ phương trình sau: 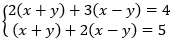 . Tổng x + y = ?
. Tổng x + y = ?
A. 4
B. 5
C. – 6
D. – 7
Lời giải:
Ta có:
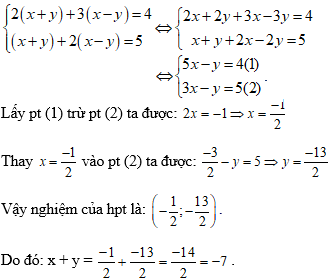
Chọn đáp án D.
Câu 3: Giải hệ phương trình sau: 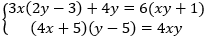 . So sánh xy với 0.
. So sánh xy với 0.
A. xy > 0
B. xy = 0
C. xy < 0
Lời giải:
Ta có:
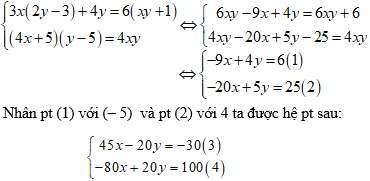
Cộng các vế tương ứng của pt (3) và pt (4) ta được: -35x = 70 ⇒ x = -2
Thế x = -2 vào pt (1) ta được: 18 + 4y = 6 ⇒ y = -3
Vậy nghiệm của hệ phương trình là: (-2;-3).
Do đó: xy = (–2).(–3) = 6 > 0.
Chọn đáp án A.
Câu 4: Cho hệ phương trình: 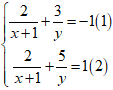 . Bạn An giải như sau thiếu bước nào?
. Bạn An giải như sau thiếu bước nào?

A. Bạn An chưa đặt điều kiện xác định của hệ.
B. Bạn An giải đủ các bước.
C. Bạn An chưa kết luận nghiệm.
Lời giải:
Chọn đáp án A.
Bạn Ạn chưa tìm ĐKXĐ của hệ vì hệ phương trình có chứa phân thức.
ĐKXĐ: x + 1 ≠ 0 và y ≠ 0 hay x ≠ -1 và y ≠ 0.
Câu 5: Cho hệ phương trình sau: 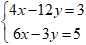 Không giải hãy dự đoán hệ có bao nhiêu nghiệm?
Không giải hãy dự đoán hệ có bao nhiêu nghiệm?
A. Có vô số nghiệm
B. có nghiệm duy nhất
C. Không có nghiệm
D. Có hai nghiệm.
Lời giải:
Chọn đáp án B. Vì 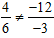 . suy ra hệ phương trình có nghiệm duy nhất.
. suy ra hệ phương trình có nghiệm duy nhất.
Câu 6: Cho hệ phương trình sau: 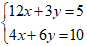 . Khẳng định nào sau đây là dúng?
. Khẳng định nào sau đây là dúng?
A. x > y
B. x = y
C. x < y
D. x + y = 0
Lời giải:
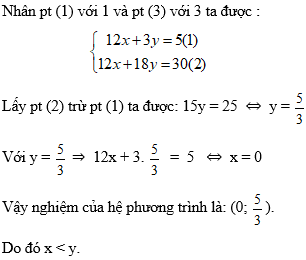
Chọn đáp án C.
Câu 7: Cho hệ phương trình sau: 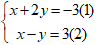 . kết quả của x + y – 1 = ?
. kết quả của x + y – 1 = ?
A. 1
B. – 1
C. 2
D. – 2
Lời giải:
Lấy pt (1) trừ pt (2) ta được: 3y = – 6 ⇔ y = – 2.
Thay y = – 2 vào pt (2) ta được: x – (– 2) = 3 ⇒ x + 2 = 3 ⇒ x = 3 – 2 = 1
Vậy nghiệm của hệ phương trình là:(1; – 2).
Do đó: x + y – 1 = 1 – 2 – 1 = – 2.
Chọn đáp án D.
Câu 8: Cho hệ phương trình sau: 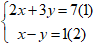 . Khẳng định nào sau đây là dúng?
. Khẳng định nào sau đây là dúng?
A. x + y < 0
B. x + y > 3
C. x + y > 0
D. x < y
Lời giải:
Nhân pt (1) với 1 và pt (2) với 3 ta được: 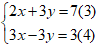
Lấy pt (3) cộng pt (4) ta được: 5x = 10 ⇔ x = 2.
Với x = 2 ⇒ 2 – y = 1 ⇔ y = 1.
Vậy nghiệm của hệ phương trình là: (2;1)
Do đó: x + y = 2 + 1 = 3 > 0.
Chọn đáp án C.
Câu 9: Nghiệm (x;y) = (5; –2) là nghiệm của hệ phương trình nào sau đây.

Lời giải:
Chọn đáp án B.
Vì thay nghiệm (x;y) = (5; –2) vào hệ phương trình. (B) thỏa mãn.
Ta có:
VT = 3x + 2y = 3.5 + 2. (– 2) = 11 = VP.
VT = x + 2y = 5 + 2.(–2) = 1 = VP.
Vậy (5; –2) là nghiệm của hệ phương trình B.
Câu 10: Cho hệ phương trình sau: 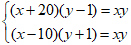 . Kết quả của (x – y + 1) : 2 = ?
. Kết quả của (x – y + 1) : 2 = ?
A. 10
B. – 15
C. 17
D. 19
Lời giải:
Ta có:
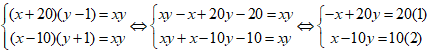
Lấy pt (1) cộng pt (2) ta được: 10y = 30 ⇔ y = 3
Với y = 3 ⇒ x = 10 + 10.3 = 40
Vậy nghiệm của hệ phương trình là: (40;3)
Do đó: (x – y + 1) : 2 = (40 – 3 + 1) : 2 = 19.
Chọn đáp án D.
Bài 1. Cho hệ phương trình: x+3-2y+1=22x+3+y+1=4.
a) Điều kiện xác định của phương trình;
b) Tìm nghiệm của hệ phương trình.
Bài 2. Cho hệ phương trình: 2(x2-2x)+y+1=03(x2-2x)-2y+1=-7. Hãy so sánh xy với 0?
Bài 3. Cho hệ phương trình: 7x-7-5y+6=535x-7+3y+6=216.
a) Giải hệ phương trình;
b) Hãy tính 7(x – y2).
Bài 4. Giải hệ phương trình sau: x+by=-2bx-ay=-3. Xác định hệ số a và b, biết rằng hệ phương trình:
a) Có nghiệm là (1; – 2);
b) Có nghiệm là (2-1;2).
Bài 5. Cho hệ phương trình sau: 2x+13-y+14=4x-2y+252x-34-y-43=-2x+2y-2(1). Hãy tìm các giá trị của m để nghiệm của hệ phương trình (1) cũng là nghiệm của phương trình:
6mx – 5y = 2m – 4.
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án chi tiết hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn