Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm lớp 9 (cực hay, có đáp án) – Chuyên đề Toán 9 tổng hợp phương pháp giải các dạng bài tập Toán 9 hay, chi tiết giúp bạn học tốt Toán 9.-Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm lớp 9 (cực hay, có đáp án)
Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm lớp 9 (cực hay, có đáp án)
Bài viết Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm.
Cách làm bài toán parabol cắt đường thẳng thỏa mãn điều kiện về tọa độ giao điểm lớp 9 (cực hay, có đáp án)
Cho parabol (P): y = ax2 (a ≠ 0) và đường thẳng y = mx + n.
Bước 1: Viết phương trình hoành độ giao điểm của parabol và đường thẳng.
ax2 = mx + n ⇔ ax2 – mx – n = 0 (*)
Bước 2: Xét điều kiện để parabol có điểm chung với đường thẳng:
– TH1: Parabol tiếp xúc với đường thẳng (có 1 điểm chung) ⇒ phương trình hoành độ giao điểm có nghiệm kép (Δ = 0 hoặc Δ’ = 0).
– TH2: Parabol cắt đường thẳng tại hai điểm phân biệt (có 2 điểm chung phân biệt) ⇒ phương trình hoành độ giao điểm có hai nghiệm phân biệt (Δ > 0 hoặc Δ’ > 0).
Bước 3: Xét điều kiện về tọa độ giao điểm:
+) Đường thẳng (d) cắt parabol (P) tại hai điểm có tung độ dương ⇒ a > 0.
+) Đường thẳng (d) cắt parabol (P) tại hai điểm có tung độ âm ⇒ a < 0.
+) Đường thẳng (d) cắt parabol (P) tại hai điểm có hoành độ cùng dấu ⇔ phương trình hoành độ giao điểm có hai nghiệm cùng dấu 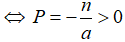 hay a.n < 0.
hay a.n < 0.
+) Đường thẳng (d) cắt parabol (P) tại hai điểm có hoành độ dương ⇔ phương trình hoành độ giao điểm có hai nghiệm dương 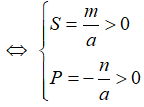
+) Đường thẳng (d) cắt parabol (P) tại hai điểm có hoành độ âm ⇔ phương trình hoành độ giao điểm có hai nghiệm âm 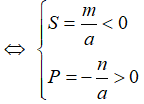
+) Đường thẳng (d) cắt (P) tại hai điểm có hoành độ trái dấu ⇔ phương trình hoành độ giao điểm có hai nghiệm trái dấu 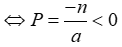 hay a.n > 0.
hay a.n > 0.
+) Đường thẳng (d) cắt (P) tại hai điểm có tọa độ thỏa mãn biểu thức cho trước: Sử dụng hệ thức Vi-ét, kết hợp biến đổi biểu thức.
Bước 4: Kết luận.
Ví dụ 1: Đường thẳng nào sau đây cắt đồ thị hàm số 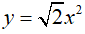 tại hai điểm phân biệt có hoành độ dương?
tại hai điểm phân biệt có hoành độ dương?

Lời giải
Chọn B
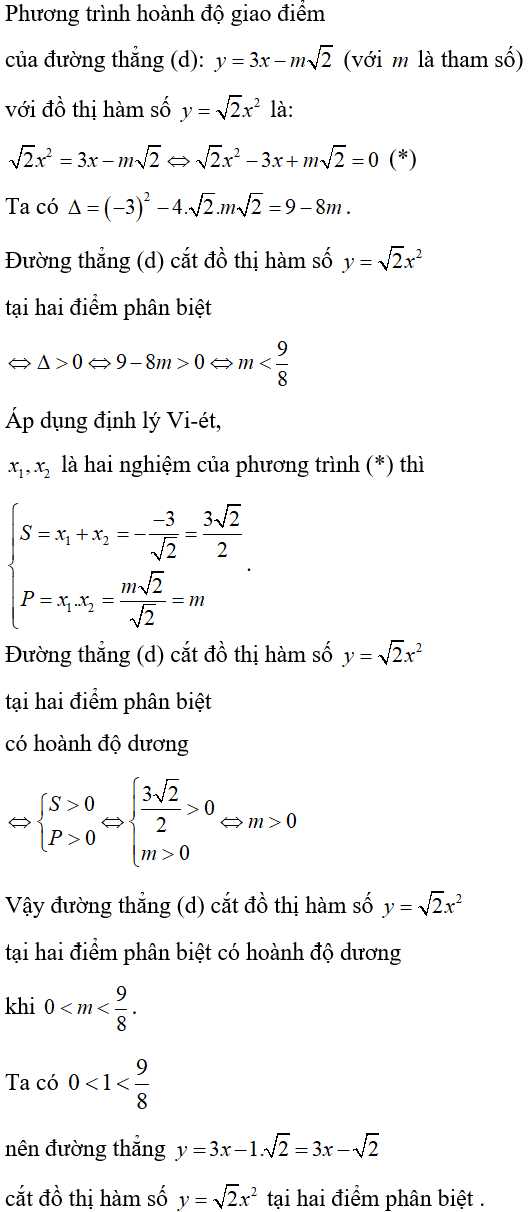
Ví dụ 2: Cho parabol (P): y = x2 và đường thẳng (d): y = x + m (với m là tham số). Giá trị của để (d) cắt (P) tại hai điểm phân biệt có hoành độ trái dấu là:

Lời giải
Chọn D

Ví dụ 3: Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 3 (với m là tham số, m ≠ 0). Giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ là các số nguyên.

Lời giải
Chọn B

Bài 1: Cho parabol (P): y = x2 và đường thẳng (d): y = (1 – 3m)x – m2 (với m là tham số). Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ đều là các số âm.

Lời giải:
Đáp án A

Bài 2: Tìm m ∈ Z để parabol (P): y = x2 cắt đường thẳng (d): y = (m – 1)x + m + 2 (với m là tham số) tại hai điểm phân biệt có hoành độ dương.

Lời giải:
Đáp án D

Bài 3: Có bao nhiêu giá trị của tham số m để đường thẳng (d): y = 2mx + 4 (m là tham số) và parabol (P): y = x2 cắt nhau tại hai điểm phân biệt có hoành độ thỏa mãn (x1 + x2)2 = mx1.x2?

Lời giải:
Đáp án B
Bài 4: Số giá trị nguyên của m để đường thẳng (d): y = mx + m + 1 và parabol (P): y = x2 cắt nhau tại hai điểm phân biệt có tọa độ (x1; y1) và (x2; y2) thỏa mãn y1 + y2 < 5 là:

Lời giải:
Đáp án A

Bài 5: Tìm giá trị của tham số m để đường thẳng (d): y = -x + 2m và parabol (P): 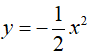 cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn 3x1 + 5x2 = 5.
cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn 3x1 + 5x2 = 5.

Lời giải:
Đáp án A
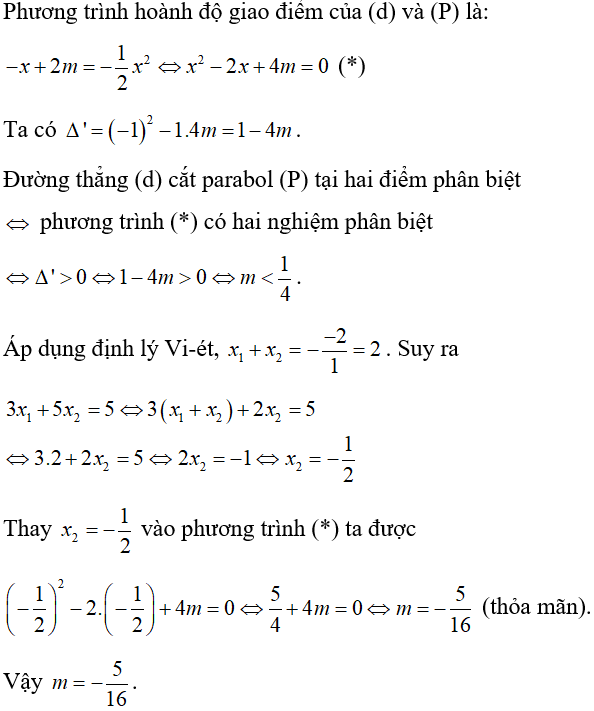
Bài 6: Đường thẳng (d): y = 2x + 5 cắt parabol (P): y = ax2 (x ≠ 0) tại điểm có tung độ bằng 3. Giá trị của a và tọa độ hai giao điểm là:

Lời giải:
Đáp án A
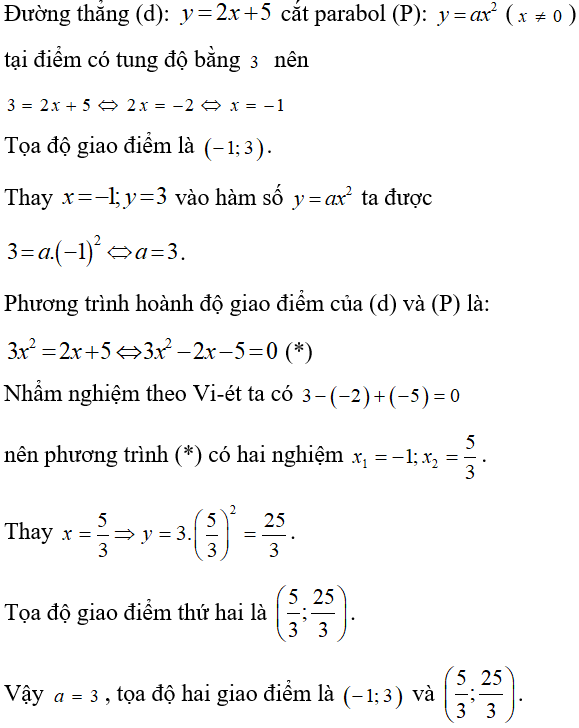
Bài 7: Số các giá trị nguyên của tham số m để đường thẳng (d): y = 6x – m cắt parabol (P): y = x2 tại hai điểm phân biệt có hoành độ x1, x2 sao cho x1x2 ≥ -2.

Lời giải:
Đáp án C

Bài 8: Cặp đường thẳng và parabol nào sau đây cắt nhau tại hai điểm có hoành độ cùng dấu?
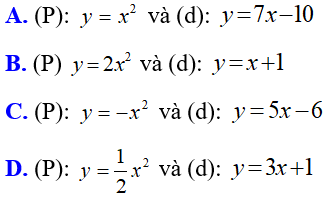
Lời giải:
Đáp án A

Bài 9: Tìm m để đồ thị hàm số y = mx2 (m ≠ 0) và đường thẳng y = 2(m – 1)x – m cắt nhau tại hai điểm có hoành độ x1, x2 thỏa mãn 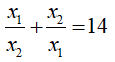

Lời giải:
Đáp án A
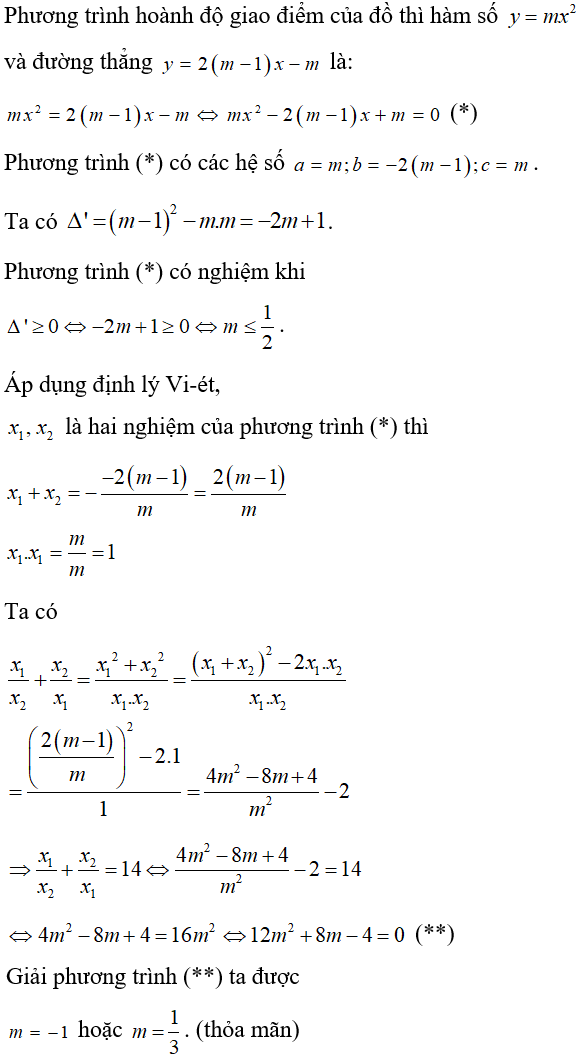
Bài 10: Cho parabol (P): y = x2 và đường thẳng (d): y = (2m + 1)x + 3 (m là tham số). Tìm m để (P) cắt (d) tại hai điểm có hoành độ x1, x2 sao cho |x1| – |x2| = 5 và x1 < x2

Lời giải:
Đáp án B
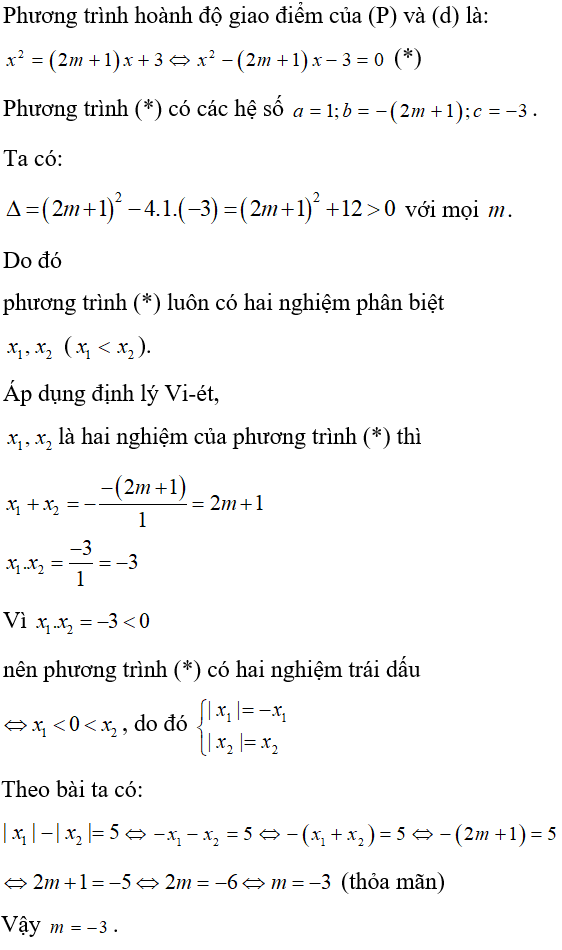
Bài 1. Cho parabol (P): y=12×2 và (d): y=12x+n. Tìm các giá trị của n để:
a) (P) tiếp xúc với (d);
b) (P) và (d) cắt nhau tại hai điểm phân biệt;
c) (P) và (d) cắt nhau tại hai điểm nằm ở hai phía trục tung.
Bài 2. Cho parabol (P): y = – x2 và đường thẳng đi qua điểm M( 0; – 1) có hệ số góc là k.
a) Viết phương trình đường thẳng d. Chứng minh rằng với mọi giá trị của k thì (d) luôn cắt (P) tại hai điểm phân biệt A và B;
b) Gọi hoành độ của A, B là x1, x2. Chứng minh: x1-x2≥2;
c) Chứng minh tam giác AOB vuông.
Bài 3. Cho parabol (P) có đồ thị đi qua gốc tọa độ và đi qua điểm A(1;-14). Với giá trị nào của m thì đường thằng d: cắt (P) tại hai điểm có hành độ x1, x2 sao cho 3x1 + 5x2 = 5.
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = mx – m + 1. Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt A và B hoành độ x1, x2 có thỏa mãn:
a) x1+x2=4 b) x1 = 9x2
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = 2mx – 2m + 3.
a) Tìm tọa độ các điểm thuộc điểm (P) biết tung độ của chúng bằng 2;
b) Chứng minh rằng với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt;
c) Gọi y1, y2 là tung độ các giao điểm của (d) và (P). Tìm giá trị của M để y1 + y2 < 9.
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

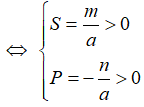
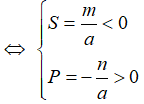

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn