Cách nhận dạng đồ thị hàm số bậc 3 (cực hay) – Tổng hợp các dạng bài tập Toán 12 với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 12.-Cách nhận dạng đồ thị hàm số bậc 3 (cực hay)
Cách nhận dạng đồ thị hàm số bậc 3 (cực hay)
Bài viết Cách nhận dạng đồ thị hàm số bậc 3 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách nhận dạng đồ thị hàm số bậc 3.
Cách nhận dạng đồ thị hàm số bậc 3 (cực hay)
Bài giảng: Cách nhận dạng đồ thị hàm số – Cô Nguyễn Phương Anh (Giáo viên Meraki Center)
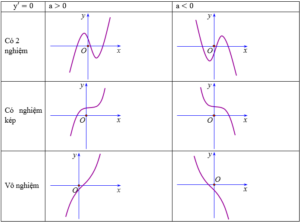
Các dạng đồ thị của hàm số bậc 3 y = ax3 + bx2 + cx + d (a ≠ 0)
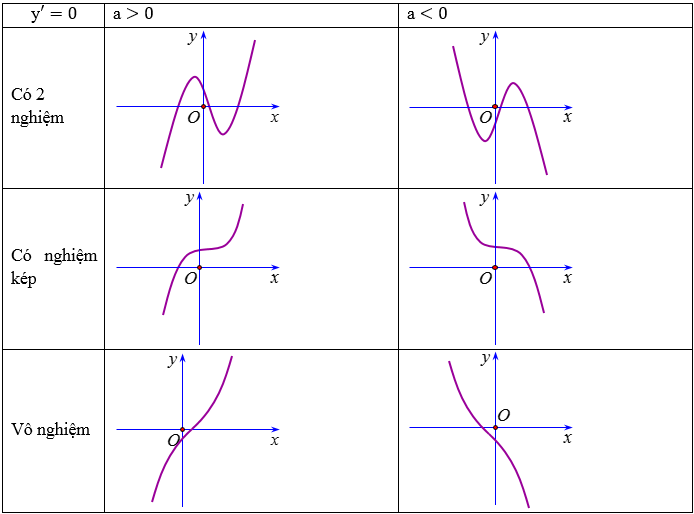
Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0
Đồ thị hàm số bậc ba luôn nhận điểm uốn làm tâm đối xứng
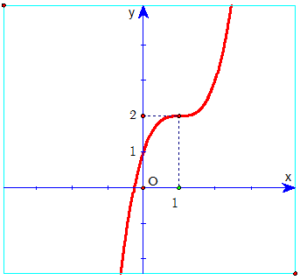
Ví dụ 1: Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
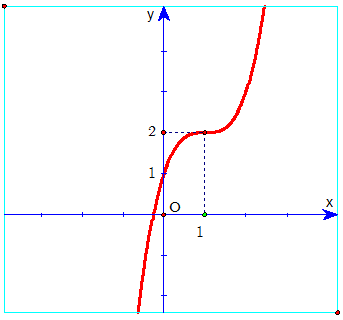
A. y = x3 – 3x + 1.
B. y = -x3 + 3x2 + 1.
C. y = x3 – 3x2 + 3x + 1.
D. y = -x3 – 3x2 – 1.
Hướng dẫn
Nhìn dạng đồ thị thấy a > 0 , suy ra loại B, D.
Mặt khác hàm số không có cực trị nên loại A.
Chọn C.
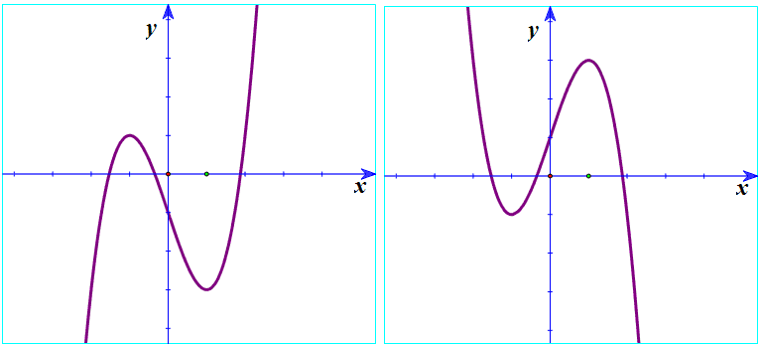
Ví dụ 2: Cho hàm số bậc 3 có dạng: y = f(x) = ax3 + bx2 + cx + d.
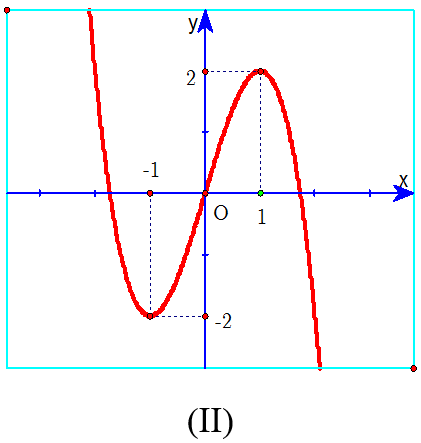
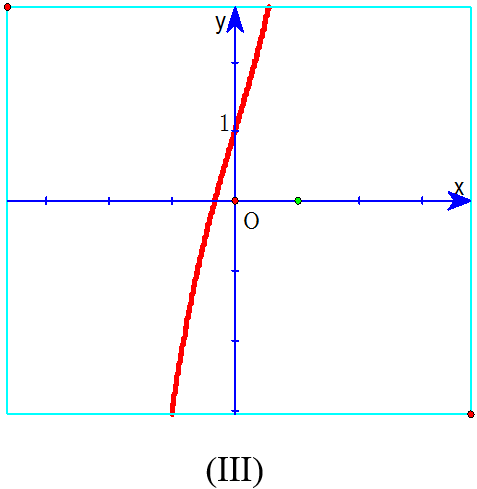
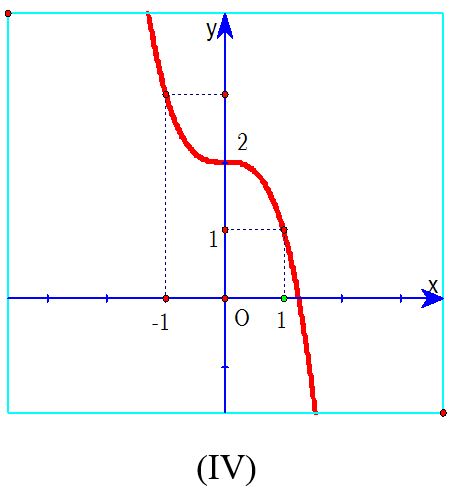
Hãy chọn đáp án đúng?
A. Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có nghiệm kép.
B. Đồ thị (II) xảy ra khi a ≠ 0 và f'(x) = 0 có hai nghiệm phân biệt.
C. Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.
D. Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm.
Hướng dẫn
Hàm số của đồ thị (II) có a < 0 nên điều kiện a ≠ 0 chưa đảm bảo. Do đó loại phương án B.
Hàm số của đồ thị (I) có a > 0 nên loại luôn phương án C.
Hàm số của đồ thị (IV) có a < 0 nên loại luôn phương án A.
Chọn D.
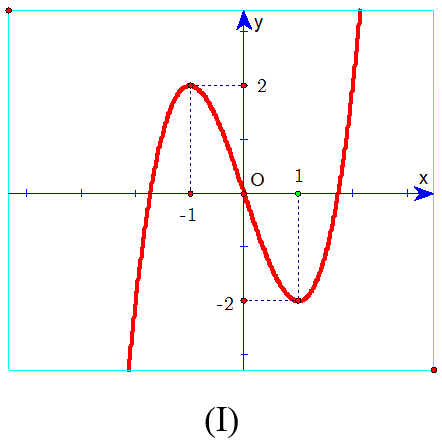
Ví dụ 3: Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên.
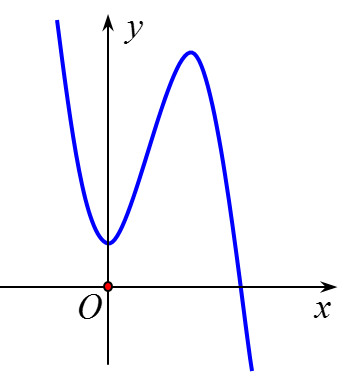
Mệnh đề nào dưới đây đúng?
A. a < 0,b > 0,c > 0,d > 0.
B. a < 0,b < 0,c = 0,d > 0.
C. a > 0,b < 0,c > 0,d > 0.
D. a < 0,b > 0,c = 0,d > 0.
Hướng dẫn
Từ hình dáng đồ thị ta suy ra hệ số a < 0,d > 0 loại đáp án C.
Ta có: y’ = 3ax2 + 2bx + c
Vì hàm số đạt cực tiểu tại điểm x = 0 nên y'(0) = 0 ⇒ c = 0 loại đáp án A.
Khi đó: y’ = 0 ⇔ 3ax2 + 2bx = 0 ⇔ x = 0 hoặc x = -2b/3a
Do hoành độ điểm cực đại dương nên -2b/3a > 0, mà a < 0 ⇒ b > 0.
Chọn D.
Trong các câu hỏi dưới đây, hãy tìm hàm số có đồ thị tương ứng với đồ thị trong hình vẽ:
Bài 1:
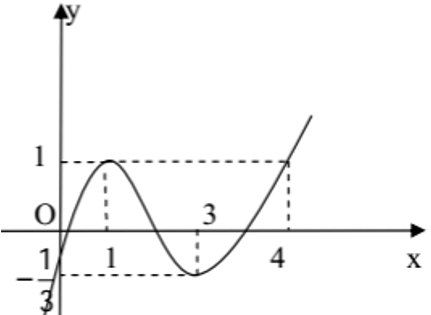
A. y = -(1/3)x3 + 2x2 – 3x – 1/3
B. y = 1/3 x3 -3x2 + 4x – 1/3
C. y = x3 -6x2 + 9x – 1
D. y = 1/3x3 – 2x2 + 3x – 1/3
Lời giải:
Đáp án : D
Bài 2:
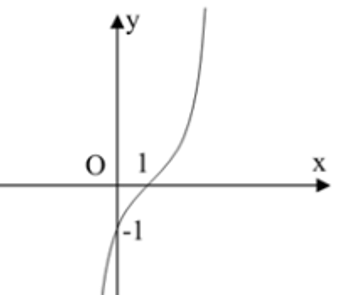
A. y = x3 – 3x2 + 3x + 1
B. y = x3 – 3x2 – 3x – 1
C. y = x3 – 3x2 + 3x – 1
D. y = -x3 + 3x2 – 3x – 1
Lời giải:
Đáp án : C
Bài 3:
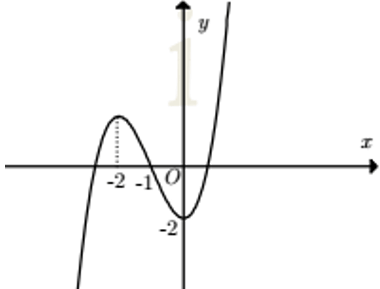
A. y = x3 + 3x2 – 2
B. y = x3 – 3x2 – 2
C. y = -x3 – 3x2 – 2
D. y = -x3 + 3x2 – 2
Lời giải:
Đáp án : A
Bài 4:
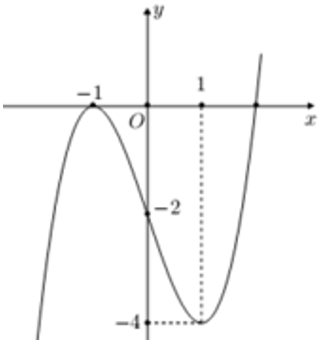
A. y = x3 – 2
B. y = x3 – 3x- 2
C. y = -x3 + 3x- 2
D. y = -x3 – 3x
Lời giải:
Đáp án : B
Bài 5:
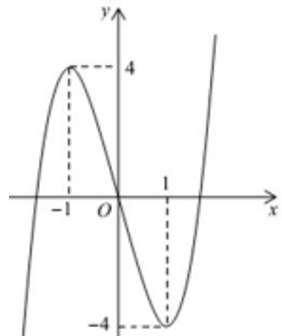
A. y = -x3 + 3x
B. y = x3 – 3x
C. y = 2x3 – 6x
D. y=-2x3 + 6x
Lời giải:
Đáp án : C
Bài 6:
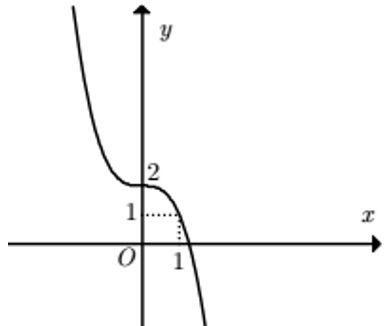
A. y = -x3 + 2
B. y = -x3 + 3x + 2
C. y = -x3 – x + 2
D. y = -x3 + 1
Lời giải:
Đáp án : A
Bài 7:
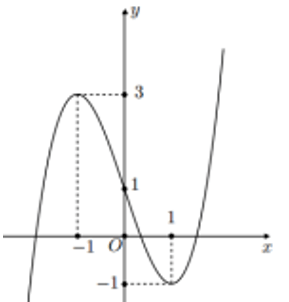
A. y = -x3 + 3x + 1
B. y = x3 – 3x + 1
C. y = -x3 + 3x + 2
D. y = x3 + 3x + 1
Lời giải:
Đáp án : B
Bài 8:
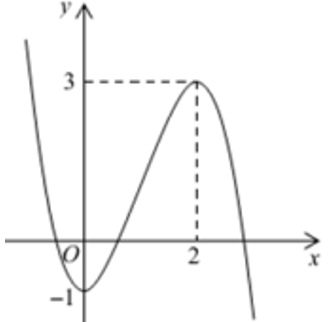
A. y = x3 – 3x2 – 1
B. y = -x3 + 3x2 – 1
C. y = -x3 + 6x2 – 1
D. y = -x3 + 3x2 – 4
Lời giải:
Đáp án : B
Bài 9:
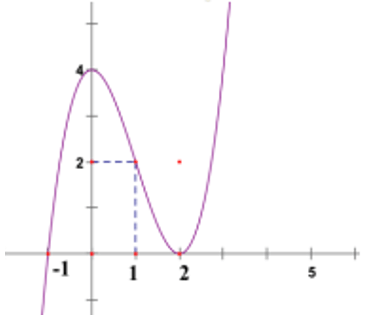
A. y = -x3 – 3x2 + 2
B. y = -x3 + 3x2 + 4
C. y = x3 – 3x2 + 2
D. y = x3 – 3x2 + 4
Lời giải:
Đáp án : D
Bài 10:
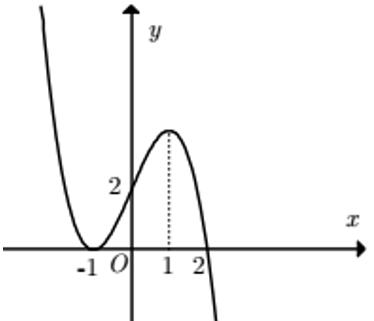
A. y = (x + 1)2(2 – x)
B. y = (x + 1)2(1 + x)
C. y = (x + 1)2(2 + x)
D. y = (x + 1)2(1 – x)
Lời giải:
Đáp án : A
Bài 11:
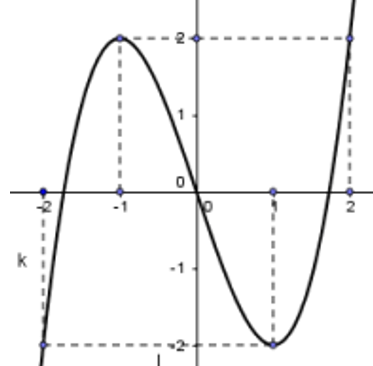
A. y = -x3
B. y = x3 – 3x
C. y = x4 – 4x2
D. y = x3 – 3x2
Lời giải:
Đáp án : B
Bài 12:
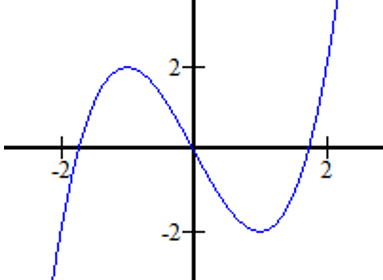
A. y = x3 – 3x
B. y = x3 – 3x2 + 3x – 1
C. y = -x3 + 3x
D. y = x3 + 3x
Lời giải:
Đáp án : A
Bài 13:
A. y = x3 – 3x+ 1
B. y = -x3 + 3x- 1
C. y = 2x3 – 6x+ 1
D. y = 2x3 – 3x2 + 1
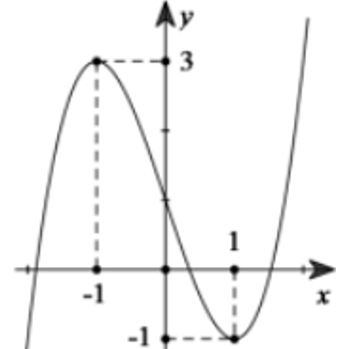
Lời giải:
Đáp án : A
Bài 14:
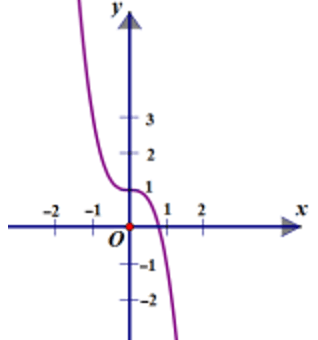
A. y = -x3 + 3x + 1
B. y = -2x3 + 1
C. y = -1/3 x3 + 2x + 1
D. y = 2x3 + 1
Lời giải:
Đáp án : B
Bài 15: Cho hàm số y = x3 + ax + b có đồ thị như hình bên. Chọn khẳng định đúng:
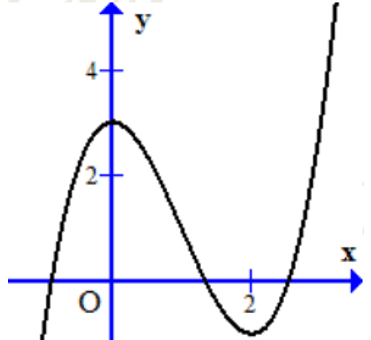
A. a < 0,b < 0
B. a > 0,b < 0
C. a > 0,b > 0
D. a < 0,b > 0
Lời giải:
Đáp án : D
Bài 16: Cho hàm số y = 1/3x3 + bx2 + cx + d có đồ thị như hình bên. Chọn khẳng định đúng:
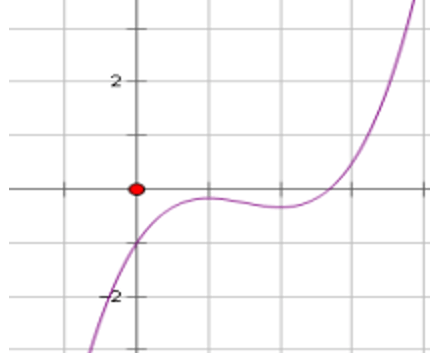
A. b < 0,c > 0,d > 0
B. b < 0,c > 0,d < 0
C. b > 0,c > 0,d < 0
D. b < 0,c < 0,d < 0
Lời giải:
Đáp án : B
Bài 17: Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình bên. Chọn khẳng định đúng:
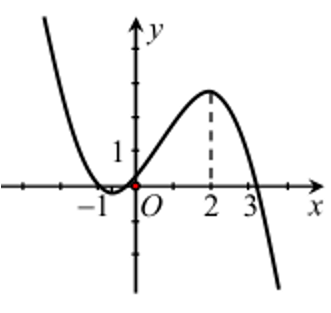
A. a < 0,b > 0,c > 0,d > 0
B. a < 0,b < 0,c < 0,d > 0
C. a < 0,b < 0,c > 0,d > 0
D. a < 0,b > 0,c < 0,d > 0
Lời giải:
Đáp án : A
Bài 1. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
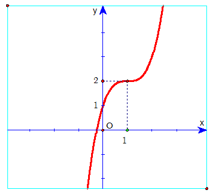
A. y = x3 – 3x + 1.
B. y = -x3 + 3x2 + 1.
C. y = x3 – 3x2 + 3x + 1.
D. y = -x3 – 3x2 – 1.
Bài 2. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
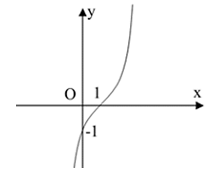
A. y = x3 – 3x2 + 3x + 1.
B. y = x3 – 3x2 – 3x – 1.
C. y = x3 – 3x2 + 3x – 1.
D. y = -x3 + 3x2 – 3x – 1.
Bài 3. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
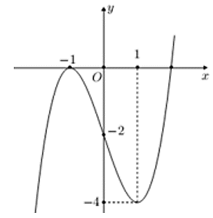
A. y = x3 – 2.
B. y = x3 – 3x – 2.
C. y = -x3 + 3x – 2.
D. y = -x3 – 3x.
Bài 4. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
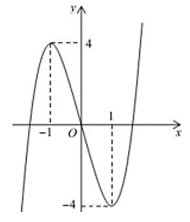
A. y = -x3 + 3x.
B. y = x3 – 3x.
C. y = 2x3 – 6x.
D. y= -2x3 + 6x.
Bài 5. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
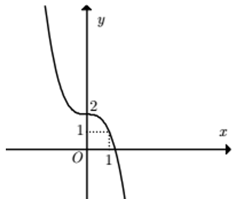
A. y = -x3 + 2.
B. y = -x3 + 3x + 2.
C. y = -x3 – x + 2.
D. y = -x3 + 1.
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn