Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q lớp 7 (cực hay, chi tiết) – Tổng hợp các dạng bài tập Toán 7 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán lớp 7.-Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q lớp 7 (cực hay, chi tiết)
Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q lớp 7 (cực hay, chi tiết)
Bài viết Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q lớp 7 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q.
Cách sử dụng kí hiệu ∈ , ∉ , ⊂ , ⊄ với các tập số N, Z, Q lớp 7 (cực hay, chi tiết)
Nắm vững ý nghĩa và kí hiệu của từng kí hiệu
+) Kí hiệu ∈ đọc là “phần tử của” hoặc “thuộc”
+) Kí hiệu ∉ đọc là “không phải là phần tử của” hoặc “không thuộc”.
+) Kí hiệu ⊂ đọc là “tập hợp con của”.
+) Kí hiệu ⊄ đọc là “không phải tập hợp con của”.
+) Kí hiệu N chỉ tập hợp các số tự nhiên.
+) Kí hiệu Z chỉ tập hợp các số nguyên.
+) Kí hiệu Q chỉ tập hợp các số hữu tỉ.
– Các kí hiệu ∈ ; ∉ dùng để so sánh giữa phần tử với tập hợp.
– Các kí hiệu ⊂ ; ⊄ dùng để so sánh giữa các tập hợp với nhau.
Ví dụ 1: Điền kí hiệu ( ∈ ; ∉ ; ⊂ ) thích hợp vào chỗ chấm
a) -10 … N -10 … Z -10 … Q
b) 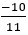 … Z
… Z 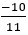 … Q
… Q 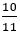 … Q
… Q
c) N … Z … Q
Lời giải:
a)
+) – 10 không phải là số tự nhiên ⇒ -10 ∉ N
+) – 10 là số nguyên âm ⇒ -10 ∈ Z
+) – 10 là số hữu tỉ vì -10 = 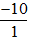 ⇒ -10 ∈ Q
⇒ -10 ∈ Q
b) Vì 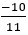 không phải là số nguyên nên
không phải là số nguyên nên 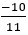 ∉ Z
∉ Z
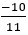 ∈ Q;
∈ Q; 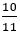 ∈ Q
∈ Q
(vì cả hai số 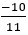 ;
; 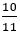 đều biểu diễn được dưới dạng
đều biểu diễn được dưới dạng 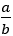 , a; b ∈ Z, b ≠ 0)
, a; b ∈ Z, b ≠ 0)
c) N ⊂ Z ⊂ Q (vì các kí hiệu N; Z; Q chỉ các tập hợp nên phải dùng kí hiệu ⊂ để so sánh).
Ví dụ 2: Điền kí hiệu N; Z; Q thích hợp vào chỗ chấm (điền tất cả các khả năng có thể)
a) 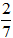 ∈ … 2 ∈ … -1008 ∈ …
∈ … 2 ∈ … -1008 ∈ …
b) Z ⊂ …
Lời giải:
a)
+) 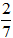 ∈ Q (vì
∈ Q (vì 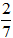 biểu diễn được dưới dạng
biểu diễn được dưới dạng 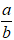 , a; b ∈ Z, b ≠ 0)
, a; b ∈ Z, b ≠ 0)
+) 2 ∈ N; 2 ∈ Z và 2 ∈ Q (vì 2 = 2/1)
+) -1008 là số nguyên âm ⇒ -1008 ∈ Z
Mặt khác: -1008 = 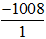 ⇒ -1008 ∈ Q
⇒ -1008 ∈ Q
b) Z là tập hợp các số nguyên, mà các số nguyên đều biểu diễn được dưới dạng a/1 (a ∈ Z), do đó các số nguyên chính là các số hữu tỉ ⇒ Z ⊂ Q
Câu 1. Điền kí hiệu ( ∈ ; ∉ ; ⊂ ; ⊄) thích hợp vào chỗ chấm:
a) 2020 … N 2020 … Z 2020 … Q
b) 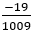 … N
… N 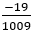 … Z
… Z 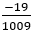 … Q
… Q
c) {0;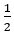 ;1} … N {0;
;1} … N {0;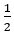 ;1} … Z {0;
;1} … Z {0;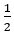 ;1} … Q
;1} … Q
Lời giải:
a) 2020 ∈ N 2020 ∈ Z 2020 ∈ Q (vì 2020 = 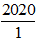 )
)
b) 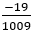 ∉ N
∉ N 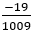 ∉ Z
∉ Z 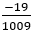 ∈ Q
∈ Q
c) {0;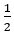 ;1} là một tập hợp, nên ta sử dụng kí hiệu ⊂ và ⊄
;1} là một tập hợp, nên ta sử dụng kí hiệu ⊂ và ⊄
0;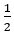 ;1 là các phần tử của tập hợp {0;
;1 là các phần tử của tập hợp {0;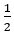 ;1}
;1}
Ta có: 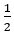 ∉ N ⇒ {0;
∉ N ⇒ {0;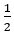 ;1} ⊄ N
;1} ⊄ N
Tương tự vì 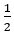 ∉ Z ⇒ {0;
∉ Z ⇒ {0;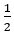 ;1} ⊄ Z
;1} ⊄ Z
Mặt khác vì 0 ∈ Q; 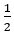 ∈ Q; 1 ∈ Q ⇒ {0;
∈ Q; 1 ∈ Q ⇒ {0;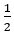 ;1} ⊂ Q
;1} ⊂ Q
Câu 2. Điền kí hiệu N; Z; Q thích hợp vào chỗ chấm (điền tất cả các khả năng có thể)
a) -2021 ∈ … 2021 ∈ …
b) 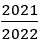 ∈ … –
∈ … – 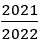 ∈ …
∈ …
Lời giải:
a) Ta có: -2021 ∈ Z; -2021 ∈ Q (vì -2021 = 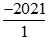 )
)
2021 ∈ N 2021 ∈ Z 2021 ∈ Q
b) 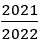 ∈ Q –
∈ Q – 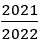 ∈ Q
∈ Q
Câu 3. Trong các câu sau, câu nào đúng, câu nào sai?
a) Số 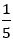 là số tự nhiên nên
là số tự nhiên nên 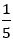 ∈ N
∈ N
b) Số 2080 là số tự nhiên nên 2080 ∈ N
c) Số 2080 không phải là số hữu tỉ nên 2080 ∉ Q
d) Số 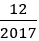 vừa là số nguyên vừa là số hữu tỉ nên
vừa là số nguyên vừa là số hữu tỉ nên 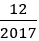 ∈ Z và
∈ Z và 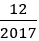 ∈ Q
∈ Q
e) Số 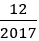 là số hữu tỉ, nhưng nó không phải số nguyên nên
là số hữu tỉ, nhưng nó không phải số nguyên nên 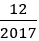 ∈ Q và
∈ Q và 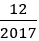 ∉ Q
∉ Q
Lời giải:
a) Số 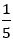 không phải số tự nhiên ⇒ a sai
không phải số tự nhiên ⇒ a sai
b) Số 2080 là số tự nhiên, nên ta sử dụng kí hiệu ∈ là đúng ⇒ b đúng
c) Vì 2080 = 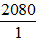 nên 2080 là số hữu tỉ ⇒ c sai
nên 2080 là số hữu tỉ ⇒ c sai
d) 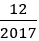 không phải là số nguyên ⇒ d sai
không phải là số nguyên ⇒ d sai
e) 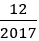 là số hữu tỉ và
là số hữu tỉ và 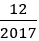 không là số nguyên ⇒ e đúng
không là số nguyên ⇒ e đúng
Câu 4. Chọn khẳng định sai trong các định sau.
A. 1200 ∈ N
B. -1200 ∈ N
C. -1200 ∈ Q
D. -1200 ∈ Z
Lời giải:
Ta có 1200 là số tự nhiên nên 1200 ∈ N, suy ra A đúng
-1200 là số nguyên âm, nó không phải là số tự nhiên nên -1200 ∉ N và -1200 ∈ Z, suy ra B sai, D đúng
-1200 = 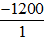 ⇒ -1200 ∈ Q, suy ra C đúng
⇒ -1200 ∈ Q, suy ra C đúng
Đáp án B
Câu 5. Chọn đáp án đúng
A. Q ⊂ N
B. Z ⊂ N
C. Q ⊂ Z
D. Z ⊂ Q
Lời giải:
Nhắc lại khái niệm tập hợp con: Cho A và B là hai tập hợp. Khi đó nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta gọi tập hợp A là tập hợp con của tập hợp
B.
+) Ta thấy: 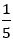 ∈ Q nhưng
∈ Q nhưng 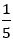 ∉ N, vậy tập hợp Q không phải là tập hợp con của tập hợp N, suy ra đáp án A sai.
∉ N, vậy tập hợp Q không phải là tập hợp con của tập hợp N, suy ra đáp án A sai.
+) Lấy phần tử -2, ta thấy -2 ∈ Z nhưng -2 ∉ N nên tập hợp Z không phải là tập hợp con của tập hợp N, suy ra đáp án B sai.
+) Ta thấy 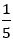 ∈ Q nhưng
∈ Q nhưng 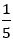 ∉ Z vậy tập hợp Q không phải là tập hợp con của tập hợp Z
∉ Z vậy tập hợp Q không phải là tập hợp con của tập hợp Z
Suy ra đáp án C sai.
+) Vì mọi số nguyên a đều viết được dưới dạng 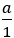 với a ∈ Z nên mọi số nguyên đều là số hữu tỉ. Vậy Z ⊂ Q.
với a ∈ Z nên mọi số nguyên đều là số hữu tỉ. Vậy Z ⊂ Q.
Đáp án D
Bài 1. Điền kí hiệu thích hợp vào chỗ trống:
a) −35…ℤ; −35∈….
b) ℕ … ℤ ⸦ ….
Bài 2. Khẳng định nào dưới đây là sai?
A. ℕ ⸦ ℤ ⸦ ℚ;
B. −47 ∈ ℚ;
C. −47 ∈ ℤ;
D. 23∉ℤ.
Bài 3. Điền kí hiệu ℕ; ℤ; ℚ thích hợp vào chỗ chấm (điền tất cả các khả năng có thể)
a) 12023∈…;
b) −20242023∈…;
c) 2024 ∈ …
Bài 4. Cho các tập hợp: A = {3; 4; 5; 6; 7}; B = { x ∈ ℕ*| x ≤ 4}
a) Viết tập hợp A dưới dạng tính chất đặc trưng, tập hợp B dưới dạng liệt kê?
b) Tìm C = A ∪ B và D = A∩B .
c) Tập hợp M = { x ∈ ℕ*| 4< x ≤ 6} có quan hệ gì với tập hợp A?
Bài 5. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Sô −1 là một số tự nhiên nên ta có −1 ∈ ℕ;
b) Số 2024 là một số tự nhiên nên ta có 2024 ∈ ℕ;
c) Số 20232024 vừa là số nguyên vừa là số hữu tỉ nên 20232024∈ℤ ; 20232024∈ℚ.
Xem thêm các dạng bài tập Toán lớp 7 chọn lọc, có đáp án hay khác:
Lời giải bài tập lớp 7 sách mới:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn