Cách tìm ước chung và bội chung lớp 6 (nhanh nhất, cực hay) – Tổng hợp các dạng bài tập Toán lớp 6 với phương pháp giải chi tiết giúp bạn biết cách làm bài tập Toán 6.-Cách tìm ước chung và bội chung lớp 6 (nhanh nhất, cực hay)
Cách tìm ước chung và bội chung lớp 6 (nhanh nhất, cực hay)
Bài viết Cách tìm ước chung và bội chung lớp 6 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách tìm ước chung và bội chung.
Cách tìm ước chung và bội chung lớp 6 (nhanh nhất, cực hay)
1. Ước Chung
Định nghĩa 1: Cho hai số a và b. Nếu có một số d thoả mãn a ⋮ d và b ⋮ d thì d được gọi là ước chung của a và b.
Tập hợp các ước chung của hai số a và b được kí hiệu là ƯC(a,b).
Chú ý: ta cần chú ý tới:
Nếu x ∈ ƯC(a, b, c,…) thì a ⋮ x, b ⋮ x,c ⋮ x,…
Nếu ƯC(a, b) = 1 thì a và b được gọi là hai số nguyên tố cùng nhau
Kí hiệu (a, b) = 1
ƯC(a, b) = Ư(a) ∩ Ư(b)
Ta có hai nhận xét sau:
Nếu số a chia hết cho m và n mà m, n là hai nguyên tố cùng nhau thì a chia hết cho tích m.n, cụ thể:
a ⋮ m,a ⋮ n và (m,n)=1 ⇒ a ⋮ m.n
Nếu tích a.b ⋮ m mà b và m là hai số nguyên tố cùng nhau thì a phải chia hết cho m, cụ thể:
a. b ⋮ m và (b, m) = 1 ⇒ a ⋮ m
2. Bội Chung
Định nghĩa 2: Cho hai số a và b. Nếu có một số d thoả mãn d ⋮ a và d ⋮ b thì d được gọi là bội chung của a và b.
Tập hợp các bội chung của hai số a và b được kí hiệu là BC(a, b).
Chú ý: Ta cần chú ý tới:
Nếu x ∈ BC(a,b,c,…) thì x ⋮ a,x ⋮ b,x ⋮ c,…
BC(a, b) = B(a) ∩ B(b)
Ví dụ 1: Cho ba số a = 15, b=80,c=120
a) Tìm tập hợp các ước của a, b, c.
b) Tìm tập hợp các ước chung của a và b; b và c; a,b và c
Lời giải:
a) Ta có:
Ư(15)= {1,3,5,15}
Ư(80)= {1,2,4,5,8,10,16,20,40,80}
Ư(120)= {1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120}
b) Ta có
ƯC(15,80)= {1,5}
ƯC(80,120)= {1,2,4,5,8,10,20,40}
ƯC(15,80,120)= {1,5}
Ví dụ 2:
a) Tìm năm số tự nhiên sao cho khi chia cho 5,7,11 đều dư 4.
b) Tìm hai số tự nhiên sao cho khi chia cho 3,7,15 đều dư 1
Lời giải:
a) Gọi x là số tự nhiên khi chia cho 5,7,11 đều dư 4.
Ta có x ∈ BC(5,7,11)+4
Lại có:BC(5,7,11) = {385,770,1155,1540,1925,…..}
Vậy, ta được x ∈ X = {389,774,1159,1544,1929}
b) Gọi x là số tự nhiên khi chia cho 3,7,15 đều dư 1.
Ta có x ∈ BC(3,7,15)+1
Lại có:BC(3,7,15) = {105,210,315,….}
Vậy, ta được x ∈ X = {106,211}
Ví dụ 3: Tìm số tự nhiên a. Biết số đó chia hết cho 7 và khi chia cho 2, cho 3, cho 4, cho 5, cho 6 đều dư 1 và a nhỏ hơn 400
Giải
Lời giải:
Ta có:
a-1 ∈ BC(2,3,4,5,6) → a-1 ∈ {60,120,180,240,300,360}
→ a ∈ {61,121,181,241,301,361}
Do a ⋮ 7 nên a = 301
Vậy, ta tìm được a = 301
Ví dụ 4: Tìm giao của hai tập hợp sau
a. A = {1;2;3;4;5;6;7} B = {3;4;5;6;7;8;9}
b. C = {cam; chanh;táo} D = {chanh; nho}
c. E = {1;3;5;7;9} G = {2;4;6;8}
Lời giải:
a. A ∩ B = {3;4;5;6;7}
b. C ∩ D = {Chanh}
c. E ∩ G = ∅
Câu 1: Tìm tập hợp các bội chung của 15 và 18 nhỏ hơn 200
A. A={0;45;90;120}
B. A={0;45;90;120;180}
C. A={0;90;80}
D. A={0;60;90;120}
Lời giải:
Đáp án: C
A. A={0;45;90;120} Sai
B. A={0;45;90;120;180} → Sai
C. A={0;90;80} → Đúng
D. A={0;60;90;120} → Sai vì 60 không chia hết cho 18
Câu 2: Tập hợp ƯC(4, 12) là:
A. {0;1;2;4}
B. {1;2;4}
C. {1;2;3;4}
D. {1;2;3;4;6}
Lời giải:
Đáp án: B
Tập hợp ƯC(4, 12) là:
A. {0;1;2;4} → Sai vì 0 không là ước của mọi số
B. {1;2;4} → Đúng
C. {1;2;3;4} → Sai vì 3∉ Ư(4)
D. {1;2;3;4;6} → Sai vì 6∉ Ư(4)
Câu 3: Cho tập hợp A gồm các bội của 8, tập hợp B gồm các bội của 100, tập hợp C gồm các bội chung của 8 và 100. Hãy nêu mối quan hệ giữa tập hợp C với hai tập hợp A và B.
A. C⊂A,C⊂B
B. A⊂C,B⊂C
C. C⊂A,B⊂C
D. A⊂C,C⊂B
Lời giải:
Đáp án: A
Ta có: C ⊂ A,C ⊂ B
Câu 4: Tìm giao của hai tập hợp A và B, biết rằng A = {vở; bút; thước; tẩy} B = {vở; sách; cặp; thước; tẩy}
A. C={vở; sách; tẩy}
B. C={vở; bút; sách; tẩy}
C. C={vở; thước; tẩy}
D. C={vở; sách; cặp}
Lời giải:
Đáp án: C
A ∩ B = {Vở; thước; tẩy}
Câu 5: Liệt kê các phần tử của tập hợp A = ƯC{20; 30}
A. A={1; 2; 4; 10}
B. A={1; 2; 5;10; 15}
C. A={1; 2; 5}
D. A={1; 2; 5;10}
Lời giải:
Đáp án: D
A = ƯC(20;30)
Ư(20) = {1;2;4;5;10;20}
Ư(30) = {1;2;3;5;6;10;15;30}
A = ƯC(20;30) = {1;2;5;10}
Câu 6: Số x là ước chung của số a và số b nếu:
A. x ∈ Ư(a) và x ∈ B(b)
B. x ⊂ Ư(a) và x ⊂ Ư(b)
C. x ∈ Ư(a) và x ∈ Ư(b)
D. x ∉ Ư(a) và x ∉ Ư(b)
Lời giải:
Đáp án: C
x ∈ ƯC (a,b)
⇒ x ∈ Ư(a) và x ∈Ư(b)
Câu 7: Số x gọi là bội chung của a, b, c nếu:
A. x ⋮ a hoặc x ⋮ b hoặc x ⋮ c
B. x ⋮ a và x ⋮ b
C. x ⋮ b và x ⋮ c
D. x ⋮ a và x ⋮ b và x ⋮ c
Lời giải:
Đáp án: D
x ∈ BC(a,b,c)
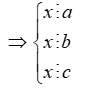
Câu 8: Tìm ước chung của 9 và 15
A. {1; 3}
B. {0; 3}
C. {1; 5}
D. {1; 3; 9}
Lời giải:
Đáp án: A
Ư(9) = {1;3;9}
Ư(15) ={1;3;5;15}
→ ƯC(9,15) = {1;3}
Câu 9: Viết các tập hợp Ư(6), Ư(20), ƯC(6, 20)
A. Ư(6) = {1; 2; 3; 6}; Ư(20) = {1; 2; 4; 5; 10; 20}; ƯC(6, 20) = {1; 2}
B. Ư(6) = {1; 2; 3; 6}; Ư(20) = {1; 2; 4; 5; 20}; ƯC(6, 20) = {1; 2}
C. Ư(6) = {1; 2; 3}; Ư(20) = {1; 2; 4; 5; 10; 20}; ƯC(6, 20) = {1; 2}
D. Ư(6) = {1; 2; 4; 6}; Ư(20) = {1; 2; 4; 20}; ƯC(6, 20) = {1; 2; 4}
Lời giải:
Đáp án: A
Ư(6) = {1; 2; 3; 6}
Ư(20) = {1; 2; 4; 5; 10; 20}
→ ƯC(6, 20) = {1; 2}
Câu 10: Chọn câu trả lời sai
A. 5 ∈ ƯC(55; 110)
B. 24 ∈ BC(3; 4)
C. 10 ∉ ƯC(55; 110)
D. 12 ⊂ BC(3; 4)
Lời giải:
Đáp án: D

Xem thêm các dạng bài tập Toán lớp 6 chọn lọc, có đáp án chi tiết hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 6 hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn