Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác cực hay – Phương pháp giải các dạng bài tập Toán 11 chi tiết giúp học sinh biết cách làm bài tập Toán 11.-Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác cực hay
Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác cực hay
Bài viết Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập
Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác.
Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác cực hay
a. Tính tuần hoàn và chu kì:
Định nghĩa: Hàm số y = f(x) có tập xác định được gọi là hàm số tuần hoàn, nếu tồn tại một số T≠0 sao cho với mọi x ∈ D ta có:
♦ (x- T) ∈ D và (x + T) ∈ D
♦ f (x + T) = f(x).
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó. Người ta chứng minh được rằng hàm số y = sinx tuần hoàn với chu kì T = 2 π ; hàm số y = cosx tuần hoàn với chu kì T = 2 π; hàm số y = tanx tuần hoàn với chu kì T = π; hàm số y = cotx tuần hoàn với chu kì T = π
Chú ý:
Hàm số y = sin(ax + b) tuần hoàn với chu kì T = 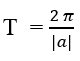
Hàm số y = cos(ax + b) tuần hoàn với chu kì T = 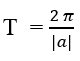
Hàm số y = tan(ax + b) tuần hoàn với chu kì T = 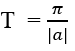
Hàm số y = cot(ax + b) tuần hoàn với chu kì T = 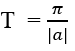
Hàm số y = f1(x) tuần hoàn với chu kì T1 và hàm số y = f2(x) tuần hoàn với chu kì T2 thì hàm số y = f1(x) ± f2(x) tuần hoàn với chu kì T0 là bội chung nhỏ nhất của T1 và T2 .
b. Hàm số chẵn, lẻ:
Định nghĩa:
Hàm số y = f(x) có tập xác định là D được gọi là hàm số chẵn nếu:
♦ x ∈ D và – x ∈ D.
♦ f(x) = f(-x).
Hàm số y = f(x) có tập xác định là D được gọi là hàm số lẻ nếu:
♦ x ∈ D và – x ∈ D.
♦ f(x) = – f(-x).
Bài 1: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau:
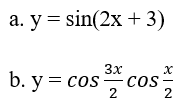
Hướng dẫn giải
a. Hàm số đã cho tuần hoàn với chu kì T = 2π/2 = π.
b.
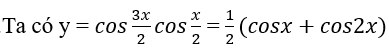
Ta có hàm số y = cosx tuần hoàn với chu kì T = 2 π , hàm số y = cos2x tuần hoàn với chu kì T = π. Vậy hàm số đã cho tuần hoàn với chu kì T = 2 π .
Bài 2: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau: y = cosx + cos√3x.
Hướng dẫn giải
Giả sử hàm số đã cho tuần hoàn với chu kì T ≠ 0. Khi đó ta có:
cos(x + T) + cos[√3(x +T)] = cosx + cos√3x.
Cho x = 0. Ta có: cosT + cos√3T = 2. Vì cosx ≤ 1 với mọi x nên ta có:
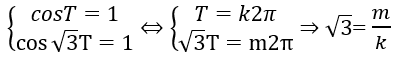
mà m, k ∈ Z (vô lý). Vậy hàm số đã cho không tuần hoàn.
Bài 3: Xét tính chẵn lẻ của các hàm số sau:
a. y = sinx.
b. y = cos(2x).
c. y = tanx + cos(2x + 1).
Hướng dẫn giải
a. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: sin (-x) = -sinx. Vậy hàm số đã cho là hàm số lẻ.
b. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: cos(-2x) = cos(2x). Vậy hàm số đã cho là hàm số chẵn.
c.
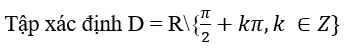
Lấy x ∈ D thì – x ∈ D. Ta có:
tan(-x) + cos(-2x + 1) = -tanx + cos(-2x + 1).
Vậy hàm số đã cho không chẵn, không lẻ.
Bài 1: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau:
a) y = cos(-2x +4)
b) y = tan(7x + 5)
Lời giải:
a) Hàm số đã cho làm hàm tuần hoàn với chu kì T = 2π/2 = π
b) Hàm số đã cho làm hàm tuần hoàn với chu kì T =π /7.
Bài 2: Xét tính tuần hoàn và tìm chu kì cơ sở của hàm số sau: y = sinx + sin3x
Lời giải:
Ta có y = sinx là hàm tuần hoàn với chu kì T = 2 π và hàm số y = sin3x là hàm tuần hoàn với chu kì T = (2 π)/3. Vậy hàm số đã cho là hàm tuần hoàn với chu kì T = 2 π .
Bài 3: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau: y = cosx + 2sin5x
Lời giải:
Làm tương tự bài 2 và sử dụng chú ý phần tính tuần hoàn và chu kì, ta có hàm số đã cho là hàm tuần hoàn với chu kì T = 2 π .
Bài 4: Xét tính chẵn, lẻ của các hàm số sau:
a) y = cosx + cos2x
b) y = tanx + cotx.
Lời giải:
a) Ta có tập xác định của hàm số là D = R.
cos(-x) + cos(-2x) = cosx + cos2x. Vậy hàm số đã cho là hàm số chẵn.
b) Ta có tập xác định của hàm số là D = R{k π/2, k ∈ Z}.
tan(-x) + cot(-x) = – tanx – cotx. Vậy hàm số đã cho là hàm số lẻ.
Bài 5: Xét tính chẵn, lẻ của các hàm số sau:
a) y = cosx + sinx.
b) y = sin2x + cot100x
Lời giải:
a) Ta có tập xác định của hàm số là D = R.
sin (-x) + cos(-x) = – sinx + cosx. Vậy hàm số đã cho là hàm không chẵn, không lẻ.
b) Ta có tập xác định của hàm số là D = R{k π /100, k ∈ Z}.
sin(-2x) + cot(-100x) = – sin2x – cot(100x). Vậy hàm số đã cho là hàm số lẻ.
Bài 1. Xét tính chẵn lẻ của hàm số: f(x) = 2sinx−3tanx3+cosx.
Bài 2. Xét tính chẵn lẻ của hàm số: y = 2sin2x + 3cosx.
Bài 3. Xét tính chẵn lẻ của hàm số: y = 3cos2x + 2sinx.
Bài 4. Xét tính chẵn lẻ của hàm số: y = sin3x.
Bài 5. Xét tính chẵn lẻ của các hàm số sau:
a) y = 5sin2x + 2tan x;
b) y = cos3x + 1sin3x;
c) y = sin5x.cos2x;
d) y = sin22x.
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:

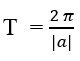
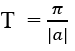

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn